问题描述
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量。说明:你不能倾斜容器。
解析
这题的暴力方法实际上很容易想到,对每个元素进行二重遍历或者找到最高的长度进行二重遍历,时间复杂度分别是O(m^2)以及O(m*n)。实际上可以使用双指针降低时间复杂度。主要原理就是,左右两边谁低,那么那边的指针向内移动,移动后容积一定比另一边向内移动后的容积要大,因为移动高的h1最多减少h1的容积(可能增加),但移动低的h2最多减少h2的容积。
public int maxArea(int[] height) {
int left = 0, right = height.length - 1;
int maxSize = 0;
while(left < right){
boolean leftBigger = height[left] > height[right];
int min = leftBigger ? height[right] : height[left];
int current = (right - left) * min;
if(current > maxSize){
maxSize = current;
}
if(leftBigger){
right --;
}
else{
left ++;
}
}
return maxSize;
}
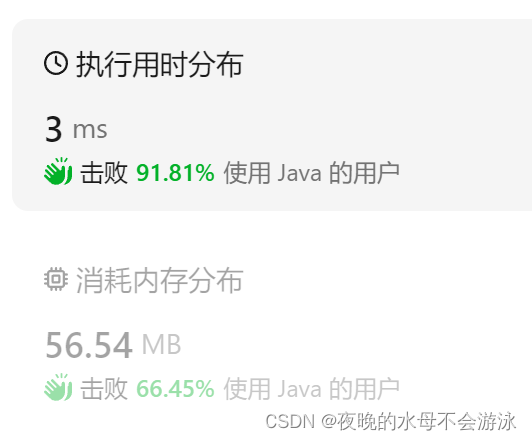
实际上代码还可以优化,由于都是整形数据,那么只要比较,那么最小也是小1,而每次移动造成的容积变化都是H*1,因此只要比较H即可,当H<当前的最小值的时候 ,小的值一定是大于1的,因此可以直接继续移动指针。
public int maxArea(int[] height) {
int left = 0, right = height.length - 1;
int maxSize = 0;
while(left < right){
int min = height[left] > height[right] ? height[right] : height[left];
int current = (right - left) * min;
if(current > maxSize){
maxSize = current;
}
while (height[left] <= min && left < right) {
left++;
}
while (height[right] <= min && left < right) {
right--;
}
}
return maxSize;
}
```