一、摊还分析
概念:是求数据结构中一个操作序列执行所有操作的平均时间,与平均复杂度不同,它不涉及输入概率,能够保证在最坏情况下操作的平均性能。
适用场景:用含 n 个操作的序列(o1,o2,,,,,on) 维护某数据结构
操作代价:单次操作代价可能会很大,在最坏情况下代价为 max(oi)
二、摊还分析的三种方法
以栈的操作为例,说明摊还分析的三种方法
栈操作
基本原则:先进后出
基本操作:
① POP(S):将栈 S 的栈顶对象弹出,并返回该对象 代价为O(1)
② PUSH(S,x):将对象 x 压入栈 S 中 代价为O(1)
(一个含有n个PUSH和POP操作的序列的总代价为n,n个操作的实际运行时间为O(n))
③ MULTIPOP(S,k):弹出栈 S 的栈顶 k 个对象 代价为 O( min(s,k) )
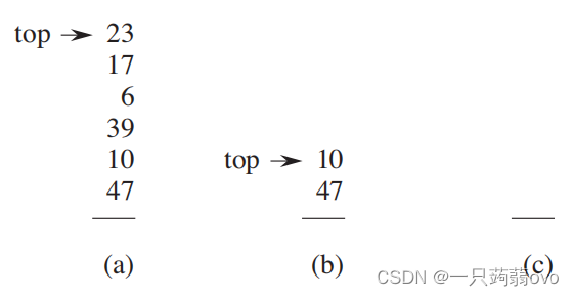
1.聚合分析
如果对所有的 n ,一个 n 个操作的序列最坏情况下花费的总时间为T(n),那么在最坏情况下,每个操作的平均代价,或摊还代价为 T(n) / n 。此外,摊还代价是适用于每个操作的,即使序列中有多种类型的操作也是如此。
假设栈的大小最大为 n ,则执行MULTIPOP操作的最坏情况是 O(n),因此,一个 n 个操作的序列的最坏情况为 ,操作序列包含了 n 个MULTIPOP操作(n*n)。
然而,考虑整个序列的 n 个操作,PUSH 和 POP 的代价为1,最坏的情况下,一定是前 n-1次操作都是 PUSH,最后一次 MULTIPOP(S,n-1),此时的代价为 2*(n-1)=2*n-2,时间复杂度为 O(n),平均每个操作的摊还代价为 O(1)
2.核算法
对于不同操作赋予不同费用,某些操作的费用可能多于或少于其实际代价。 赋予一个操作的费用,称为它的摊还代价。 当一个操作的摊还代价超出其实际代价时,差额部分存入数据结构中的特定对象,存入的差额称为信用。 对于后续操作中摊还代价小于实际代价的情况,信用可以用于支付差额。 需要确保操作序列的总摊还代价是序列总真实代价的上界。
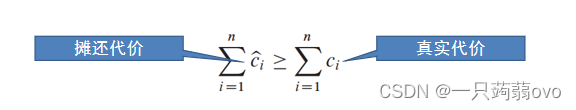
同样,对于栈操作,赋予其费用(如图)
PUSH操作的摊还代价为 2 ,相当于进栈时的代价1 + 压入对象出栈的代价1,此时POP和MULTIPOP操作的摊还代价为 0,对于一个n个操作序列,最坏的情况就是 n 个PUSH操作,此时代价为 2n,时间复杂度为 O(n)。
3.势能法
与核算法相似,势能法摊还分析并不将预付代价表示为特定对象的信用,而是表示成“势能”,将势能释放即可用来支付未来操作的代价。
摊余成本 = 真实开销 + 新势能 – 旧势能
假设 n 个操作将数据结构从 D0 修改为 D1 直至…Dn.
令 Φ(D) 代表数据结构 D 的势.
令 ci 代表第 i 个操作的真实代价. 令 ĉi 代表第 i 个操作的摊还代价.

对于势能的理解,若,则操作 i 在数据结构中存入能量以便以后使用
若,则数据结构为操作 i 提供能量执行
根据累加有:
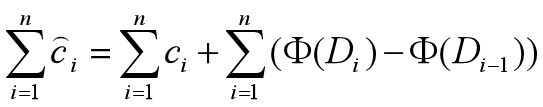

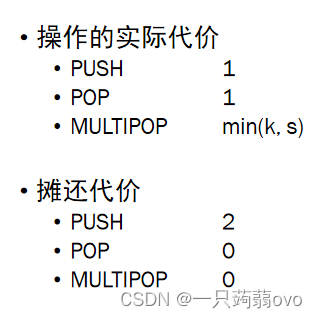
总摊还代价是总实际代价的一个上界
栈操作:
将栈的势函数定义为其中的对象数量,对于其实空栈D0,有 Φ(D0)=0
因此第 i 步操作得到的栈具有非负的势 Φ(Di) >= 0 = Φ(D0),则用Φ定义的n个操作的总摊还代价是实际代价的上界。
假定PUSH ,POP操作的代价为1,MULTIPOP操作的代价为 k,且规定压入栈一个对象势能+1,弹栈一个对象势能-1。
如果第 i 个操作是PUSH操作,且栈中有 s 个对象
势差为: Φ(Di)-Φ(Di-1) = (s + 1) – s = 1
摊还代价是: ĉi=ci+ Φ(Di) - Φ(Di-1) = 1+1 = 2 (核算法)
三、动态表中插入操作代价的摊还分析
当动态表中空间不足时,申请更多内存增大动态表中的空间,并重新插入旧元素。
插入元素操作的思路:当空间不足时,将动态表中的内存*2,并且将所有旧元素插入至新的动态表中。插入开销为:

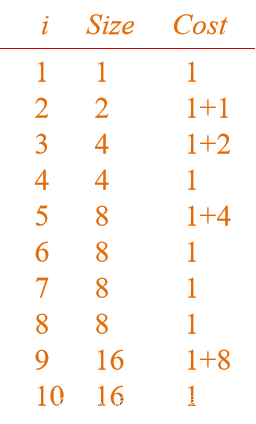
1.聚合分析:
根据上述 Ci 的值,将所有代价相加求和:
总代价为T(n)= ,为 O(n),摊还代价为 O(1)
2.核算法
第 i 次插入支付费用为 3 (包含此次插入的开销1+重新插入元素1+重新插入旧元素1)
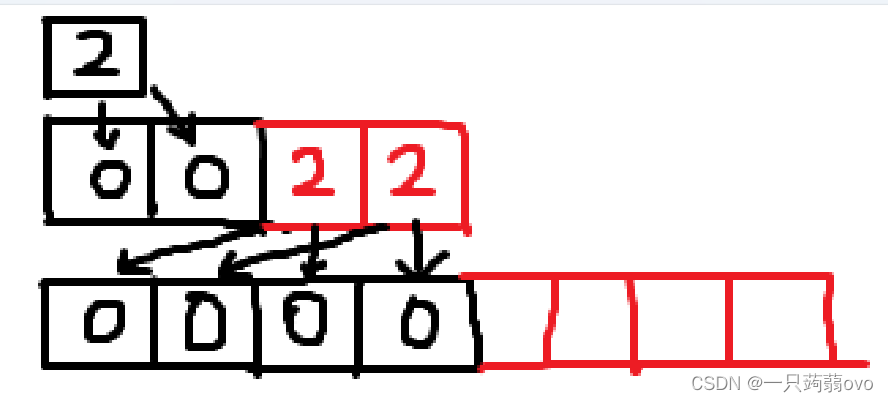

则对于一个含有n个操作的序列总代价为 3n,时间复杂度为 O (n),每个操作的摊还代价为O(1)
3.势能法
定义势函数为: Φ(T)=2 * T.num – T.size(T.num为动态表中元素个数,T.size为动态表容量)
①一次扩张后: T.size=2*(T.num-1),Φ(T)=0 (扩张后 T.num-1 为 2 的幂)
②扩张前: T.num=T.size Φ(T)=T.num (扩张前 T.num 为 2 的幂)
未触发动态表扩张
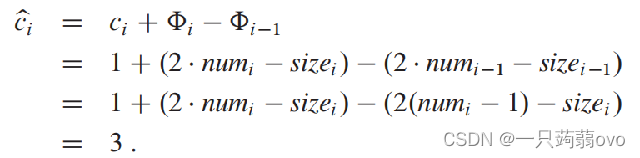
触发动态表扩张
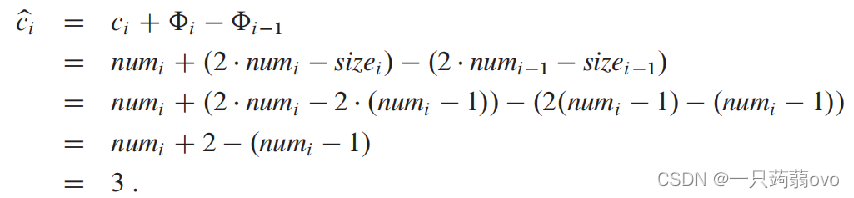
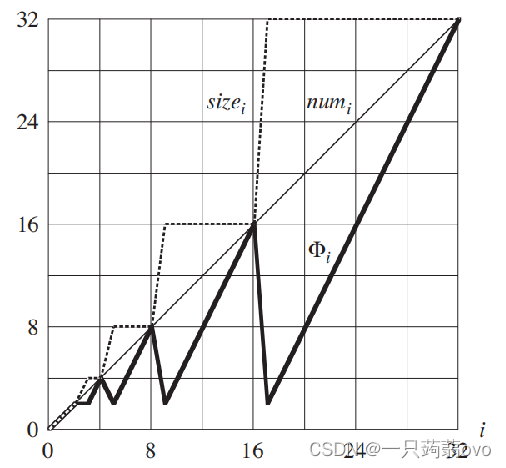
4.关于动态表的插入与删除的思考
对于动态表中的元素,可能增加,也可能减少,总是维护大表浪费空间,同时支持元素插入和删除操作。
动态表空间想法:
① 当表溢出时,将表的空间增大一倍
② 当表不足 1/2 满时,将表的空间缩减一半。
出现性能不佳:在表满的时候,持续执行插入 删除 插入 删除 插入等操作,此时会不断的扩张和缩减容量。 -------> 将②中 1/2 改为 1/4,可以适当减少此情况的发生
势能法分析:

插入元素时:
情况一: αi-1 >= 1/2 上述势能法已有
情况二: αi-1 < 1/2, 且αi < 1/2
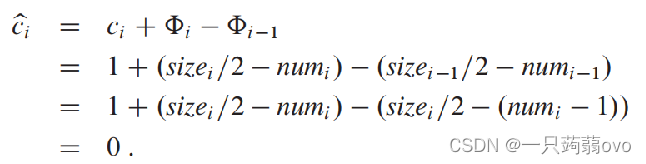
情况三: αi-1 < 1/2, 且αi >= 1/2
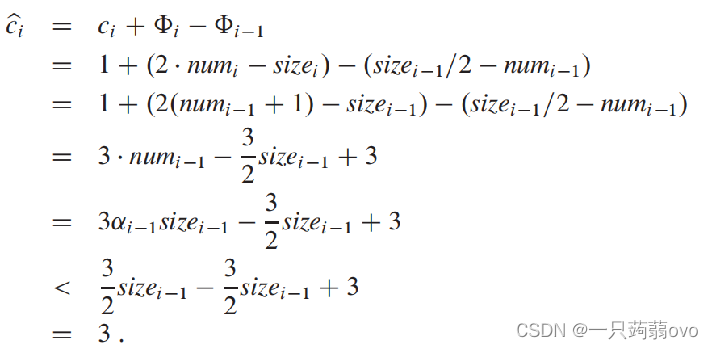
删除元素时:
情况一:αi-1 >= 1/2 上述势能法已有
情况二:αi-1 < 1/2, 且未收缩
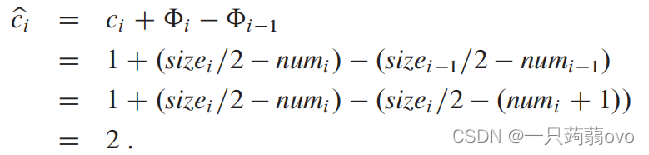
情况三: αi-1 < 1/2, 且收缩 ( size[i]=2*(num[i]+1) size[i]*2=size[i-1] ) 容量仍减半(非1/4)
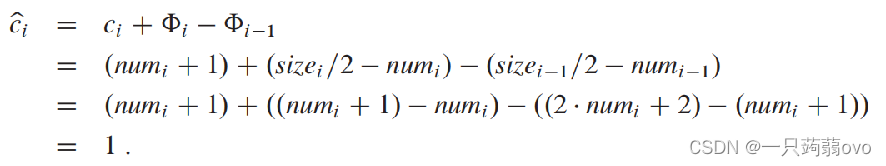
势能变化:
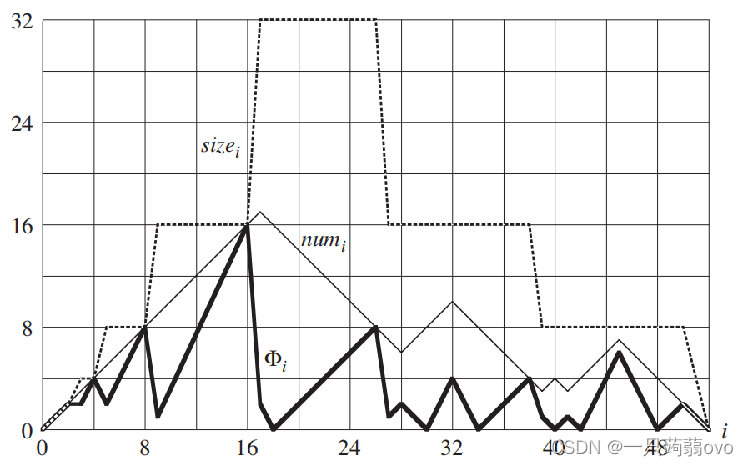
每个操作的摊还代价的上界都是一个常数。因此,在一个动态表上执行任意n个操作的实际运行时间是O(n)