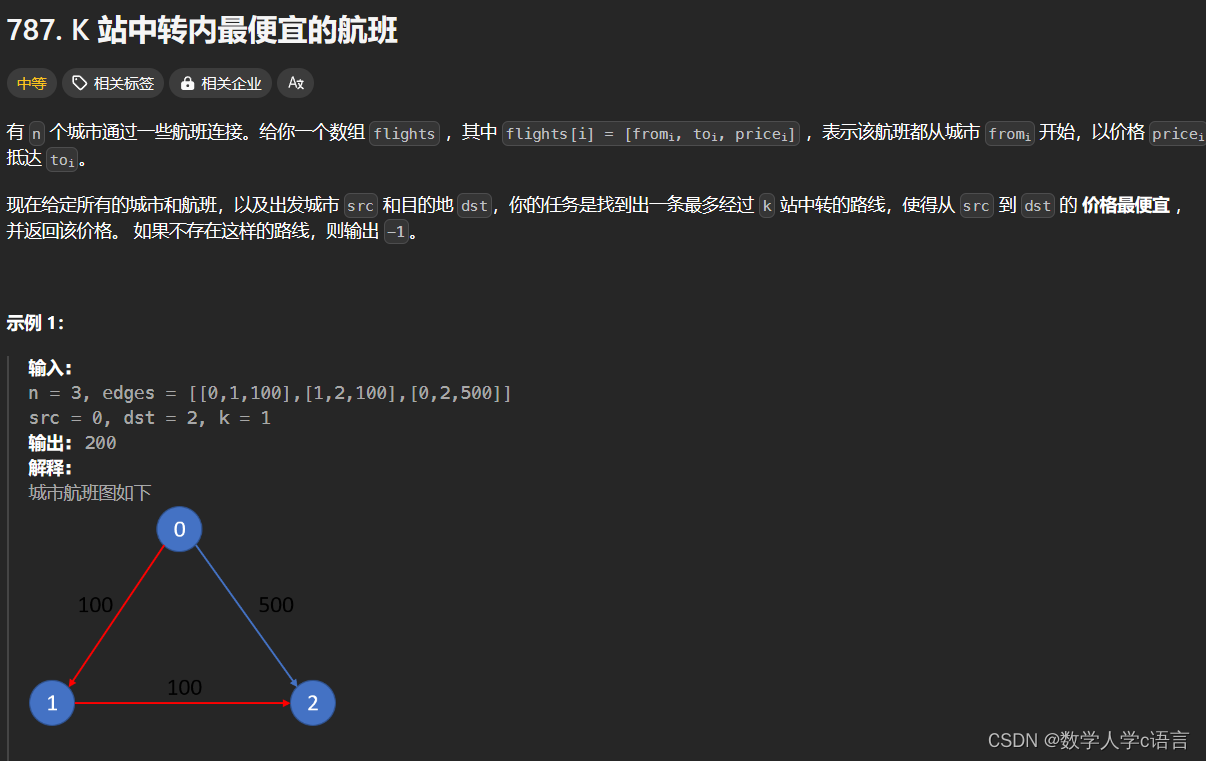
 开始准备用dfs深度搜索,发现n=100,dfs可能会超时,即使用了剪枝。
开始准备用dfs深度搜索,发现n=100,dfs可能会超时,即使用了剪枝。
class Solution:
def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, k: int) -> int:
length = k + 2
ans = float('inf')
rec = []
vis = [True]*n
edge = defaultdict(list)
for f, t, p in flights:
edge[f].append([t, p])
def dfs(node, spend):
nonlocal ans
rec.append(node)
vis[node] = False
if node == dst:
ans = min(ans, spend)
elif len(rec) < length:
for nex, p in edge[node]:
if not vis[nex]: continue
dfs(nex, spend + p)
rec.pop()
vis[node] = True
dfs(src, 0)
return ans if ans != float('inf') else -1理所当然的想用bfs,n=100肯定不会超时,谁知道题目针对,这次内存超了。因为题目中
0 <= flights.length <= (n * (n - 1) / 2)
相当于100*99/2,大概5000条路线呗。这就超了???
class Solution:
def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, k: int) -> int:
edge = defaultdict(dict)
for f, t, p in flights:
edge[f][t] = p
qu = deque()
ans = float('inf')
qu.append([src, 0, -1])
while qu:
node, spend, num = qu.popleft()
if num > k:continue
if node == dst:
ans = min( ans, spend )
continue
for nex in edge[node]:
qu.append([nex, spend + edge[node][nex], num + 1])
return ans if ans != float('inf') else -1看见大佬的优化过程,叹为观止。
使用最小堆,每次弹出列表中最小花费的路径,利用steps避免走成一个环。发现我之前的问题,应该就是走进一个环中,导致数据增多,内存超了。
import heapq as pq
class Solution:
def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, k: int) -> int:
edge = defaultdict(dict)
for f, t, p in flights:
edge[f][t] = p
qu = [[0, src, -1]]
pq.heapify(qu)
steps = [k+1]*n
while qu:
spend, node, num = pq.heappop(qu)
if steps[node] <= num:continue
steps[node] = num
if node == dst:
return spend
for nex in edge[node]:
pq.heappush(qu, [spend + edge[node][nex], nex, num + 1])
return -1
下面是官方题解,使用dp。
使用dp动态规划算法,设dp【t】【i】,表示转到第t站,从src到达i所需的最小花费数;
那么dp【t】【i】 = min(dp【t】【i】,dp【t-1】【j】+cost【j】【i】),遍历所有路线。
class Solution:
def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, k: int) -> int:
dp = [[float('inf')]*(n) for _ in range(k+2)]
dp[0][src] = 0
ans = float('inf')
for t in range(1, k+2):
for j, i, p in flights:
dp[t][i] = min(dp[t][i], dp[t-1][j] + p)
if i == dst: ans = min (ans, dp[t][i])
return ans if ans != float('inf') else -1这个动态规划,内核也就是bfs。第一次只更新了从src出发到达的节点。这个方法稍稍不如bfs,因为每一步都走了一些不能走的点。