---

📋 前言

在当今工业领域，图思维方式与图数据技术的应用日益广泛，成为图数据探索、挖掘与应用的坚实基础。本文旨在分享嬴图团队在算法实践应用中的宝贵经验与深刻思考，不仅促进业界爱好者之间的交流，更期望从技术层面为企业在图数据库选型时提供新的视角与思路。

---

🎯 K邻算法的实践意义

K邻算法（K-Hop Neighbor），即K跳邻居算法，是一种基于广度优先搜索（BFS）的遍历策略，用于探索起始节点周围的邻域。该算法在关系发现、影响力预测、好友推荐等预测类场景中得到了广泛应用。

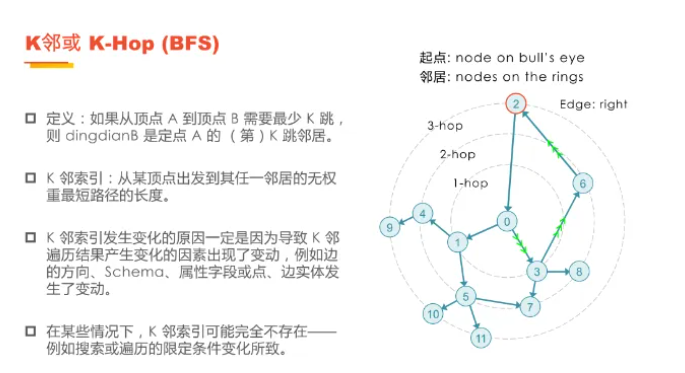
在图论中，沿着一条边移动被视为一跳（hop）。在遍历图中的顶点时，我们需要考虑多跳问题。图论起源于数学家欧拉在1836年提出的哥尼斯堡七桥问题，它奠定了图计算的数学基础。自20世纪80年代以来，图计算技术迅速发展，成为现代计算领域的重要组成部分。

在现实世界中，危机的传播正是K邻搜索的一个典型应用。以发生危机的实体为起点，顺着或逆着（取决于边的具体定义）边的方向进行1步、2步、3步乃至更深层次的查询，得到的就是先后会被危机波及到的实体。

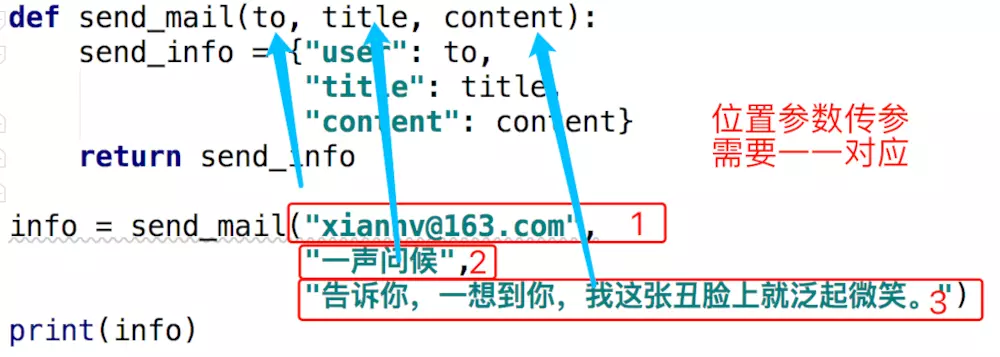
以下是一个简单的 JavaScript 示例，演示了如何使用K邻近（K-Nearest Neighbors，KNN）算法进行分类。在这个示例中，我们将创建一个简单的数据集，包含两个特征（x和y坐标）和两个类别（0和1），然后使用KNN算法对新数据进行分类。

// 定义数据集
const dataset = [
  { x: 1, y: 2, label: 0 },
  { x: 2, y: 3, label: 0 },
  { x: 3, y: 4, label: 0 },
  { x: 4, y: 5, label: 1 },
  { x: 5, y: 6, label: 1 }
];

// 定义一个函数来计算两点之间的欧氏距离
function euclideanDistance(point1, point2) {
  const dx = point1.x - point2.x;
  const dy = point1.y - point2.y;
  return Math.sqrt(dx * dx + dy * dy);
}

// 定义KNN分类函数
function knn(dataset, newPoint, k) {
  // 计算新数据点到数据集中每个点的距离
  const distances = dataset.map(data => ({
    point: data,
    distance: euclideanDistance(newPoint, data)
  }));

  // 根据距离排序数据点
  distances.sort((a, b) => a.distance - b.distance);

  // 取前k个最近的点
  const nearestNeighbors = distances.slice(0, k);

  // 统计最近邻居中各类别的数量
  const counts = nearestNeighbors.reduce((acc, curr) => {
    const label = curr.point.label;
    acc[label] = (acc[label] || 0) + 1;
    return acc;
  }, {});

  // 找到最多的类别
  let maxCount = 0;
  let predictedLabel;
  for (const label in counts) {
    if (counts[label] > maxCount) {
      maxCount = counts[label];
      predictedLabel = label;
    }
  }

  return predictedLabel;
}

// 测试新数据点的分类
const newPoint = { x: 3.5, y: 4.5 };
const k = 3;
const predictedLabel = knn(dataset, newPoint, k);
console.log(`新数据点 (${newPoint.x}, ${newPoint.y}) 的预测类别是：${predictedLabel}`);

🎯 创新应用与案例分析

以某知名房地产企业HD的供应链图谱为例，我们可以通过持股方向、资金流向等信息，清晰直观地揭示危机的传播路径和传递对象。

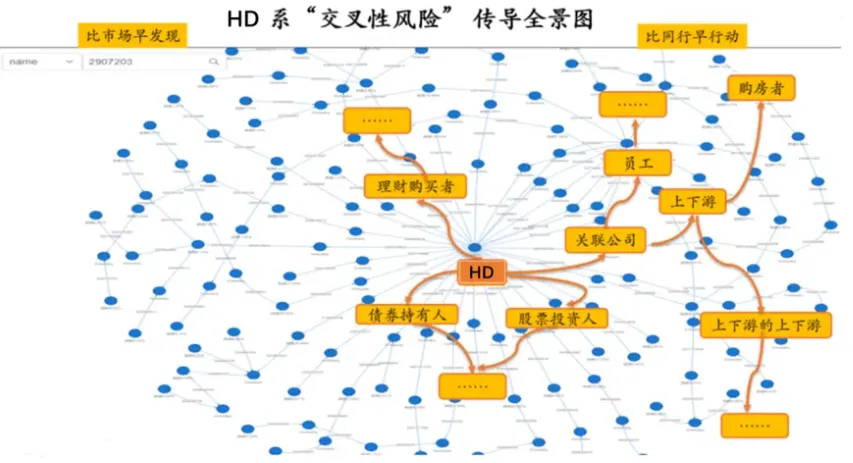
以HD为例，危机发生后，风险传播路径如下：

• 第一层：影响HD的关联公司；
• 第二层：影响公司员工和供应商；
• 第三层：影响购房者（供应商停止供货、工人停工，可能导致HD的在建工程停滞）。

风险从HD集团开始，逐步扩散至关联公司、员工、供应商、购房者等，形成了一张复杂的“网络”，呈现出明显的“链条效应”。

然而，许多与风险传导相关的实际应用并未采用图计算，而是依赖于手工计算，如银行KYC部门在计算UBO时仍使用Excel表。这种做法的效率和准确率可想而知。这与金融机构IT系统的陈旧和工作方法的落后有直接关系，阻碍了业务的开展，如企业影响力分析。

企业影响力分析不仅涉及持股关系、生产供求关系等传统问题，还应包括与企业相关的所有金融行为和事件，以及与这些行为事件直接或间接相关的事务。分析的视角不应仅限于企业实体，而应扩展至企业发布的产品、债券等。

如下图所示，分析的核心是企业的某个债券，其价格下跌可能直接影响其他债券的价格：

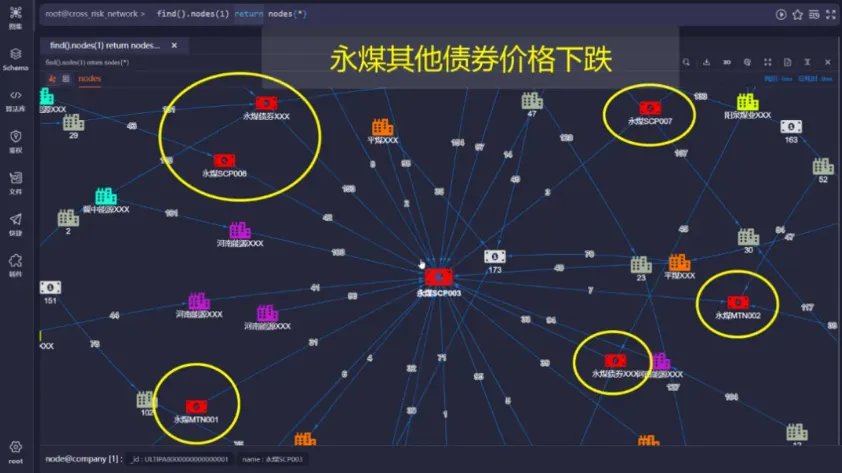
下图则标出了持有该债券的、可能受影响的省内其他企业：

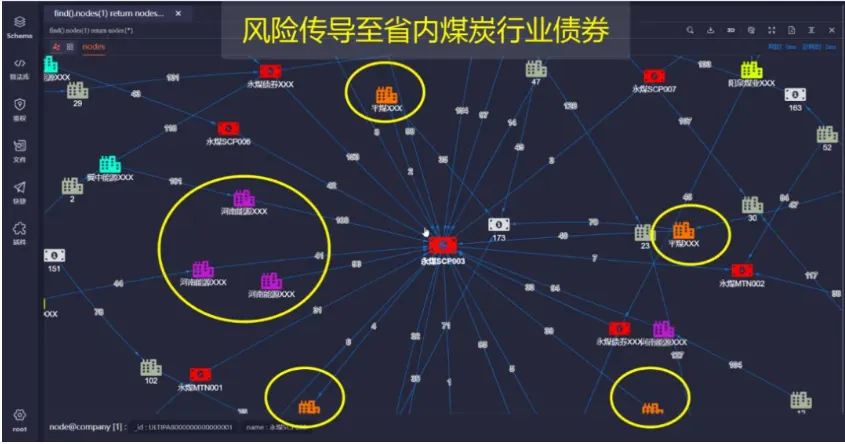
下图展示的是该债券的1步邻居，从这些邻居继续向外探寻就能得到该债券价格下跌后产生的危机传递效应：

专家们已越来越认识到，金融风险并不是孤立存在的，不同风险间具有链条效应，任何一只蝴蝶扇动翅膀，都有可能造成跨市场的风险传染——风险的关联性具有相互转化、传递和耦合的特点——图技术与蝴蝶效应在本质上是不谋而合的，即通过深度挖掘不同来源的数据，以网络化分析的方式去洞察。

此外，金融场景是一种基于长链条计算的场景，这就导致技术实现时的规则更为复杂，因为会涉及到各种回溯、归因，而且数据的计算量更大，同时也更注重时效性。只有实现真正的实时、全面、深度穿透、逐笔追溯、精准计量的监测和预警，才能保障金融风控中不会出现“蝴蝶效应”式的风险发生。

值得注意的是，图往往包含着复杂的属性及定义，例如：边的有向、无向，边的属性权重，K 邻是否包含 K-1 邻，如何处理计算环路等等，这些问题会导致 K 邻算法具体实现的差异。此外，在一些实际场景中，图自身拓扑结构的变化，过滤条件的设定，节点、边属性的变化都会影响到 K 邻计算的结果。

在行业应用中，K邻算法通常应用于多模态的异构图，即将多个单一信息的图融合在一起形成的综合性图谱。这对算法实现者的数据收集和构图能力提出了高要求，同时也对K邻算法的灵活性和功能性提出了更高标准。嬴图的高密度并发图算法库是目前全球运行最快、最丰富的图算法集合，支持通过EXTA接口进行热插拔和扩展。

如果在公开资料中看到K邻算法的应用多是同构图（只有一种点、一种边），可能是因为作者想通过简单的例子阐明观点，或者因为构图能力不足限制了算法的应用，也可能是K邻算法的实现不尽人意，无法对异构图进行恰当处理。K邻算法的应用应该是广泛且实际的，能够解决现实问题的，如果是因为后面两种情况而限制了算法的“大展宏图”，那么相关图厂商就应该反思一二并提高自身了！

最后，一个优秀的算法设计不仅应具备解决问题的能力，还应关注计算效率，即算力。我们列举了一些高性能图计算系统应具备的核心能力，以供企业在评估市场上各种图计算产品时作为参考：

• 高速图搜索能力：高QPS/TPS、低延时，实时动态剪枝能力；
• 对任何规模图的深度、实时搜索与遍历能力（10层以上）；
• 高密度、高并发图计算引擎：极高的吞吐率；
• 成熟稳定的图数据库、图计算与存储引擎、图中台等；
• 可扩展的计算能力：支持垂直与水平可扩展；
• 3D+2D高维可视化、高性能的知识图谱Web前端系统；
• 便捷、低成本的二次开发能力（图查询语言、API/SDK、工具箱等）。

---

🔥 参与方式

《图算法：行业应用与实践》免费包邮送出 3 本！

抽奖方式：随机抽取 3 位小伙伴免费送出！
参与方式1：关注博主、点赞、收藏、评论区评论 （随机有效留言即可）（切记要点赞+收藏，否则抽奖无效，每个人最多评论三次！）
参与方式2：关注博主公众号，私信然后参与抽奖
活动截止时间：2024-5-18 22:00
当当网购买链接：https://product.dangdang.com/29705431.html