AVL树、红黑树

news2025/1/16 9:16:22

数据结构、算法总述：数据结构/算法 C/C++-CSDN博客

AVL树

定义

  1. 空二叉树是一个 AVL 树
  2. 如果 T 是一棵 AVL 树，那么其左右子树也是 AVL 树，并且 \left | h(ls)-h(rs) \right |\leq 1，h 是其左右子树的高度
  3. 树高为 O\left ( log\ n \right )

平衡因子：右子树高度 - 左子树高度

创建节点

由于 AVL 树的相关操作需要获取节点高度，因此我们需要为节点类添加 height 变量：

/* AVL 树节点类 */
struct TreeNode {
    int val{};          // 节点值
    int height = 0;     // 节点高度
    TreeNode *left{};   // 左子节点
    TreeNode *right{};  // 右子节点
    TreeNode() = default;
    explicit TreeNode(int x) : val(x){}
};

 “节点高度”是指从该节点到它的最远叶节点的距离，即所经过的“边”的数量。需要特别注意的是，叶节点的高度为 0 ，而空节点的高度为 −1 。我们将创建两个工具函数，分别用于获取和更新节点的高度：

/* 获取节点高度 */
int height(TreeNode *node) {
    // 空节点高度为 -1 ，叶节点高度为 0
    return node == nullptr ? -1 : node->height;
}

/* 更新节点高度 */
void updateHeight(TreeNode *node) {
    // 节点高度等于最高子树高度 + 1
    node->height = max(height(node->left), height(node->right)) + 1;
}

节点的平衡因子（balance factor）定义为节点左子树的高度减去右子树的高度，同时规定空节点的平衡因子为 0 。我们同样将获取节点平衡因子的功能封装成函数，方便后续使用：

/* 获取平衡因子 */
int balanceFactor(TreeNode *node) {
    // 空节点平衡因子为 0
    if (node == nullptr)
        return 0;
    // 节点平衡因子 = 左子树高度 - 右子树高度
    return height(node->left) - height(node->right);
}

旋转 

我们将平衡因子绝对值 >1 的节点称为“失衡节点”。根据节点失衡情况的不同，旋转操作分为四种：右旋、左旋、先右旋后左旋、先左旋后右旋。

右旋

/* 右旋操作 */
TreeNode *rightRotate(TreeNode *node) {
    TreeNode *child = node->left;
    TreeNode *grandChild = child->right;
    // 以 child 为原点，将 node 向右旋转
    child->right = node;
    node->left = grandChild;
    // 更新节点高度
    updateHeight(node);
    updateHeight(child);
    // 返回旋转后子树的根节点
    return child;
}
左旋

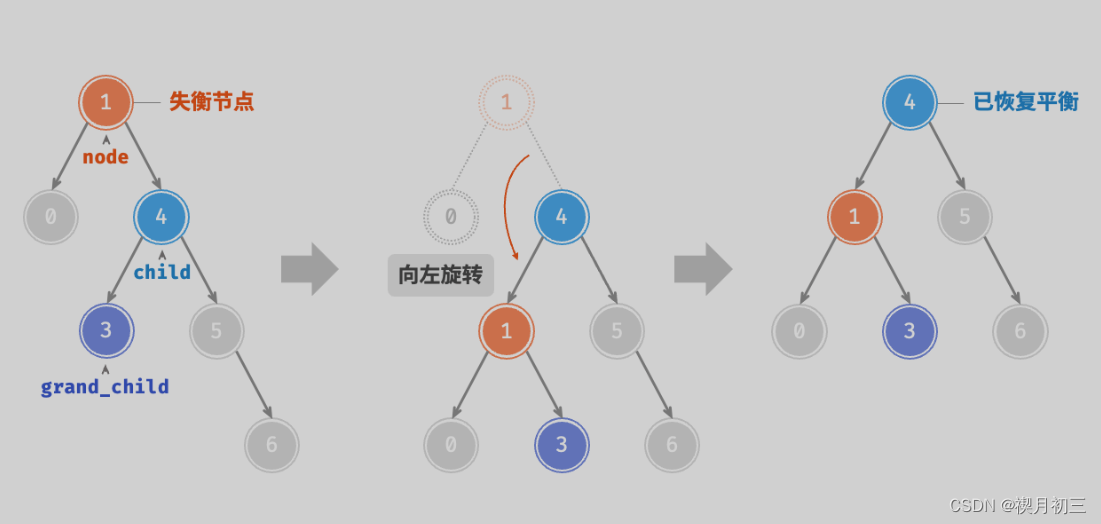
/* 左旋操作 */
TreeNode *leftRotate(TreeNode *node) {
    TreeNode *child = node->right;
    TreeNode *grandChild = child->left;
    // 以 child 为原点，将 node 向左旋转
    child->left = node;
    node->right = grandChild;
    // 更新节点高度
    updateHeight(node);
    updateHeight(child);
    // 返回旋转后子树的根节点
    return child;
}
先左旋后右旋

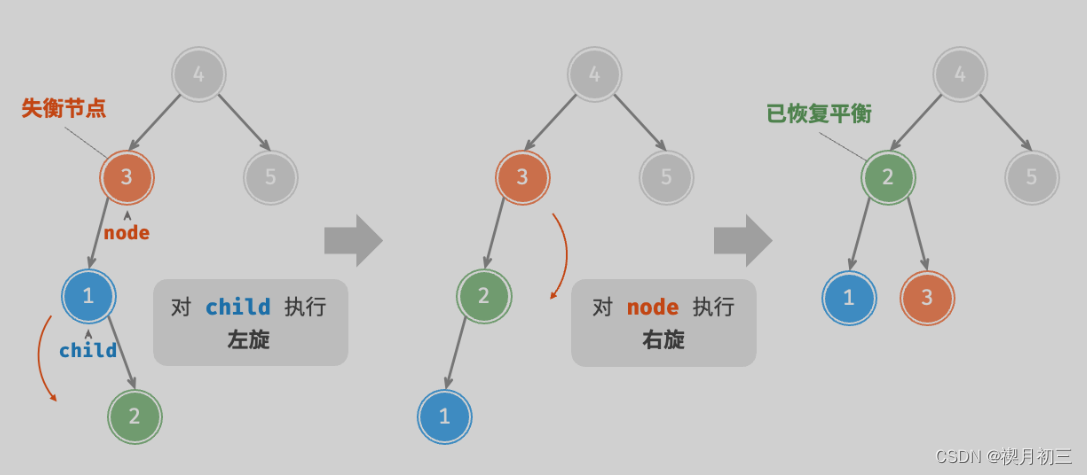
仅使用左旋或右旋都无法使子树恢复平衡。此时需要先对 child 执行“左旋”，再对 node 执行“右旋”。

先右旋后左旋

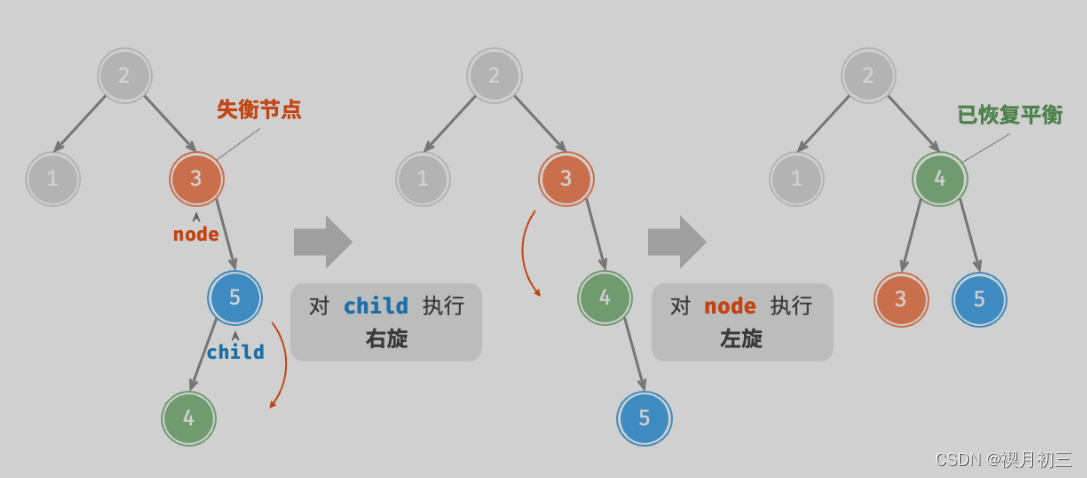
旋转的选择

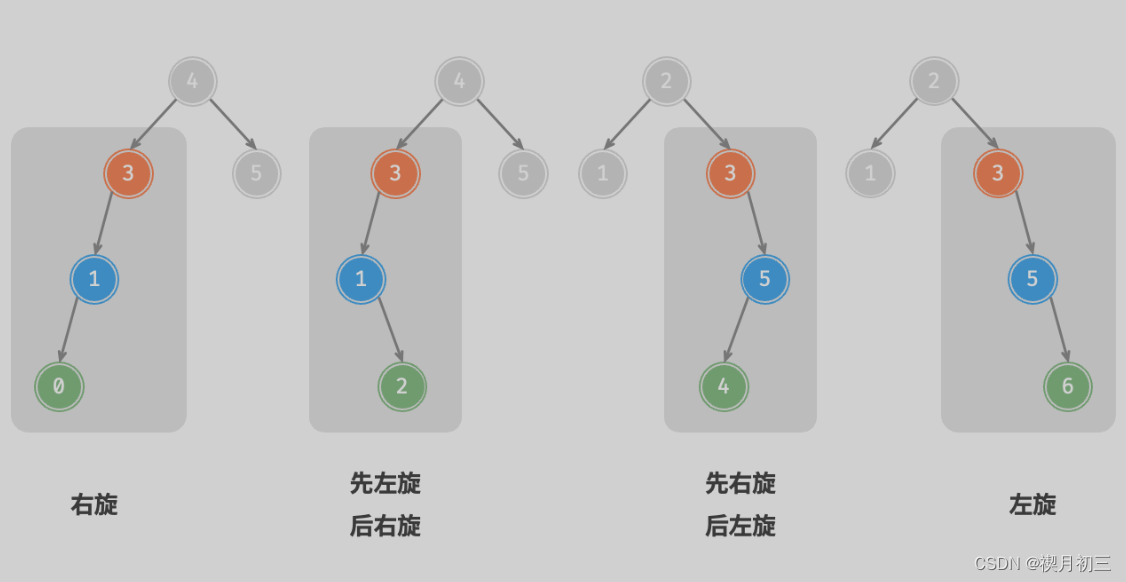
判断失衡节点的平衡因子以及较高一侧子节点的平衡因子的正负号，来确定旋转方式： 

失衡节点的平衡因子子节点的平衡因子旋转方式
>1≥0右旋
>1<0先左旋后右旋
<-1≤0左旋
<-1>0先右旋后左旋
/* 执行旋转操作，使该子树重新恢复平衡 */
TreeNode *rotate(TreeNode *node) {
    // 获取节点 node 的平衡因子
    int _balanceFactor = balanceFactor(node);
    // 左偏树
    if (_balanceFactor > 1) {
        if (balanceFactor(node->left) >= 0) {
            // 右旋
            return rightRotate(node);
        } else {
            // 先左旋后右旋
            node->left = leftRotate(node->left);
            return rightRotate(node);
        }
    }
    // 右偏树
    if (_balanceFactor < -1) {
        if (balanceFactor(node->right) <= 0) {
            // 左旋
            return leftRotate(node);
        } else {
            // 先右旋后左旋
            node->right = rightRotate(node->right);
            return leftRotate(node);
        }
    }
    // 平衡树，无须旋转，直接返回
    return node;
}

基础操作

插入

在 AVL 树中插入节点后，从该节点到根节点的路径上可能会出现一系列失衡节点。因此，我们需要从这个节点开始，自底向上执行旋转操作，使所有失衡节点恢复平衡。

/* 插入节点 */
void insert(int val) {
    root = insertHelper(root, val);
}

/* 递归插入节点（辅助方法） */
TreeNode *insertHelper(TreeNode *node, int val) {
    if (node == nullptr)
        return new TreeNode(val);
    /* 1. 查找插入位置并插入节点 */
    if (val < node->val)
        node->left = insertHelper(node->left, val);
    else if (val > node->val)
        node->right = insertHelper(node->right, val);
    else
        return node;    // 重复节点不插入，直接返回
    updateHeight(node); // 更新节点高度
    /* 2. 执行旋转操作，使该子树重新恢复平衡 */
    node = rotate(node);
    // 返回子树的根节点
    return node;
}
删除

在二叉搜索树的删除节点方法的基础上，需要从底至顶执行旋转操作，使所有失衡节点恢复平衡。

/* 删除节点 */
void remove(int val) {
    root = removeHelper(root, val);
}

/* 递归删除节点（辅助方法） */
TreeNode *removeHelper(TreeNode *node, int val) {
    if (node == nullptr)
        return nullptr;
    /* 1. 查找节点并删除 */
    if (val < node->val)
        node->left = removeHelper(node->left, val);
    else if (val > node->val)
        node->right = removeHelper(node->right, val);
    else {
        if (node->left == nullptr || node->right == nullptr) {
            TreeNode *child = node->left != nullptr ? node->left : node->right;
            // 子节点数量 = 0 ，直接删除 node 并返回
            if (child == nullptr) {
                delete node;
                return nullptr;
            }
            // 子节点数量 = 1 ，直接删除 node
            else {
                delete node;
                node = child;
            }
        } else {
            // 子节点数量 = 2 ，则将中序遍历的下个节点删除，并用该节点替换当前节点
            TreeNode *temp = node->right;
            while (temp->left != nullptr) {
                temp = temp->left;
            }
            int tempVal = temp->val;
            node->right = removeHelper(node->right, temp->val);
            node->val = tempVal;
        }
    }
    updateHeight(node); // 更新节点高度
    /* 2. 执行旋转操作，使该子树重新恢复平衡 */
    node = rotate(node);
    // 返回子树的根节点
    return node;
}
查找

与二叉搜索树一致

AVL树总代码

AVLTree.h

#include <iostream>
#include <assert.h>
using namespace std;

template<class K, class V>
struct AVLTreeNode
{
    AVLTreeNode* _left;
    AVLTreeNode* _right;
    AVLTreeNode* _parent;
    int _bf; // balance factor
    pair<K, V> _kv;

    AVLTreeNode(const pair<K, V>& kv)
        : _left(nullptr)
        , _right(nullptr)
        , _parent(nullptr)
        , _bf(0)
        , _kv(kv)
    {}
};

template<class K, class V>
class AVLTree
{
    typedef AVLTreeNode<K, V> Node;
public:
    bool Insert(const pair<K, V>& kv)
    {
        if (_root == nullptr)
        {
            _root = new Node(kv);
        }

        Node* cur = _root;
        Node* parent = nullptr;

        while (cur)
        {
            if (cur->_kv.first < kv.first)
            {
                parent = cur;
                cur = cur->_right;
            }
            else if (cur->_kv.first > kv.first)
            {
                parent = cur;
                cur = cur->_left;
            }
            else
            {
                return false;
            }
        }

        cur = new Node(kv);

        if (parent->_kv.first > kv.first)
            parent->_left = cur;
        else
            parent->_right = cur;

        cur->_parent = parent;

        while (parent)//最坏情况一直更新到root，此时parent为nullptr
        {
            if (cur == parent->_left)//更新平衡因子
                parent->_bf--;
            else
                parent->_bf++;

            if (parent->_bf == 0)
            {
                break;
            }
            else if (parent->_bf == 1 || parent->_bf == -1)//向上查找，检测是否出现不平衡
            {
                cur = cur->_parent;
                parent = parent->_parent;
            }
            else if (parent->_bf == 2 || parent->_bf == -2)
            {
                //旋转
                if (parent->_bf == 2 && cur->_bf == 1)//2，1说明右边子树深度阶梯式增加，所以往左旋转
                    RotateL(parent);//左单旋
                else if (parent->_bf == -2 && cur->_bf == -1)//-2，-1说明左边子树深度阶梯式增加，所以往右旋转
                    RotateR(parent);//右单旋
                else if (parent->_bf == -2 && cur->_bf == 1)//-2, 1说明左边子树中间深，先左单旋提高中间节点，再右单旋提高中间节点
                    RotateLR(parent);
                else if (parent->_bf == 2 && cur->_bf == -1)//2, -1说明右边子树中间深，先右单旋提高中间节点，再左单旋提高中间节点
                    RotateRL(parent);
                else
                    assert(false);

                break;
            }
            else //说明插入前AVL出现了问题，直接报错
            {
                assert(false);
            }
        }

        return true;
    }

    //左单旋
    void RotateL(Node* parent)
    {
        Node* subR = parent->_right;
        Node* subRL = subR->_left;

        parent->_right = subRL;
        if (subRL)
            subRL->_parent = parent;

        subR->_left = parent;
        Node* ppNode = parent->_parent;
        parent->_parent = subR;

        if (parent == _root)
        {
            _root = subR;
            subR->_parent = nullptr;
        }
        else
        {
            if (ppNode->_left == parent)
                ppNode->_left = subR;
            else
                ppNode->_right = subR;

            subR->_parent = ppNode;
        }

        parent->_bf = 0;
        subR->_bf = 0;
    }

    //右单旋
    void RotateR(Node* parent)
    {
        Node* subL = parent->_left;
        Node* subLR = subL->_right;

        parent->_left = subLR;
        if (subLR)
            subLR->_parent = parent;

        subL->_right = parent;
        Node* ppNode = parent->_parent;
        parent->_parent = subL;

        if (parent == _root)
        {
            _root = subL;
            subL->_parent = nullptr;
        }
        else
        {
            if (ppNode->_left == parent)
                ppNode->_left = subL;
            else
                ppNode->_right = subL;

            subL->_parent = ppNode;
        }

        parent->_bf = 0;
        subL->_bf = 0;
    }

    //左右双旋
    void RotateLR(Node* parent)
    {
        Node* subL = parent->_left;
        Node* subLR = subL->_right;

        int bf = subLR->_bf;
        RotateL(parent->_left);
        RotateR(parent);

        if (bf == -1)
        {
            subLR->_bf = 0;
            subL->_bf = 0;
            parent->_bf = 1;
        }
        else if (bf == 1)
        {
            subLR->_bf = 0;
            subL->_bf = -1;
            parent->_bf = 0;
        }
        else if (bf == 0)
        {
            subLR->_bf = 0;
            subL->_bf = 0;
            parent->_bf = 0;
        }
        else
        {
            assert(false);
        }
    }

    //右左双旋
    void RotateRL(Node* parent)
    {
        Node* subR = parent->_right;
        Node* subRL = subR->_left;

        int bf = subRL->_bf;
        RotateR(parent->_right);
        RotateL(parent);

        if (bf == -1)
        {
            subR->_bf = 1;
            subRL->_bf = 0;
            parent->_bf = 0;
        }
        else if (bf == 1)
        {
            subR->_bf = 0;
            subRL->_bf = 0;
            parent->_bf = -1;
        }
        else if (bf == 0)
        {
            subR->_bf = 0;
            subRL->_bf = 0;
            parent->_bf = 0;
        }
        else
        {
            assert(false);
        }
    }
    
    //中序
    void InOrder()
    {
        _InOrder(_root);
        cout << "end" << endl;
    }
    
private:
    //中序
    void _InOrder(Node* root)
    {
        if (root == nullptr)
            return;

        _InOrder(root->_left);
        cout << root->_kv.first << " - ";

        _InOrder(root->_right);
    }
    
    Node* _root = nullptr;
};

应用

  • 组织和存储大型数据，适用于高频查找、低频增删的场景。 

红黑树

红黑树是一种自平衡的二叉搜索树。每个节点额外存储了一个 color 字段 ("RED" or "BLACK")，用于确保树在插入和删除时保持平衡

性质

  1. 节点为红色或黑色
  2. 根节点必须为黑色
  3. NIL 节点（空叶子节点）为黑色
  4. 红色节点的子节点为黑色
  5. 从根节点到 NIL 节点的每条路径上的黑色节点数量相同

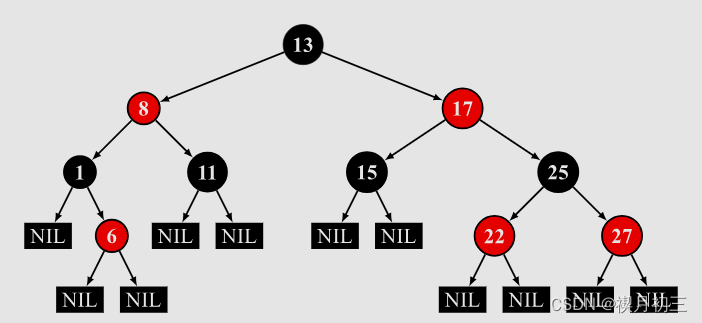
创建节点

enum Colour
{
    RED,
    BLACK
};

template<class K, class V>
struct RBTreeNode
{
    RBTreeNode* _left;
    RBTreeNode* _right;
    RBTreeNode* _parent;
    pair<K, V> _kv;
    Colour _col;
};

_left：左子树
_right：右子树
_parent：父节点
_kv：节点存储的值
_col：该节点的颜色

构造函数

RBTreeNode(const pair<K, V>& kv)
    : _left(nullptr)
    , _right(nullptr)
    , _parent(nullptr)
    , _kv(kv)
    , _col(RED)//初始化为红节点
{}

红黑树本体，类中只存储根节点_root

template<class K, class V>
class RBTree
{
    typedef RBTreeNode<K, V> Node;
private:
	Node* _root = nullptr;
}

插入

以二叉搜索树插入逻辑为基础：

bool Insert(const pair<K, V>& kv)
{
    if (_root == nullptr)
    {
        _root = new Node(kv);
        _root->_col = BLACK;//保持根为黑节点
    }

    Node* cur = _root;
    Node* parent = nullptr;

    while (cur)
    {
        if (cur->_kv.first < kv.first)
        {
            parent = cur;
            cur = cur->_right;
        }
        else if (cur->_kv.first > kv.first)
        {
            parent = cur;
            cur = cur->_left;
        }
        else
        {
            return false;
        }
    }

    cur = new Node(kv);

    if (parent->_kv.first > kv.first)
        parent->_left = cur;
    else
        parent->_right = cur;

    cur->_parent = parent;
   
   //调整红黑树
   //......
   //......
   //......
   
    return true;
}

代码分析：

if (_root == nullptr)
{
	_root = new Node(kv);
    _root->_col = BLACK;//保持根为黑节点
}

插入节点时，根节点_root为空，说明当前整棵树都为空，那么直接插入值作为根节点即可，但是根节点必须是黑色节点，而我们新插入的节点是红色，所以要将其调整为黑色节点。

while (cur)
{
	if (cur->_kv.first < kv.first)
	{
		parent = cur;
		cur = cur->_right;
	}
	else if (cur->_kv.first > kv.first)
	{
		parent = cur;
		cur = cur->_left;
	}
	else
	{
		return false;
	}
}

找到合适的插入位置，当key大于当前节点cur->_kv.first < kv.first，那么cur就向左寻找，反之向右寻找。如果当前节点值等于key，那么说明该节点已经存在，返回false代表插入失败。当我们的cur为空指针，说明已经找到了插入的节点，此时跳出循环进行插入。

cur = new Node(kv);

if (parent->_kv.first > kv.first)
	parent->_left = cur;
else
	parent->_right = cur;

cur->_parent = parent;

到达此处，说明前面已经找到插入的位置了，而parent节点就是插入位置的父亲节点。根据key的大小，来判断插入到左边还是右边，插入完成后，再让新节点的_parent指向parent。

分情况调整红黑树

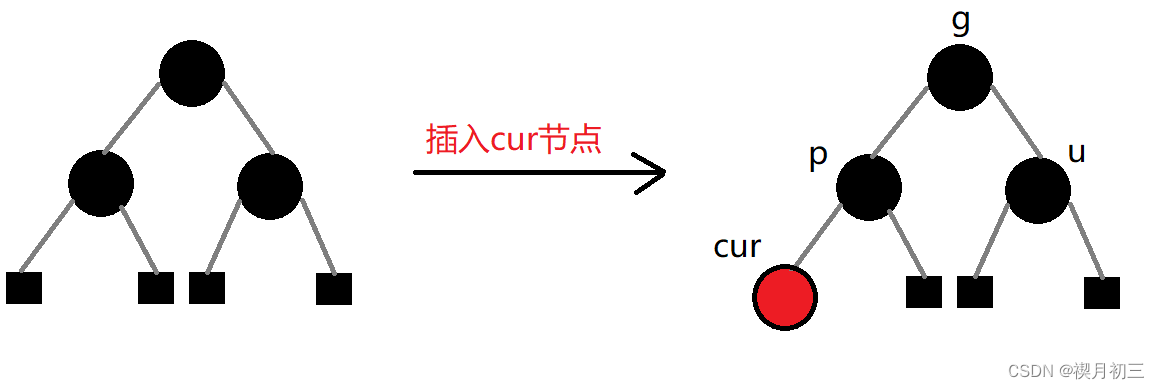
对于红黑树的插入，我们需要关注新节点的父亲parent，祖父grandfather，叔叔uncle三个节点：

1.根据parent节点的颜色，来判断是否需要调整
parent节点为黑色

新插入的节点默认为红色，所以新插入节点不会影响路径上黑色节点的数目，而parent是黑节点，我们也没有出现连续的红色节点，所以这种情况无需任何调整，直接插入就可以。

parent节点为红色

 如果父亲节点为红色，我们就会出现连续的红色节点，这时我们就需要进行调整了

当parent为红色，我们就需要再根据uncle的颜色，将插入分类两类：uncle为红色以及uncle为黑色 

注意：由于parent是红色节点，此时的grandfather一定是黑色节点

2.根据uncle节点的颜色，来判断如何调整
uncle节点为红色

当uncle节点为红色，此时需要进行变色

由于新插入了红色的cur节点，此时parent与cur出现了连续的红色节点，于是我们将parent改为黑色。但是此时以parent为根的所有路径就会多出一个黑节点，于是把grandfather变为红色，来抵消这个新增的黑节点。但是此时以uncle为根的路径又会少一个黑节点，于是把uncle变黑

但是我们将grandfather变为了红色，这有可能会影响到上一层节点

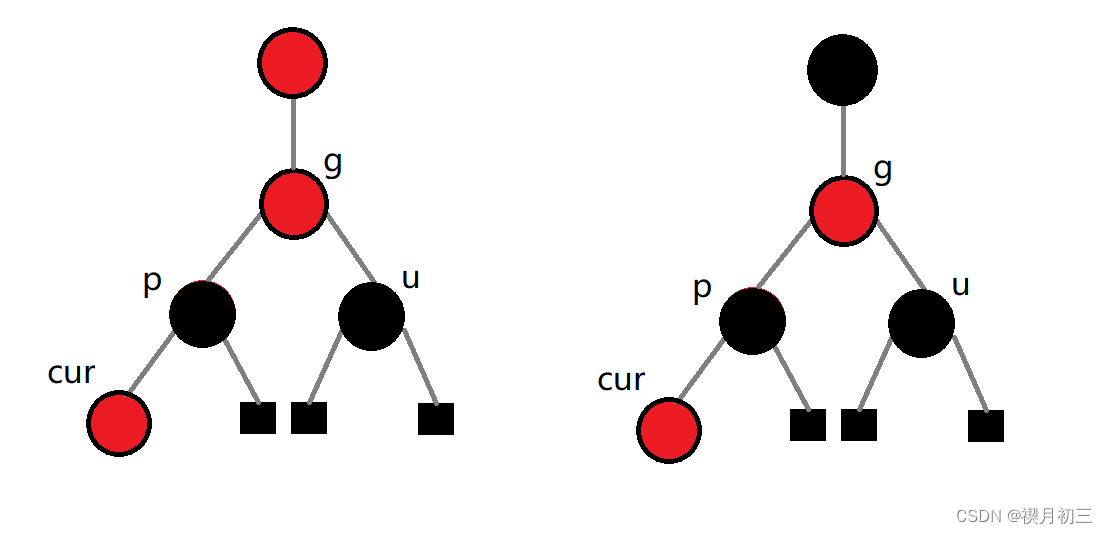
grandfather变红之后，可能出现两个红色节点相连的情况，所以我们要写一个while循环，来反复向上检查。

while (parent && parent->_col == RED)//只有parent为红，才更新 (parent可能不存在)
{
    Node* grandfather = parent->_parent;
    if (parent == grandfather->_left)
    {
        Node* uncle = grandfather->_right;

        //uncle存在且为红节点
        if (uncle && uncle->_col == RED)
        {
            parent->_col = uncle->_col = BLACK;
            grandfather->_col = RED;

            cur = grandfather;
            parent = cur->_parent;
        }
        else//uncle为黑节点 
        {
            //其它处理
        }
    }
    else
    {
        Node* uncle = grandfather->_left;

        //uncle存在且为红节点
        if (uncle && uncle->_col == RED)
        {
            parent->_col = uncle->_col = BLACK;
            grandfather->_col = RED;

            cur = grandfather;
            parent = cur->_parent;
        }
        else//uncle为黑节点 
        {
        	//其它处理
        }
    }
}

_root->_col = BLACK;//在循环内部不判断root情况，统一处理

代码分析：

while (parent && parent->_col == RED)

用于检测cur的parent的颜色，通过我们前面的推导，如果parent为红色才需要调整，因此进入循环的条件之一是parent为红色。另外的parent有可能为NIL，此时我们要避免访问空指针，所以空指针也不能进循环

if (parent == grandfather->_left)
{  }
else
{ }

检测parent 节点是grandfather的左子树还是右子树，这将涉及到如何找uncle以及下一种情况的调整，此时我们要分类讨论：
当parent == grandfather->_left成立，那么uncle就是grandfather的右子树：Node* uncle = grandfather->_right;，反之就是左子树

if (uncle && uncle->_col == RED)
{
	parent->_col = uncle->_col = BLACK;
	grandfather->_col = RED;

	cur = grandfather;
	parent = cur->_parent;
}

找到uncle后，如果uncle是红色，那么直接进行变色操作，把parent和uncle的颜色变为黑色，grandfather变为红色。
随后由于我们的变色操作可能会影响上一层，此时调整节点，进入下一次while循环

_root->_col = BLACK;

在先前的while循环中，有可能出现对_root节点的操作，导致_root的颜色改变，而_root需要保持黑色。如果我们在循环内部，每一次都检测_root有点麻烦了，于是我们直接在每一次调整完节点后，把_root强行矫正为黑色

uncle节点为黑色

又因为红黑树中，NIL也算作黑色节点，所以uncle为黑色分为以下两种情况：

  1. uncle为空指针
  2. uncle不为空指针

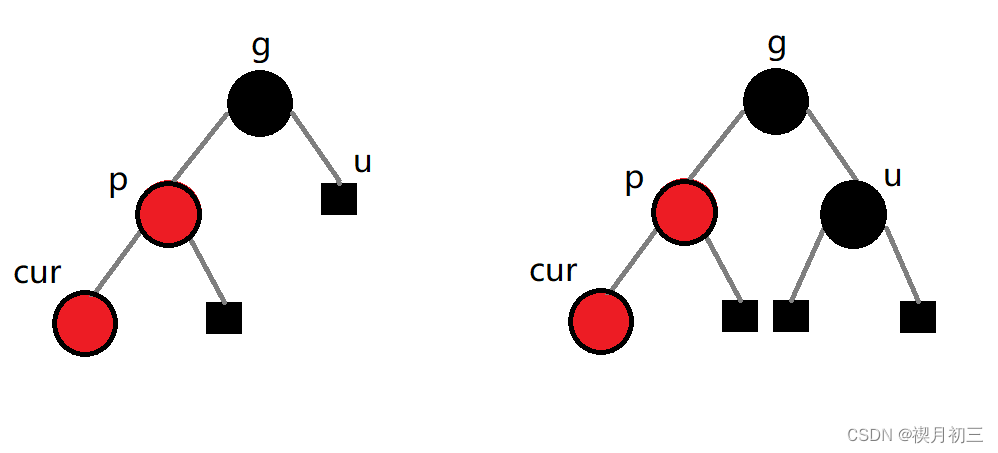
 如果 uncle为空指针，那么cur一定是新插入的节点。

因为如果cur不是新插入的节点，那么cur和parent一定有一个原先是黑色节点，不然会出现连续的红色节点。但是如果cur和parent有一个是黑色节点，那么grandfather的左子树就比右子树多出一个黑节点，这就违背了红黑树规则。无论怎样，原先的树都不可能符合规则，所以cur一定是新插入的节点，破坏了规则。

如果 uncle不为空指针，那么cur一定是从黑色节点变成的红色节点（不是新插入的）。

因为如果uncle存在，那么grandfather的右子树就存在一个黑节点，而parent是红节点，所以cur和parent的右子树中都至少有一个黑节点，才能保证每一条路径黑节点数目相同。因此cur原先一定是黑节点，是因为cur下层插入了新节点，然后通过while循环向上走，影响到了当前层。

对于这种uncle为黑色的情况，我们需要通过旋转+变色来维持红黑树。

旋转又分单旋和双旋（同AVL树）

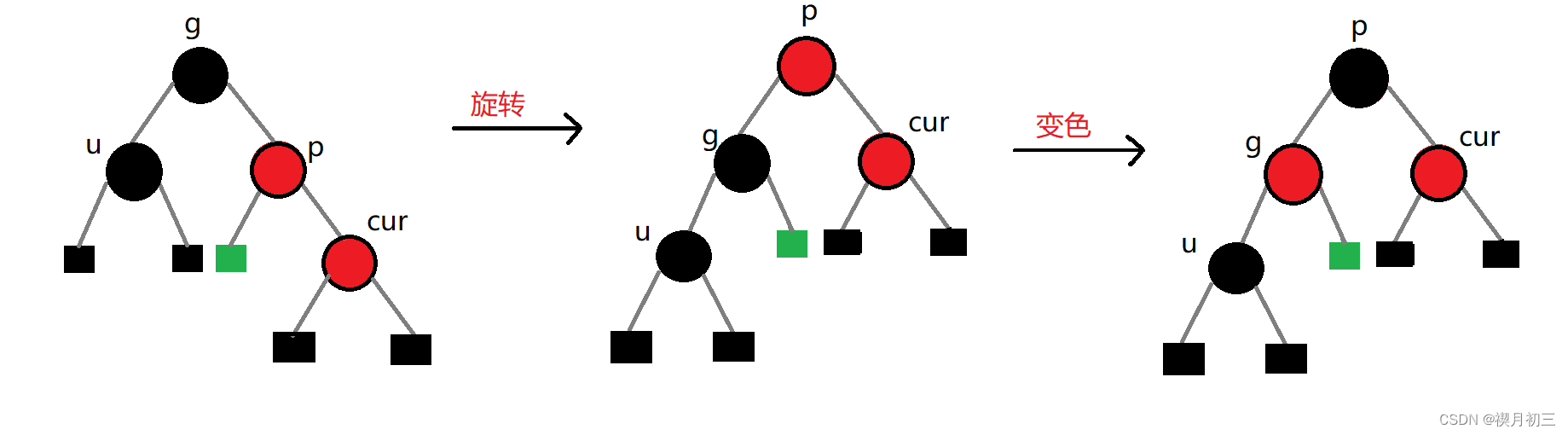
当cur与parent的关系和parent与grandfather的关系一致时，需要进行单旋

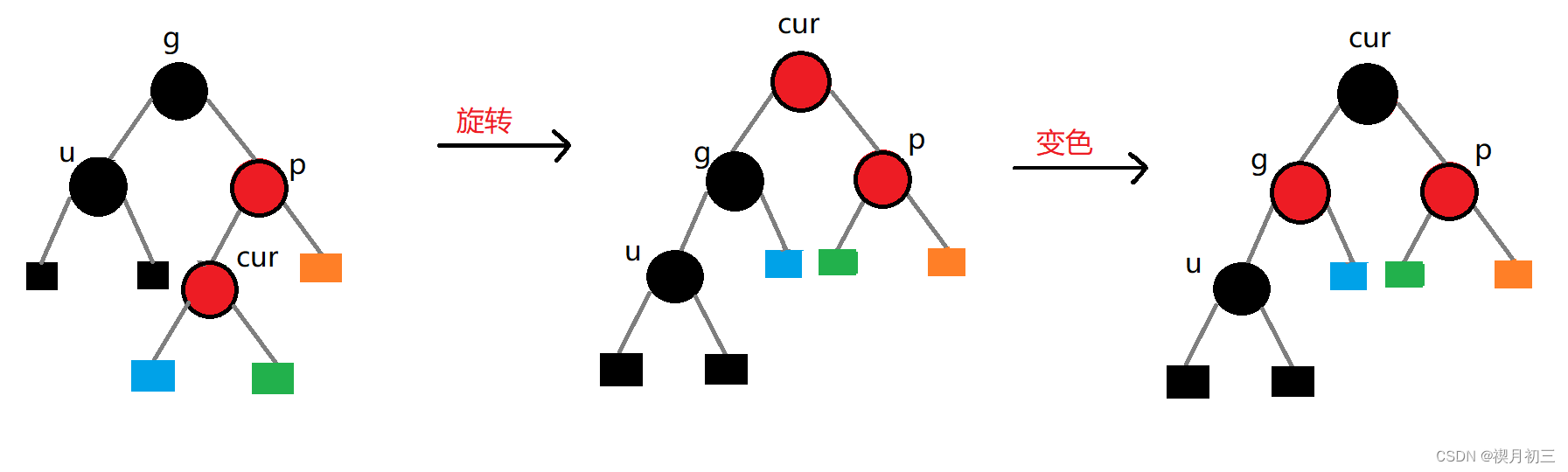
当cur与parent的关系和parent与grandfather的关系不一致时，需要进行双旋 

 

当parent == grandfather->_left

else//uncle为黑节点 (旋转)
{
    if (cur == parent->_left)
    {
        RotateR(grandfather);//右单旋
        parent->_col = BLACK;//变色
        grandfather->_col = RED;//变色
    }
    else
    {
        RotateL(parent);//左右双旋 - 左单旋
        RotateR(grandfather);//左右双旋 - 右单旋

        cur->_col = BLACK;//变色
        grandfather->_col = RED;//变色
    }

    break;//旋转后一定平衡
}

当parent == grandfather->_right

else//uncle为黑节点 (旋转)
{
    if (cur == parent->_right)
    {
        RotateL(grandfather);//左单旋
        parent->_col = BLACK;//变色
        grandfather->_col = RED;//变色
    }
    else
    {
        RotateR(parent);//右左双旋 - 右单旋
        RotateL(grandfather);//右左双旋 - 左单旋

        cur->_col = BLACK;//变色
        grandfather->_col = RED;//变色
    }

    break;//旋转后一定平衡
}

insert总代码

bool Insert(const pair<K, V>& kv)
{
    if (_root == nullptr)
    {
        _root = new Node(kv);
        _root->_col = BLACK;//保持根为黑节点
    }

    Node* cur = _root;
    Node* parent = nullptr;

    while (cur)
    {
        if (cur->_kv.first < kv.first)
        {
            parent = cur;
            cur = cur->_right;
        }
        else if (cur->_kv.first > kv.first)
        {
            parent = cur;
            cur = cur->_left;
        }
        else
        {
            return false;
        }
    }

    cur = new Node(kv);

    if (parent->_kv.first > kv.first)
        parent->_left = cur;
    else
        parent->_right = cur;

    cur->_parent = parent;

    while (parent && parent->_col == RED)//只有parent为红，才更新 (parent可能不存在)
    {
        Node* grandfather = parent->_parent;
        if (parent == grandfather->_left)
        {
            Node* uncle = grandfather->_right;

            //uncle存在且为红节点
            if (uncle && uncle->_col == RED)
            {
                parent->_col = uncle->_col = BLACK;
                grandfather->_col = RED;

                cur = grandfather;
                parent = cur->_parent;
            }
            else//uncle不存在或为黑节点 (旋转)
            {
                if (cur == parent->_left)
                {
                    RotateR(grandfather);
                    parent->_col = BLACK;
                    grandfather->_col = RED;
                }
                else
                {
                    RotateL(parent);
                    RotateR(grandfather);


                    cur->_col = BLACK;
                    grandfather->_col = RED;
                }

                break;//旋转后一定平衡
            }
        }
        else
        {
            Node* uncle = grandfather->_left;

            //uncle存在且为红节点
            if (uncle && uncle->_col == RED)
            {
                parent->_col = uncle->_col = BLACK;
                grandfather->_col = RED;

                cur = grandfather;
                parent = cur->_parent;
            }
            else//uncle不存在或为黑节点 (旋转)
            {
                if (cur == parent->_right)
                {
                    RotateL(grandfather);
                    parent->_col = BLACK;
                    grandfather->_col = RED;
                }
                else
                {
                    RotateR(parent);
                    RotateL(grandfather);

                    cur->_col = BLACK;
                    grandfather->_col = RED;
                }

                break;//旋转后一定平衡
            }
        }
    }

    _root->_col = BLACK;//在循环内部不判断root情况，统一处理

    return true;
}

红黑树总代码

RBTree.h

#include <iostream>
#include <assert.h>
using namespace std;

enum Colour
{
    RED,
    BLACK
};

template<class K, class V>
struct RBTreeNode
{
    RBTreeNode* _left;
    RBTreeNode* _right;
    RBTreeNode* _parent;
    pair<K, V> _kv;
    Colour _col;

    RBTreeNode(const pair<K, V>& kv)
        : _left(nullptr)
        , _right(nullptr)
        , _parent(nullptr)
        , _kv(kv)
        , _col(RED)
    {}
};

template<class K, class V>
class RBTree
{
    typedef RBTreeNode<K, V> Node;
public:
    bool Insert(const pair<K, V>& kv)
    {
        if (_root == nullptr)
        {
            _root = new Node(kv);
            _root->_col = BLACK;//保持根为黑节点
        }

        Node* cur = _root;
        Node* parent = nullptr;

        while (cur)
        {
            if (cur->_kv.first < kv.first)
            {
                parent = cur;
                cur = cur->_right;
            }
            else if (cur->_kv.first > kv.first)
            {
                parent = cur;
                cur = cur->_left;
            }
            else
            {
                return false;
            }
        }

        cur = new Node(kv);

        if (parent->_kv.first > kv.first)
            parent->_left = cur;
        else
            parent->_right = cur;

        cur->_parent = parent;

        while (parent && parent->_col == RED)//只有parent为红，才更新 (parent可能不存在)
        {
            Node* grandfather = parent->_parent;
            if (parent == grandfather->_left)
            {
                Node* uncle = grandfather->_right;

                //uncle存在且为红节点
                if (uncle && uncle->_col == RED)
                {
                    parent->_col = uncle->_col = BLACK;
                    grandfather->_col = RED;

                    cur = grandfather;
                    parent = cur->_parent;
                }
                else//uncle不存在或为黑节点 (旋转)
                {
                    if (cur == parent->_left)
                    {
                        RotateR(grandfather);
                        parent->_col = BLACK;
                        grandfather->_col = RED;
                    }
                    else
                    {
                        RotateL(parent);
                        RotateR(grandfather);

                        cur->_col = BLACK;
                        grandfather->_col = RED;
                    }

                    break;//旋转后一定平衡
                }
            }
            else
            {
                Node* uncle = grandfather->_left;

                //uncle存在且为红节点
                if (uncle && uncle->_col == RED)
                {
                    parent->_col = uncle->_col = BLACK;
                    grandfather->_col = RED;

                    cur = grandfather;
                    parent = cur->_parent;
                }
                else//uncle不存在或为黑节点 (旋转)
                {
                    if (cur == parent->_right)
                    {
                        RotateL(grandfather);
                        parent->_col = BLACK;
                        grandfather->_col = RED;
                    }
                    else
                    {
                        RotateR(parent);
                        RotateL(grandfather);

                        cur->_col = BLACK;
                        grandfather->_col = RED;
                    }

                    break;//旋转后一定平衡
                }
            }
        }

        _root->_col = BLACK;//在循环内部不判断root情况，统一处理

        return true;
    }
    
    //左单旋
    void RotateL(Node* parent)
    {
        Node* subR = parent->_right;
        Node* subRL = subR->_left;

        parent->_right = subRL;
        if (subRL)
            subRL->_parent = parent;

        subR->_left = parent;
        Node* ppNode = parent->_parent;
        parent->_parent = subR;

        if (parent == _root)
        {
            _root = subR;
            subR->_parent = nullptr;
        }
        else
        {
            if (ppNode->_left == parent)
                ppNode->_left = subR;
            else
                ppNode->_right = subR;

            subR->_parent = ppNode;
        }
    }

    //右单旋
    void RotateR(Node* parent)
    {
        Node* subL = parent->_left;
        Node* subLR = subL->_right;

        parent->_left = subLR;
        if (subLR)
            subLR->_parent = parent;

        subL->_right = parent;
        Node* ppNode = parent->_parent;
        parent->_parent = subL;

        if (parent == _root)
        {
            _root = subL;
            subL->_parent = nullptr;
        }
        else
        {
            if (ppNode->_left == parent)
                ppNode->_left = subL;
            else
                ppNode->_right = subL;

            subL->_parent = ppNode;
        }
    }

    size_t Size()
    {
        return _Size(_root);
    }

    size_t _Size(Node* root)
    {
        if (root == nullptr)
            return 0;;

        return _Size(root->_left) + _Size(root->_right) + 1;
    }

    Node* Find(const K& key)
    {
        Node* cur = _root;

        while (cur)
        {
            if (cur->_kv.first < key)
            {
                cur = cur->_right;
            }
            else if (cur->_kv.first > key)
            {
                cur = cur->_left;
            }
            else
            {
                return cur;
            }
        }

        return nullptr;
    }

    //中序
    void InOrder()
    {
        _InOrder(_root);
        cout << "end" << endl;
    }

    int Height()
    {
        return _Height(_root);
    }

private:
    //中序
    void _InOrder(Node* root)
    {
        if (root == nullptr)
            return;

        _InOrder(root->_left);
        cout << root->_kv.first << " - ";

        _InOrder(root->_right);
    }

    //求高度
    int _Height(Node* root)
    {
        if (root == nullptr)
            return 0;

        return max(Height(root->_left), Height(root->_right)) + 1;
    }

    Node* _root = nullptr;
};

应用

  • 作为map&set的底层

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1674936.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

棒材直线度测量仪 专为圆形产品研发设计 在线无损检测

棒材直线度测量仪 专为圆形产品研发设计 在线无损检测

棒材直线度测量仪采用了先进的技术&#xff0c;能够实现在线无损检测&#xff0c;为生产过程提供了极大的便利。专为圆形产品设计&#xff0c;它能够精确测量棒材的米直线度及外径、椭圆度尺寸&#xff0c;为质量控制提供可靠的数据支持。 在线直线度测量仪不仅具有出色的性能…
阅读更多...
C++实战演练---负载均衡在线oj项目 || 编译服务模块设计

C++实战演练---负载均衡在线oj项目 || 编译服务模块设计

顾得泉&#xff1a;个人主页 个人专栏&#xff1a;《Linux操作系统》 《C从入门到精通》 《LeedCode刷题》 键盘敲烂&#xff0c;年薪百万&#xff01; 前言 上一篇预热文章简单说过我们的编写思路&#xff0c;首先要实现的是编译功能&#xff0c;那么在编译功能版块中&…
阅读更多...
好消息|NIH给博士后加薪，起步年薪6.1万美元

好消息|NIH给博士后加薪，起步年薪6.1万美元

近日美国国立卫生研究院&#xff08;NIH&#xff09;正式宣布提高其资助的博士后年薪为61,008美元并根据经验资历进一步向上调整。同时NIH承诺未来3-5年内将博士后的最低年薪提高到70000美元。对于有望从事博士后研究的科研人员而言&#xff0c;这是一个好消息&#xff0c;为此…
阅读更多...
水面垃圾监测识别摄像机

水面垃圾监测识别摄像机

随着城市化进程的加快和旅游业的兴起&#xff0c;水域环境污染问题日益突出&#xff0c;水面垃圾成为环境保护的重要问题。为有效监测和清理水面垃圾&#xff0c;水面垃圾监测识别摄像机应运而生。水面垃圾监测识别摄像机利用高清晰度摄像头和智能识别算法&#xff0c;能够实时…
阅读更多...
springcloud简单了解及上手

springcloud简单了解及上手

springcloud微服务框架简单上手 文章目录 springcloud微服务框架简单上手一、SpringCloud简单介绍1.1 单体架构1.2 分布式架构1.3 微服务 二、SpringCloud与SpringBoot的版本对应关系2022.x 分支2021.x 分支2.2.x 分支 三、Nacos注册中心3.1 认识和安装Nacos3.2 配置Nacos3.3 n…
阅读更多...
BM11 链表相加(二)

BM11 链表相加(二)

描述 假设链表中每一个节点的值都在 0 - 9 之间&#xff0c;那么链表整体就可以代表一个整数。 给定两个这种链表&#xff0c;请生成代表两个整数相加值的结果链表。 数据范围&#xff1a;0≤&#x1d45b;,&#x1d45a;≤10000000≤n,m≤1000000&#xff0c;链表任意值 0≤…
阅读更多...
centos7.9安装PHP运行环境

centos7.9安装PHP运行环境

MySQL安装 报错&#xff1a;源 "MySQL 8.0 Community Server" 的 GPG 密钥已安装&#xff0c;但是不适用于此软件包。请检查源的公钥 URL 是否配置正确。 解决&#xff1a; yum install mysql-server -y --nogpgcheck 查询初始密码 grep temporary password /var…
阅读更多...
SpringBoot实现 QQ邮箱验证码

SpringBoot实现 QQ邮箱验证码

SpringBoot实现 QQ邮箱验证码 文章目录 SpringBoot实现 QQ邮箱验证码一、开通SMTP校验码1.登录qq邮箱2.开启SMTP服务3.发送手机短信4.得到授权码 二、回到spring项目中1.导入所需依赖2.验证码工具类3.具体实现逻辑(serviceimpl) 三、测试qq邮箱验证码 一、开通SMTP校验码 1.登…
阅读更多...
基于Java+SpringBoot+vue+elementui 实现猜灯谜答题抽奖系统

基于Java+SpringBoot+vue+elementui 实现猜灯谜答题抽奖系统

目录 系统简介效果图1、手机答题端2、后台系统管理 源码结构源码下载地址技术交流 博主介绍&#xff1a; 计算机科班人&#xff0c;全栈工程师&#xff0c;掌握C、C#、Java、Python、Android等主流编程语言&#xff0c;同时也熟练掌握mysql、oracle、sqlserver等主流数据库&…
阅读更多...
Linux环境变量详解

Linux环境变量详解

文章目录 1. 前言2 什么是PATH环境变量3. 如何添加PATH环境变量4. 系统中的其他环境变量5. 环境变量的由来6. 环境变量的基本操作6.1 设置环境变量6.2 通过getenv获取环境变量6.3 环境变量的应用场景 7. 通过命令行参数获取环境变量 1. 前言 本篇文章将以PATH环境变量为例来对整…
阅读更多...
CSP备考---位运算

CSP备考---位运算

前言 本期我们将学习位运算&#xff0c;与本期类型的考点&#xff08;二进制转换&#xff09;反码、补码、原码。 1、位运算是什么 首先我们需要先了解位运算是什么。 我们知道&#xff0c;计算机中的数在内存中都是以二进制形式进行存储的 &#xff0c;而位运算就是直接对整…
阅读更多...
J-STAGE (日本电子科学与技术信息集成)数据库介绍及文献下载

J-STAGE (日本电子科学与技术信息集成)数据库介绍及文献下载

J-STAGE (日本电子科学与技术信息集成)是日本学术出版物的平台。它由日本科学技术振兴机构&#xff08;JST&#xff09;开发和管理。该系统不仅包括期刊&#xff0c;还有论文集&#xff0c;研究报告、技术报告等。文献多为英文&#xff0c;少数为日文。目前网站上所发布的内容来…
阅读更多...
通过windows远程桌面，远程连接CentOS系统

通过windows远程桌面，远程连接CentOS系统

1.配置阿里云的YUM仓库 1.1 备份当前的YUM仓库配置文件 sudo cp /etc/yum.repos.d/CentOS-Base.repo /etc/yum.repos.d/CentOS-Base.repo.backup1.2 下载阿里云的CentOS仓库配置文件 对于CentOS 7&#xff1a; sudo wget -O /etc/yum.repos.d/CentOS-Base.repo http://mirr…
阅读更多...
Java RMI反序列化总结篇-01

Java RMI反序列化总结篇-01

1.java rmi反序列化 RMI 允许一个应用程序访问另外一个服务器或虚拟机上的对象&#xff0c;方法和服务&#xff0c;它使远程方法调用就像在本地调用一样简单。它为用户屏蔽了底层的网络传输细节&#xff0c;使用的时候只需适当处理异常即可。所以 RMI 是非常容易使用的&#x…
阅读更多...
uniapp开发安卓app使用文字转语音技术

uniapp开发安卓app使用文字转语音技术

在 UniApp 开发安卓应用时&#xff0c;要实现文字转语音&#xff08;Text-to-Speech, TTS&#xff09;技术&#xff0c;你可以利用 UniApp 的跨平台能力结合原生模块或第三方服务来实现。以下是一些建议的步骤和方法&#xff1a; 1. 使用 UniApp 原生模块&#xff08;如果支持…
阅读更多...
Linux中的磁盘分析工具ncdu

Linux中的磁盘分析工具ncdu

2024年5月14日&#xff0c;周二上午 概述 ncdu 是一个基于文本的用户界面磁盘使用情况分析工具。它可以在终端中快速扫描目录&#xff0c;并统计该目录下的文件和文件夹的磁盘使用情况&#xff0c;以交互友好的方式呈现给用户。 安装 在 Debian/Ubuntu 系统下&#xff0c;可…
阅读更多...
Linux的命名管道 共享内存 信号量

Linux的命名管道 共享内存 信号量

目录 命名管道 mkfifo函数 unlink函数 命名管道类 服务端 客户端 共享内存 shmget函数 ftok函数 key和shmid的区别 snprintf函数 ipcs指令 ipcrm指令 shmctl函数 shmat函数 void*做返回值 创建共享内存空间 服务端 客户端 信号量 命名管道 基本概念&a…
阅读更多...
Unity使用sherpa-onnx实现离线语音合成

Unity使用sherpa-onnx实现离线语音合成

sherpa-onnx https://github.com/k2-fsa/sherpa-onnx 相关dll和lib库拷进Unity&#xff0c;官方示例代码稍作修改 using SherpaOnnx; using System; using System.IO; using System.Runtime.InteropServices; using UnityEngine;public class TTS : MonoBehaviour {public st…
阅读更多...
基于java 自定义注解Annotation设计简单ORM框架——进阶篇

基于java 自定义注解Annotation设计简单ORM框架——进阶篇

目录 引言实例新建两个注解标注实体类拼接sql语句 总结 引言 一般Java规范编程&#xff08;只是一种习惯&#xff0c;而不是强制&#xff09;中&#xff0c;变量的命名方式一般采用驼峰式命名。比如userName&#xff0c;userImage。但是在数据库中一般不会采用驼峰式&#xff…
阅读更多...
工业物联网解决方案：机房动环监控系统

工业物联网解决方案：机房动环监控系统

工业物联网解决方案&#xff1a;机房动环监控系统 工业物联网&#xff08;IIoT&#xff09;作为数字化转型的关键驱动力&#xff0c;正深刻改变着各行各业的运作模式&#xff0c;其中机房动环监控系统是实现智能化运维管理的重要组成部分。该系统通过集成传感器技术、大数据分…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023