文章目录
- 1.红黑树的概念
- 2.红黑树的几种情况
- 2.1 情况一:cur为红,p为红,g为黑,u存在且为红(p为parent,g为grandfather,u为uncle)
- 2.2 情况二:cur为红,p为红,g为黑,u不存在/u存在且为黑(p为parent,g为grandfather,u为uncle)
- 2.3 情况三:cur为红,p为红,g为黑,u不存在/u存在且为黑(p为parent,g为grandfather,u为uncle)双旋情况
- 3.红黑树的底层
1.红黑树的概念
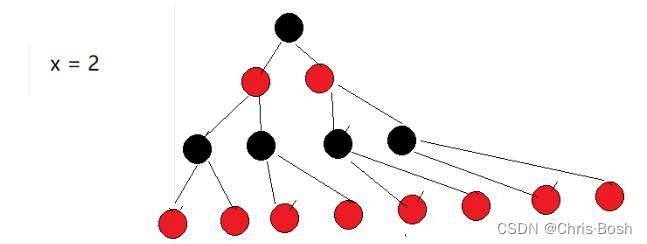
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。
最长路径≤最短路径×2
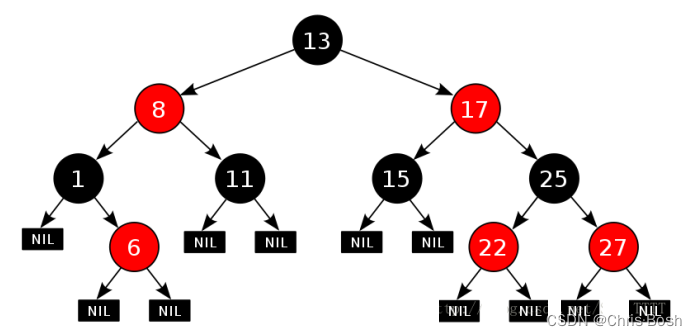
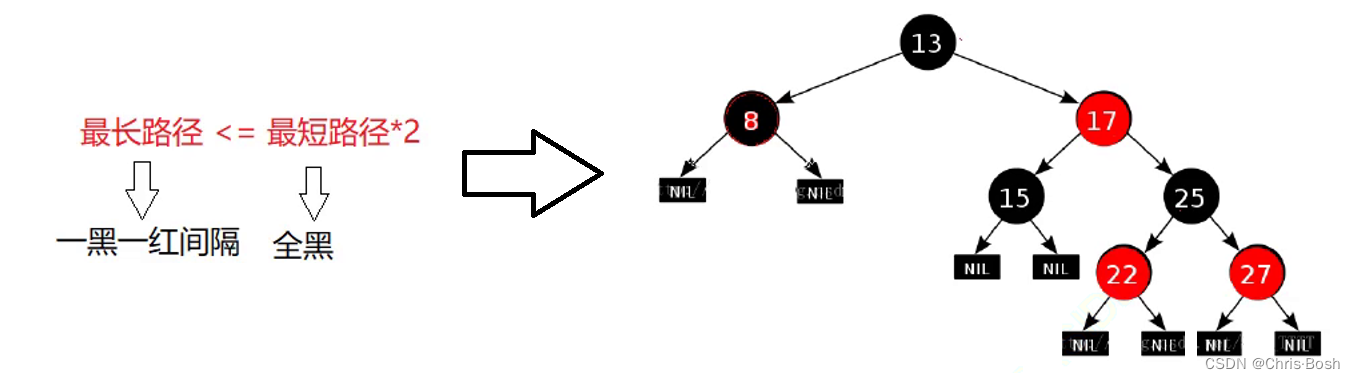
- 每个结点不是红色就是黑色
- 根节点是黑色的
- 如果一个节点是红色的,则它的两个孩子结点是黑色的 (不存在连续的红色节点)
- 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点 (每条路径都存在相同数量的黑色节点)
- 每个叶子结点都是黑色的(此处的叶子结点指的是空结点,不是传统的叶子节点)
2.红黑树的几种情况

2.1 情况一:cur为红,p为红,g为黑,u存在且为红(p为parent,g为grandfather,u为uncle)
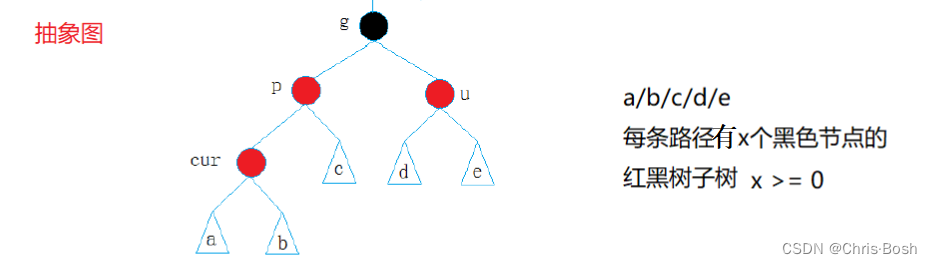
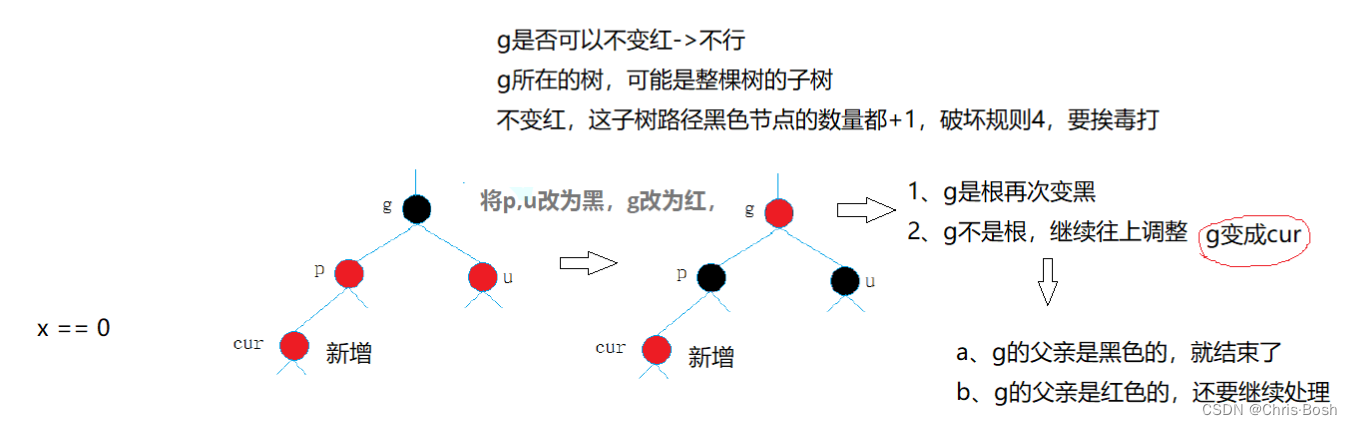
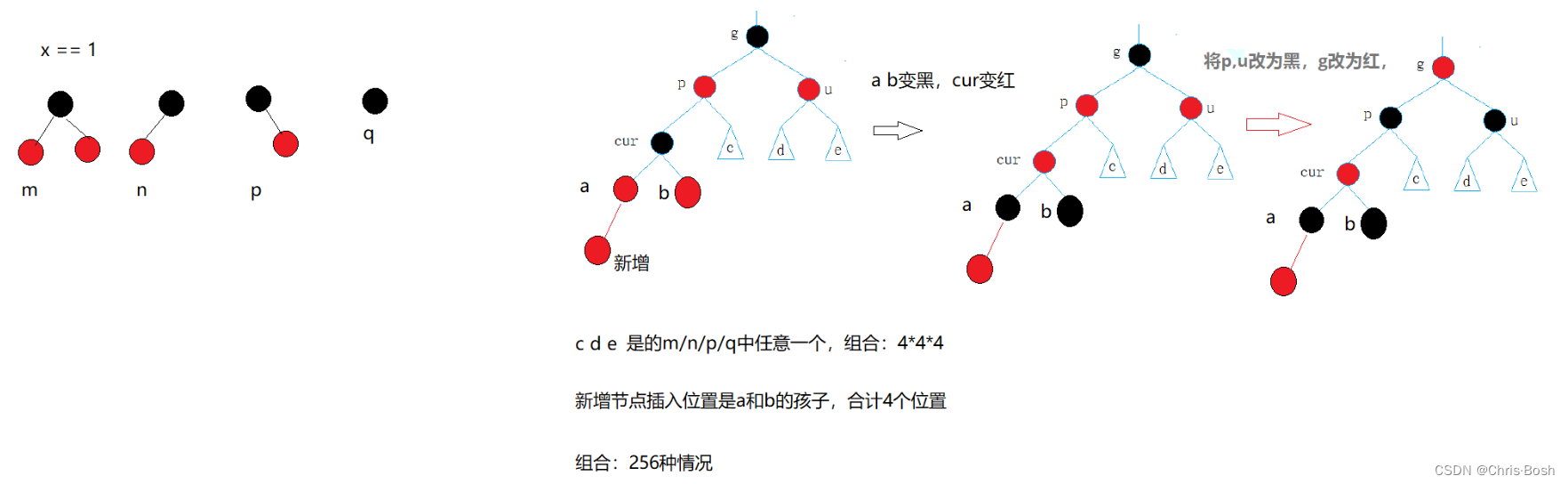
太过复杂
2.2 情况二:cur为红,p为红,g为黑,u不存在/u存在且为黑(p为parent,g为grandfather,u为uncle)
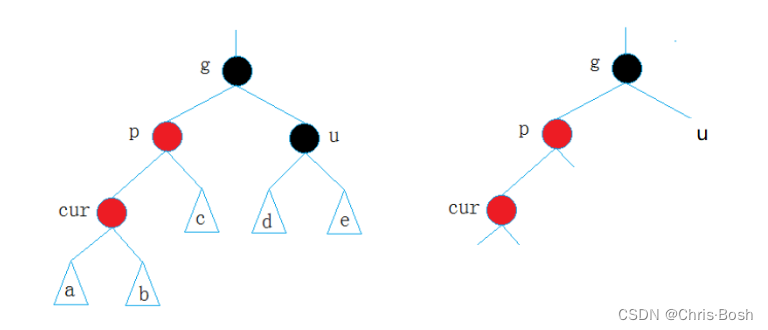
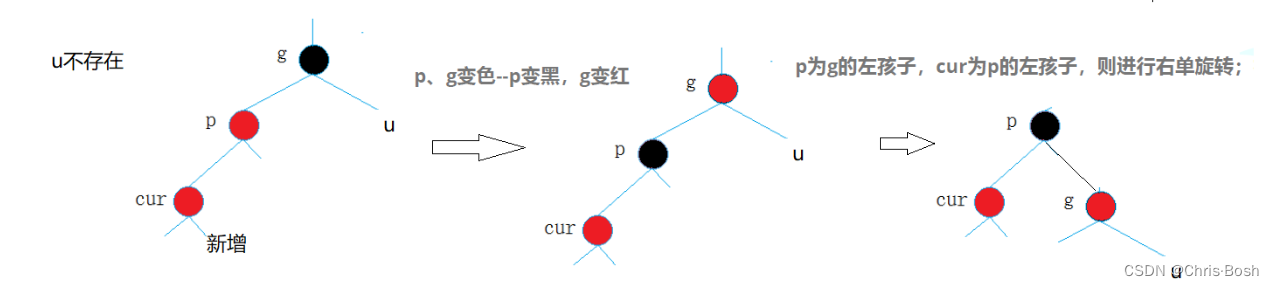
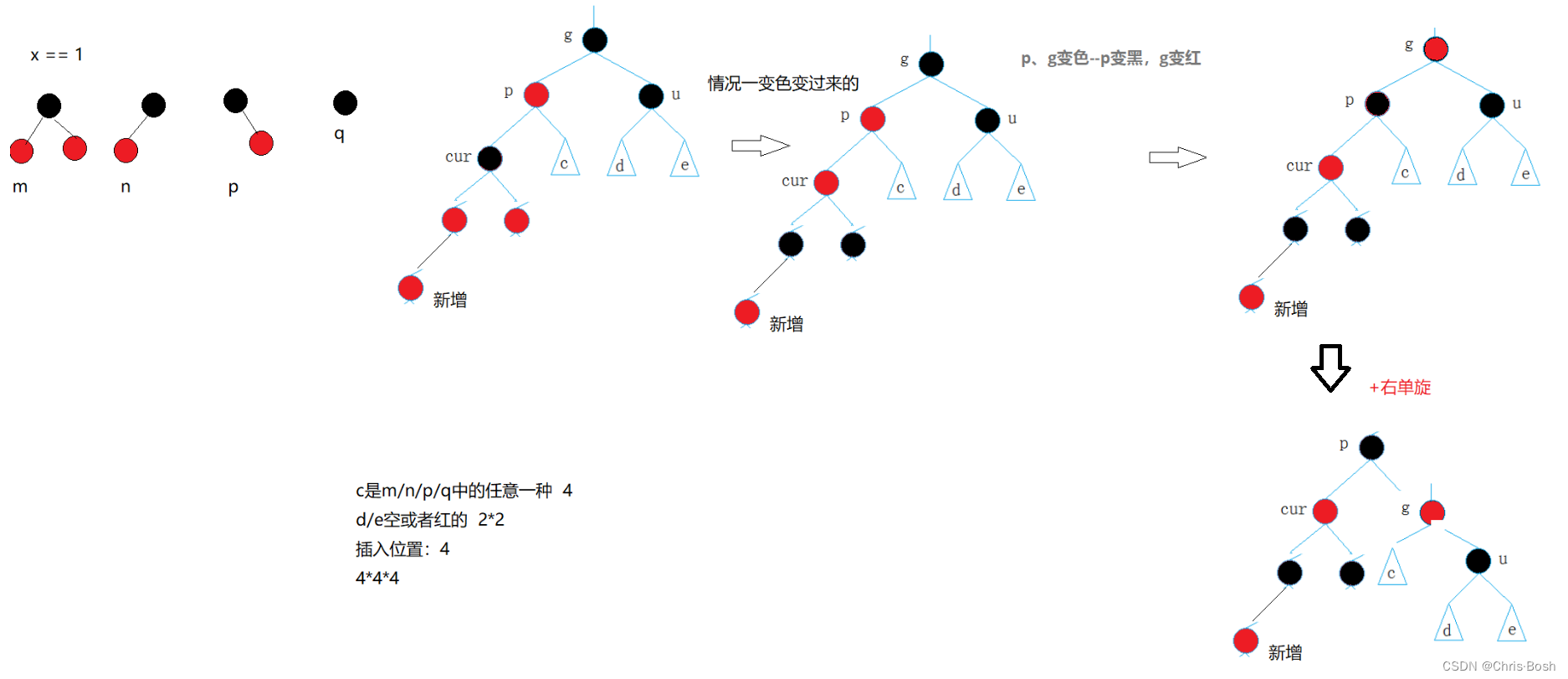
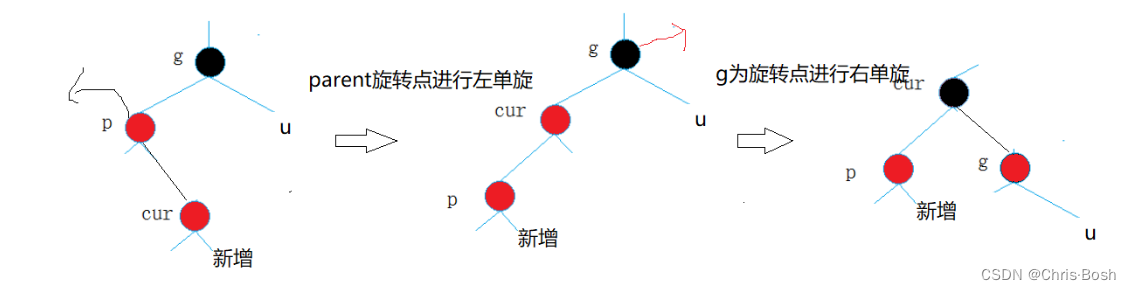
2.3 情况三:cur为红,p为红,g为黑,u不存在/u存在且为黑(p为parent,g为grandfather,u为uncle)双旋情况
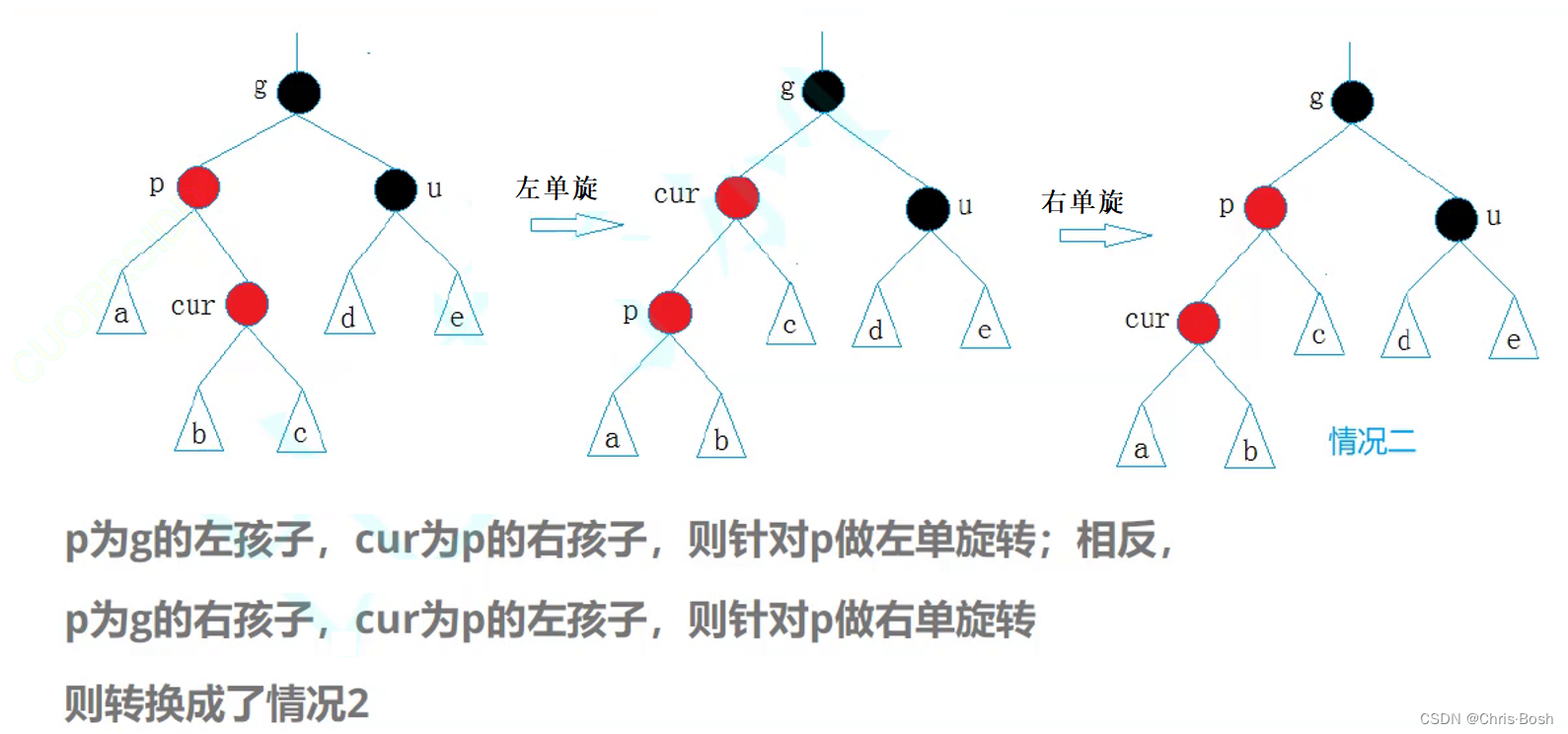
3.红黑树的底层
#pragma once
#include<iostream>
#include<vector>
using namespace std;
enum Colour
{
RED,
BLACK
};
template<class K, class V>
struct RBTreeNode
{
RBTreeNode<K, V>* _left;
RBTreeNode<K, V>* _right;
RBTreeNode<K, V>* _parent;
pair<K, V> _kv;
Colour _col;
RBTreeNode(const pair<K, V>& kv)
:_left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _kv(kv)
, _col(RED)
{}
};
template<class K, class V>
class RBTree
{
typedef RBTreeNode<K, V> Node;
public:
bool Insert(const pair<K, V>& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
_root->_col = BLACK;
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(kv);
cur->_col = RED; // 新增节点给红色
if (parent->_kv.first < kv.first)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent;
// parent的颜色是黑色也结束
while (parent && parent->_col == RED)
{
// 关键看叔叔
Node* grandfather = parent->_parent;
if (parent == grandfather->_left)
{
Node* uncle = grandfather->_right;
// 叔叔存在且为红,-》变色即可
if (uncle && uncle->_col == RED)
{
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
// 继续往上处理
cur = grandfather;
parent = cur->_parent;
}
else // 叔叔不存在,或者存在且为黑
{
if (cur == parent->_left)
{
// g
// p u
// c
//单旋
RotateR(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else
{
// g
// p u
// c
//双旋
RotateL(parent);
RotateR(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
else
{
Node* uncle = grandfather->_left;
// 叔叔存在且为红,-》变色即可
if (uncle && uncle->_col == RED)
{
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
// 继续往上处理
cur = grandfather;
parent = cur->_parent;
}
else // 叔叔不存在,或者存在且为黑
{
// 情况二:叔叔不存在或者存在且为黑
// 旋转+变色
// g
// u p
// c
//单旋
if (cur == parent->_right)
{
RotateL(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else
{
// g
// u p
// c
//双旋
RotateR(parent);
RotateL(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
}
_root->_col = BLACK;
return true;
}
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if (subLR)
subLR->_parent = parent;
subL->_right = parent;
Node* ppNode = parent->_parent;
parent->_parent = subL;
if (parent == _root)
{
_root = subL;
_root->_parent = nullptr;
}
else
{
if (ppNode->_left == parent)
{
ppNode->_left = subL;
}
else
{
ppNode->_right = subL;
}
subL->_parent = ppNode;
}
}
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
if (subRL)
subRL->_parent = parent;
subR->_left = parent;
Node* ppNode = parent->_parent;
parent->_parent = subR;
if (parent == _root)
{
_root = subR;
_root->_parent = nullptr;
}
else
{
if (ppNode->_right == parent)
{
ppNode->_right = subR;
}
else
{
ppNode->_left = subR;
}
subR->_parent = ppNode;
}
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
bool IsBalance()
{
if (_root->_col == RED)
{
return false;
}
int refNum = 0;
Node* cur = _root;
while (cur)
{
if (cur->_col == BLACK)
{
++refNum;
}
cur = cur->_left;
}
return Check(_root, 0, refNum);
}
private:
bool Check(Node* root, int blackNum, const int refNum)
{
if (root == nullptr)
{
//cout << blackNum << endl;
if (refNum != blackNum)
{
cout << "存在黑色节点的数量不相等的路径" << endl;
return false;
}
return true;
}
if (root->_col == RED && root->_parent->_col == RED)
{
cout << root->_kv.first << "存在连续的红色节点" << endl;
return false;
}
if (root->_col == BLACK)
{
blackNum++;
}
return Check(root->_left, blackNum, refNum)
&& Check(root->_right, blackNum, refNum);
}
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
cout << root->_kv.first << ":" << root->_kv.second << ":" << (root->_col == RED ? "RED" : "BLACK") << endl;
_InOrder(root->_right);
}
private:
Node* _root = nullptr;
//size_t _size = 0;
};
void TestRBTree1()
{
//int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };
int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14,8, 3, 1, 10, 6, 4, 7, 14, 13 };
RBTree<int, int> t1;
for (auto e : a)
{
// 1、先看是插入谁导致出现的问题
// 2、打条件断点,画出插入前的树
// 3、单步跟踪,对比图一一分析细节原因
t1.Insert({ e,e });
cout << "Insert:" << e << "->" << t1.IsBalance() << endl;
}
t1.InOrder();
cout << t1.IsBalance() << endl;
}