目录
- 0.原理讲解
- 1.全排列
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
- 2.子集
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
0.原理讲解
- 回溯算法通常⽤于解决组合问题、排列问题和搜索问题等
- 回溯算法的基本思想:
- 从⼀个初始状态开始,按照⼀定的规则向前搜索,当搜索到某个状态⽆法前进时,回退到前⼀个状态,再按照其他的规则搜索
- 回溯算法在搜索过程中维护⼀个状态树,通过遍历状态树来实现对所有可能解的搜索
- 回溯算法的核⼼思想:“试错”
- 在搜索过程中不断地做出选择,如果选择正确,则继续向前搜索
- 否则,回退到上⼀个状态,重新做出选择
- 回溯算法通常⽤于解决具有多个解,且每个解都需要搜索才能找到的问题
- 总结:管他丫的深搜、回溯还是剪枝,画出决策树就完事:P
- 决策树画的越详细越好
- 回溯思考流程
- 决策树
- 设计代码
- 全局变量
DFS()设计
- 细节问题:剪枝、回溯、递归出口
- 注意:没有一成不变的模板,只要能把决策树画出来,把决策树转化成代码就够了
1.全排列
1.题目链接
- 全排列
2.算法原理详解
- 全局变量设计:
vector<vector<int>> ret:存储结果vector<int> path:存储路径vector<bool> check:实现剪枝
DFS()设计思路:仅需关心某一个结点在干什么事情即可- 细节:
- 回溯:
- 剔除
path最后一个元素 - 修改
check数组
- 剔除
- 递归出口:遇到叶子结点的时候,直接添加结果
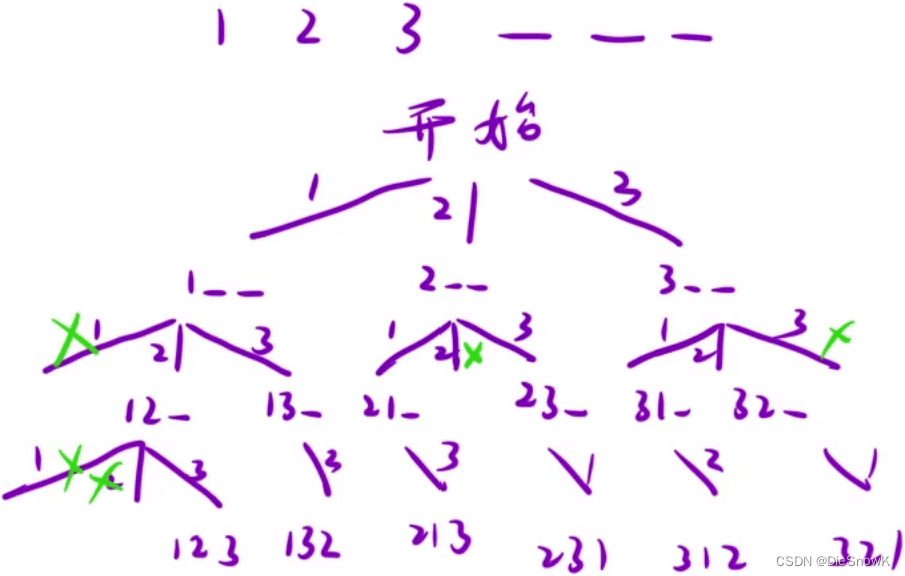
- 回溯:
3.代码实现
class Solution
{
vector<vector<int>> ret;
vector<int> path;
vector<bool> check; // 实现剪枝
public:
vector<vector<int>> permute(vector<int>& nums)
{
check.resize(nums.size(), false);
DFS(nums);
return ret;
}
void DFS(vector<int>& nums)
{
if(nums.size() == path.size())
{
ret.push_back(path);
return;
}
for(int i = 0; i < nums.size(); i++)
{
if(!check[i])
{
path.push_back(nums[i]);
check[i] = true;
DFS(nums);
// 回溯 -> 恢复现场
path.pop_back();
check[i] = false;
}
}
}
};
2.子集
1.题目链接
- 子集
2.算法原理详解
-
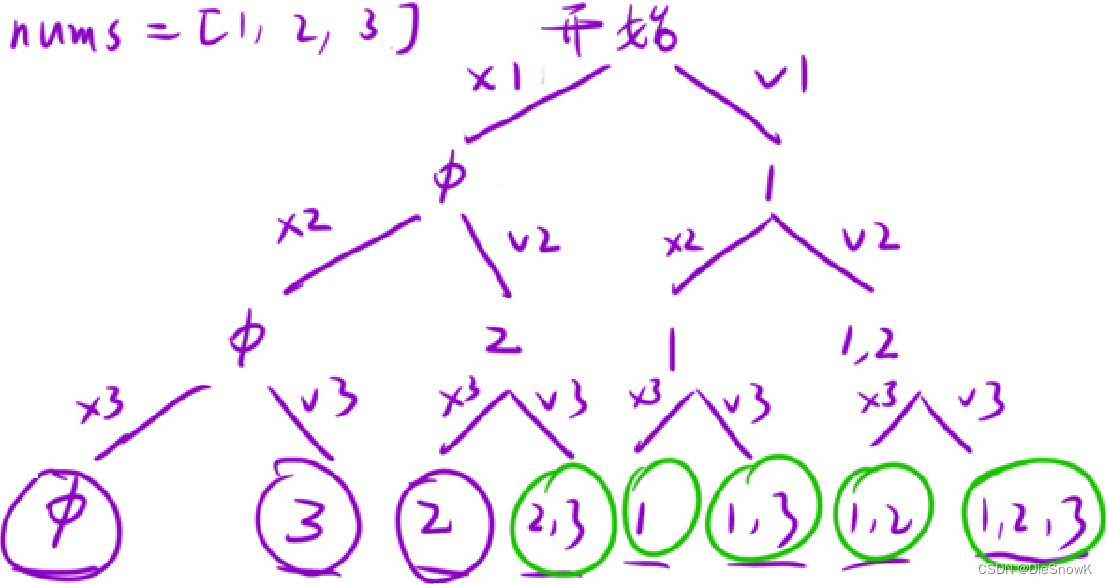
思路一:每次盯着一个数,选或是不选
- 全局变量:
vector<int> pathvector<vector<int>> ret
DFS()设计- 函数头:
void DFS(nums, i)i:下一层递归要选的元素
- 函数体:
- 选:
path += nums[i], DFS(num, i + 1) - 不选:
DFS(nums, i + 1)
- 选:
- 递归出口:
i == nums.size()
- 函数头:
- 回溯:选时需要回溯
- 全局变量:
-
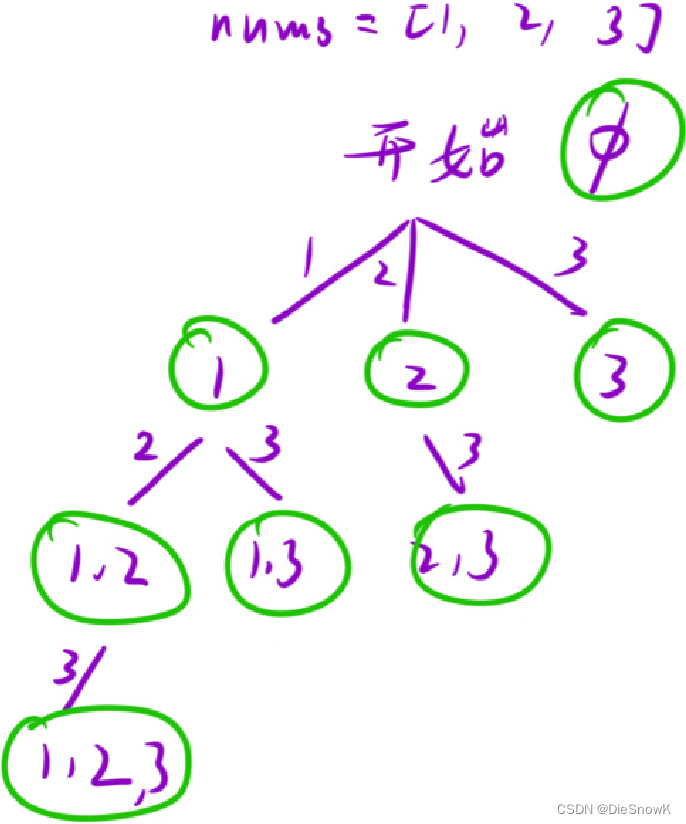
思路二:每次都只选一个数,此后只能选它后面的数
- 全局变量:
vector<int> pathvector<vector<int>> ret
DFS()设计- 函数头:
void DFS(nums, pos)pos:下一层递归选择数时的起始下标
- 函数体:
- 循环枚举还能选哪些数
- 递归出口:不需要特定函数出口
- 函数头:
- 回溯:函数返回时回溯
- 全局变量:
-
思路二是优于思路一的
- 思路二每次递归,都会是一个结果,而思路一结果只会出现在叶子节点上
- 思路二递归的次数是要明显少于思路一的
3.代码实现
// v1.0 每次盯着一个数,选或是不选
class Solution
{
vector<vector<int>> ret;
vector<int> path;
public:
vector<vector<int>> subsets(vector<int>& nums)
{
DFS(nums, 0);
return ret;
}
void DFS(vector<int>& nums, int i)
{
if(i == nums.size())
{
ret.push_back(path);
return;
}
// 选
path.push_back(nums[i]);
DFS(nums, i + 1);
path.pop_back(); // 回溯,恢复现场
// 不选
DFS(nums, i + 1);
}
};
----------------------------------------------------------------------------------
// v2.0 每次都只选一个数,此后只能选它后面的数
class Solution
{
vector<vector<int>> ret;
vector<int> path;
public:
vector<vector<int>> subsets(vector<int>& nums)
{
DFS(nums, 0);
return ret;
}
void DFS(vector<int>& nums, int pos)
{
ret.push_back(path);
for(int i = pos; i < nums.size(); i++)
{
path.push_back(nums[i]);
DFS(nums, i + 1);
path.pop_back(); // 回溯,恢复现场
}
}
};

![[FSCTF 2023]ez_php1](https://img-blog.csdnimg.cn/direct/f48e58a5f88648738d960fd59130d929.png)