目录
常见位运算总结
位运算相关算法题
1. 只出现一次的数字
2. 只出现一次的数字(|||)
3. 两整数之和
4. 只出现一次的数字(||)
常见位运算总结
在开始刷位运算这个类型的题目前,我想先带着大家学习一下一些常见的基础运算操作,我们后面刷题时对题目的处理都是基于这些基本运算。
1. 基础位运算
想必大家对位运算符都是非常熟悉的,在这里,我为大家讲讲我对几个按位操作符的理解
&:有0就是0
| :有1就是1
^ :相同为0,相反为1 (也可以视作为无进位相加)
2. 给一个数n,确定二进制表示中第x位是0还是1
(n >> x) & 1
3. 将一个数n的二进制表示的第x位修改成1
n |=(1 << x)
4. 将一个数n的二进制表示的第x位修改成0
n &= (~(1 << x))(~就是取反)
5. 位图的思想
位图的本质就是个哈希表,我们先前学习过的哈希表在大部分情况下都是数组形式的
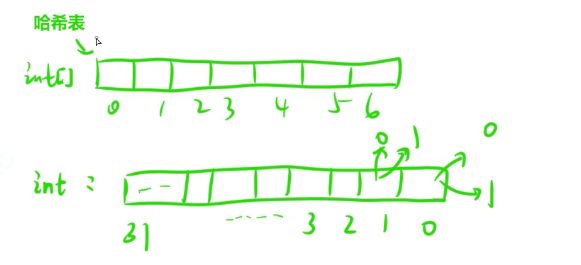
使用一个变量的比特位来记录信息,对哈希表的增删查改,就相当于是对比特位的增删查改,这就意味着,我们前面讲到的几种常见的位运算操作都是非常重要的,能帮助我们更好地操作位图
6. 提取一个数n最右侧的1
这个描述听起来有些抽象,我为大家举个例子:

这就是提取最右侧的1
操作方式:n & -n
-n是由n按位取反再+1得到的:
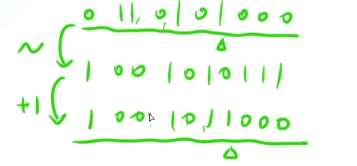
通过这个例子我们发现了:n与-n的关系是,在最右侧的1的左侧,n与-n完全相反;在最右侧的1的右侧,n与-n完全相同。则左侧区域两者&的结果必定为0,右侧区域&的结果不变,于是我们实现了把最右侧1提取出来的操作。
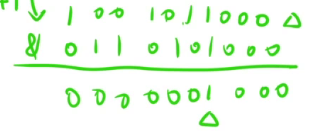
7. 干掉一个数n二进制表示中最右侧的1
n & (n - 1)

众所周知,减法是存在借位的,n - 1的本质就是,将最右侧的1右侧的区域全部取反

8. 异或运算的运算律

现在我们已经学习完了常见的操作,接下来开始刷题吧!大家可以先试着做以下几道题练练手,根据我们的总结可以直接处理:
191. 位1的个数 - 力扣(LeetCode)
461. 汉明距离 - 力扣(LeetCode)
接下来我们来另外刷下这几道题。希望大家在看讲解前,先自己动手编写代码,实在没有思路时再去看答案,这样才能实际提高水平~
位运算相关算法题
1. 只出现一次的数字
136. 只出现一次的数字 - 力扣(LeetCode)
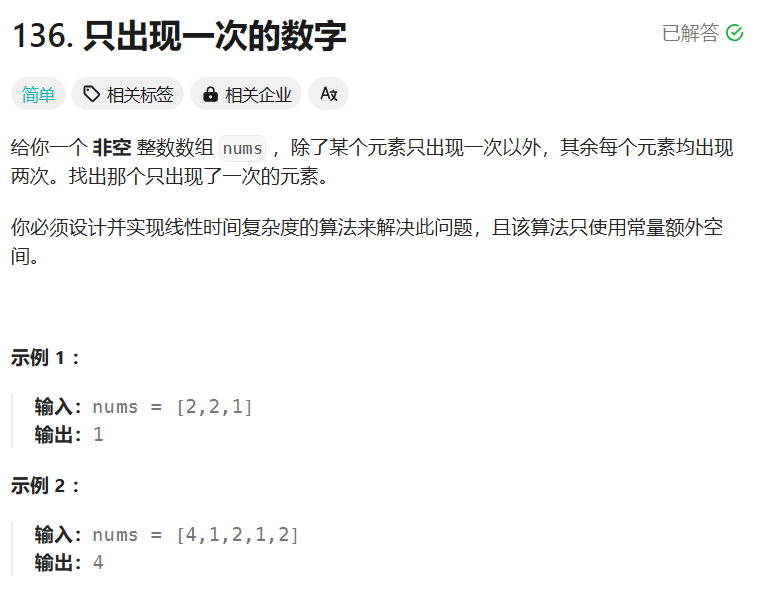
题目解析:
这道题目如果我们没有学习过位运算,可能只能想到创建一个哈希表,通过哈希表来找到只出现一次的元素。但事实上,根据我们在常见位运算总结中的第八点:任何书亦或0的结果为这个数本身、两数相同时为0、异或运算满足结合律,我们可以得出一个结论:在数组中出现了两次的元素可以结合为0,因为只出现了一次的元素只有一个,所以我们对整个数组求亦或和,得到的结果就是只出现一次的元素!
代码:
class Solution {
public:
int singleNumber(vector<int>& nums)
{
int k = 0;
for(auto num : nums)
{
k ^= num;
}
return k;
}
};2. 只出现一次的数字(|||)
260. 只出现一次的数字 III - 力扣(LeetCode)

题目解析:
本题如果使用哈希表,可以非常轻松的解决,但由于面试中,面试官可能会问我们有没有其他的解法,所以我们这里试着用位运算来处理。本题与上一题的区别在于,仅出现一次的元素有两个,我们就不能简单地求整个数组的亦或和,而是要试着把这两个数字分离开。
我们依然先求出整个数组的亦或和sum,因为两个数字都是只出现一次的,所以sum的比特位必定有一位是1,因为sum可以被视为是两个数字亦或得到的,所以sum的每个为1的比特位对应的都是两个数字相异的比特位!这正好符合我们要将这唯二两个只出现一次的数字分离开的需求,所以接下来我们只需要提取出sum中的一个1,与整个数组相与就能把两个数字分离了,在常见位运算总结中,我们学到了提取最右侧1的方法:n&-n,所以我们可以轻松提取出sum的最右侧的1,根据这个作为条件进行判断即可。
大家可能会奇怪,我只提到了分离这两个只出现一次的数字,那出现两次的呢?当然是因为对于出现两次的数字,在条件判断时,两个都会被分到其中的一组,则我们接下来对这两组元素分别求亦或和,就能分别得到两个只出现一次的数字了。
class Solution {
public:
vector<int> singleNumber(vector<int>& nums)
{
int orsum = 0;
for(auto num : nums)
{
orsum ^= num;
}
int jud = (orsum == INT_MIN) ? orsum : orsum & (-orsum);
int type1 = 0, type2 = 0;
for(auto num : nums)
{
if(num & jud)
{
type1 ^= num;
}
else
{
type2 ^= num;
}
}
return {type1, type2};
}
};3. 两整数之和
371. 两整数之和 - 力扣(LeetCode)

题目解析:
本题乍一看无从下手,但是其实可以用我们总结的位运算操作来实现,还记得么,亦或运算实际上就是无进位相加,那么我们只要把两个数的亦或和加上他的进位就行了。
至于进位,运算时仅当两个比特位都为1时才产生进位,是不是让我们联想到了与运算,仅当两个比特位都为1时才为1,由于进位的结果要加到更高的比特位上,所以我们将两个数的按位与之和左移一位,得到的就是本次相加的进位,接下来把进位、无进位相加结果相加即可。
可是这不就又涉及到相加了吗?所以我们要重复这个流程,运算中不再有进位为止,这样就实现了不适用+、-进行两个整数的相加。
还有一个细节问题,有符号整数在内存中是以补码的形式存储的,对于补码的运算规则是:
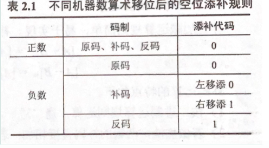
对于补码的移位运算,如果他的最高位与符号位是不一样的,左移的时候就会出现问题,举个例子:
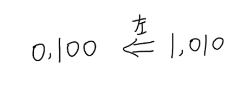
此时我们发现,这个数左移时,符号位发生了变化,也就是说我们的左移操作是有问题的,为了避免这种情况,我们使用unsigned int来代替int进行储存变量
class Solution {
public:
int getSum(int a, int b)
{
while(b)
{
int x = a ^ b;
unsigned int carry = (unsigned int)(a & b) << 1;
a = x;
b = carry;
}
return a;
}
};4. 只出现一次的数字(||)
LCR 004. 只出现一次的数字 II - 力扣(LeetCode)

题目解析:
本题和前面两道只出现一次的数字一样,都可以用哈希表来非常轻松的解决,但是如果要求不使用额外空间来实现的话,就要用到位图了。
依据题意,给定的元素可以被分为两类:出现一次的元素、出现三次的元素,对于整型数的32个比特位的每一位而言,可能的取值为0、1,则如果我们求这两类元素某一个比特位的和,由于第二类元素都出现了三次,假设nums范围为[0, n],则这类元素的和一定等于3 * m(m <= n).
至于只出现一次的元素,在该比特位可能为0、1,所以对所有元素来说,该比特位的和可能值为:3 * m、3 * m + 1,对这个结果取模3,得到的可能结果为0、1,这正是只出现一次的元素的这一比特位,所以我们可以依法炮制,求出所有比特位。
至于判断某个比特位是否为1、将某个比特位修改为1的方式,我们都在常见位运算总结部分提到了,所以直接上手写代码:
class Solution {
public:
int singleNumber(vector<int>& nums)
{
int ret = 0;
for(int i = 0; i < 32; i++)
{
int sum = 0;
for(auto &num : nums)
{
if((num >> i) & 1) sum++;
}
// 如果比特位和模3余1,将返回值的该比特位修改为1
if(sum % 3 == 1)
ret |= (1 << i);
}
return ret;
}
};