参考视频:https://www.bilibili.com/video/BV1ko4y1P7Zv/?spm_id_from=333.337.search-card.all.click&vd_source=7a1a0bc74158c6993c7355c5490fc600
如下图所示,马尔可夫链条实际上就是 “状态机”,只不过状态机里不同状态之间的边上是 “概率”
马尔可夫链有一个非常好的性质,那就是:所有 next state 都只和 current state 有关
所以,计算概率的时候,条件只有当前状态
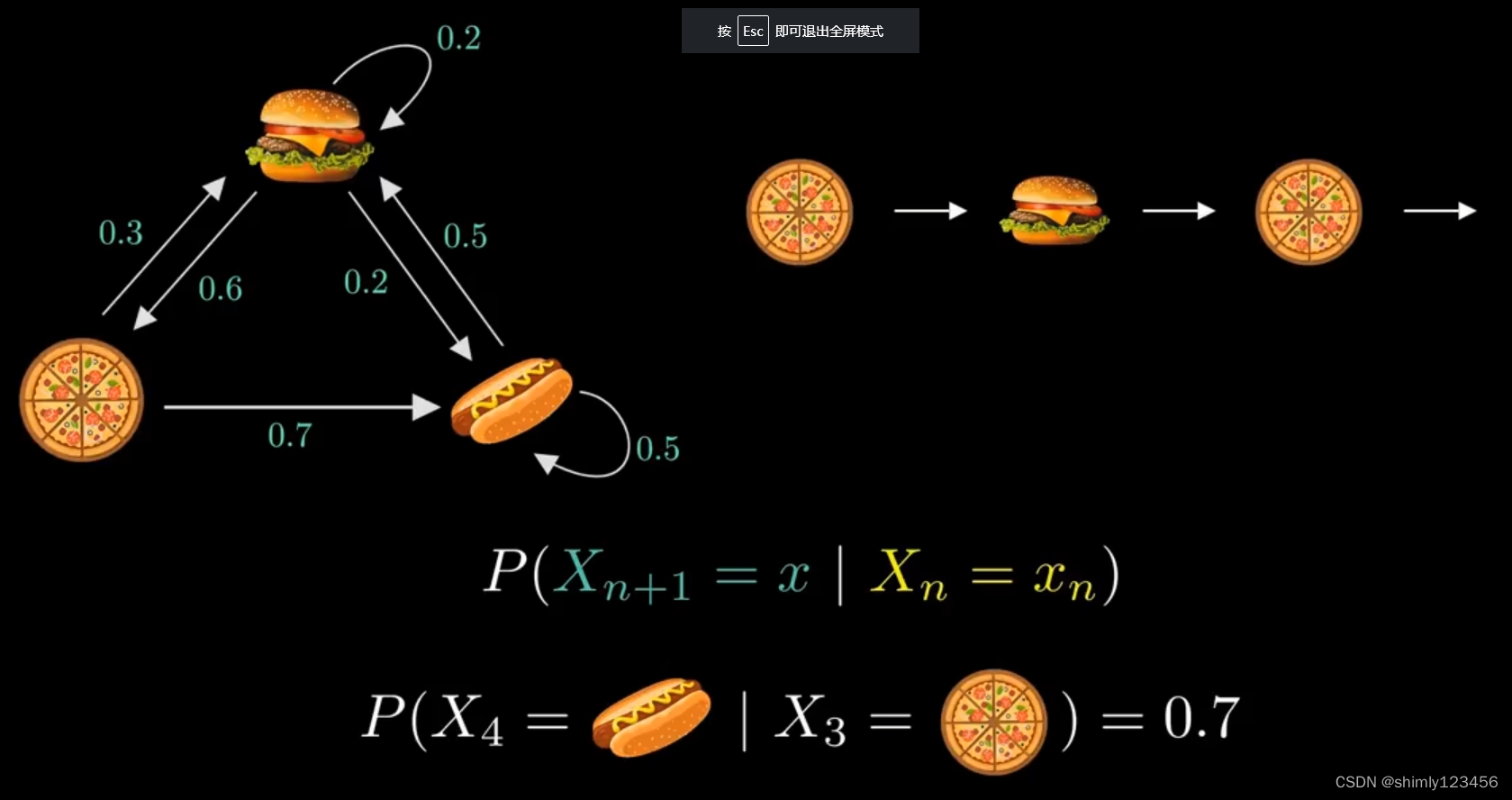
一个很自然的想法是:马尔可夫链是否有 “稳态”?
也就是说,当链条足够长时,链条上出现的不同状态是否会收敛于某个比例
经过试验统计,比如 100W 长度的链条,发现确实会收敛于某个比例
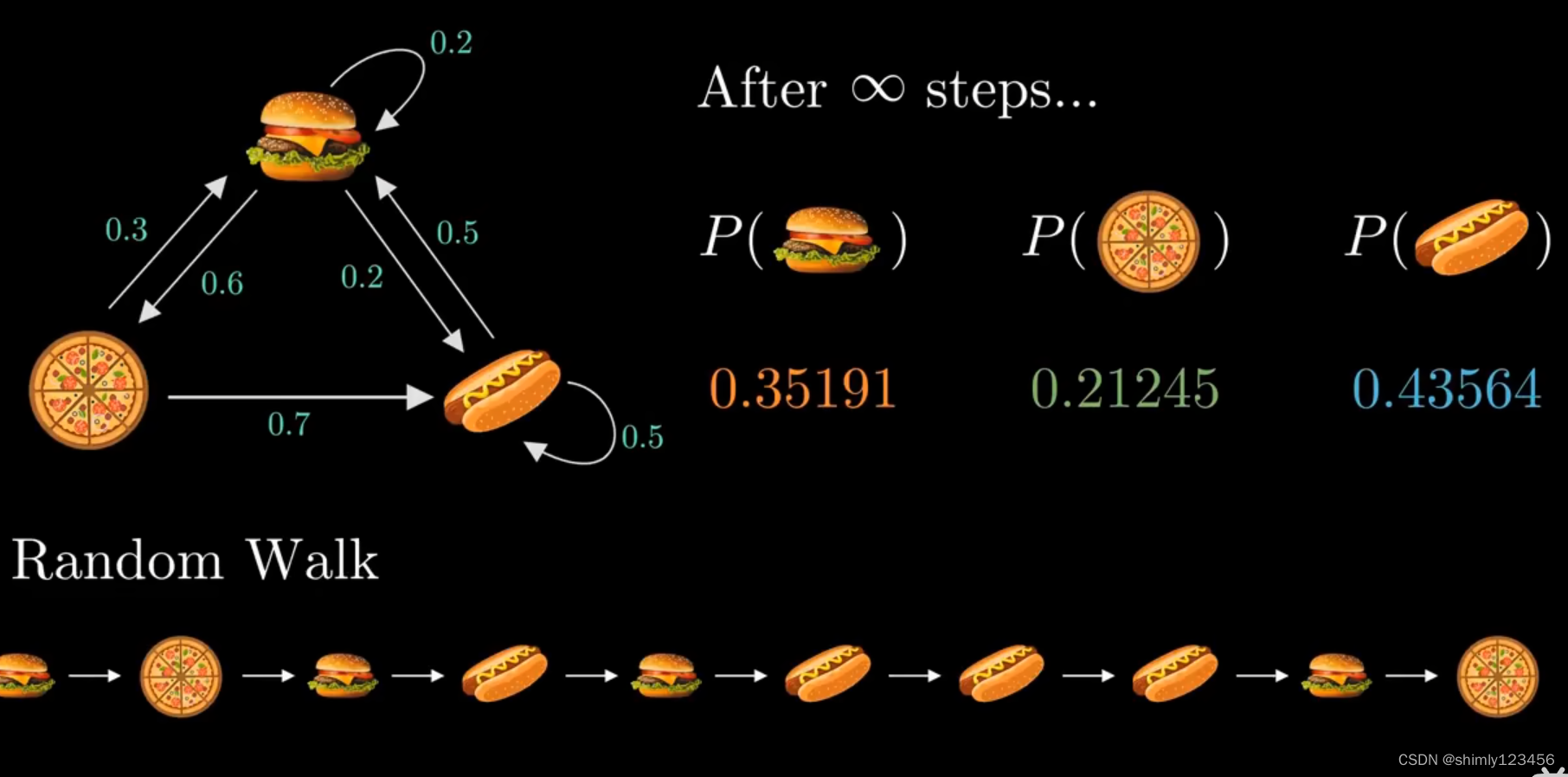
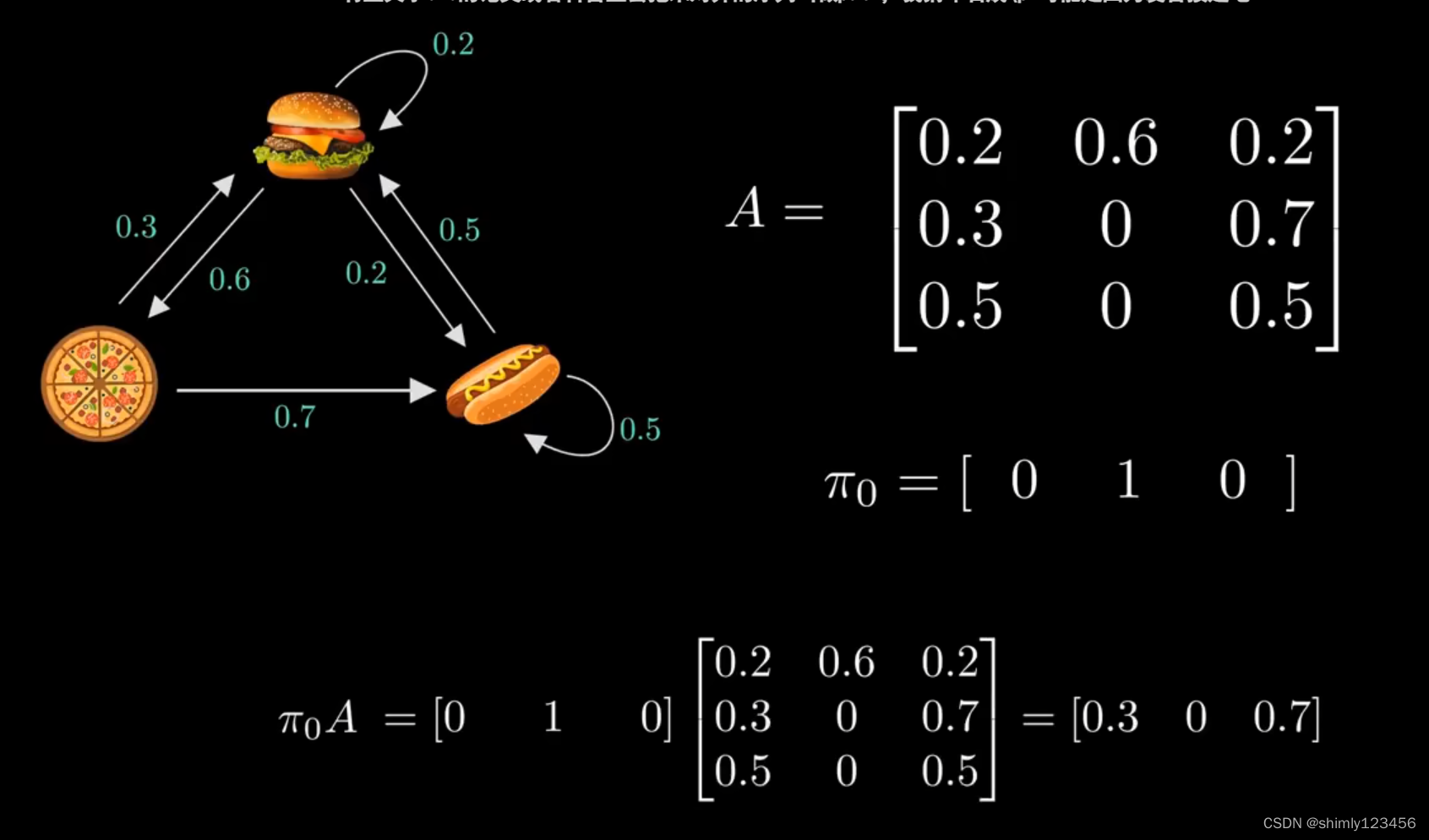
那么是否可以通过计算得到 “稳态” 呢?是可以的,如下图,分别是转移矩阵 A,和状态概率矢量 pi
通过让状态概率矢量 pi 和转移矩阵A 相乘,我们可以得到披萨状态的未来概率。(披萨状态用 [0 1 0] 表示)
此时,我们可以把 [0.3 0 0.7] 表示为 pi1,随后用 pi1 x A 来计算 pi2
如果存在稳态,用 pi 表示,那么有 pi x A = pi。此时一看,卧槽,这个 pi 不是特征值为 1 的特征向量嘛?
此时还有另外一个条件:pi 的所有元素加起来必须等于 1,因为每一个元素代表一个东西的概率
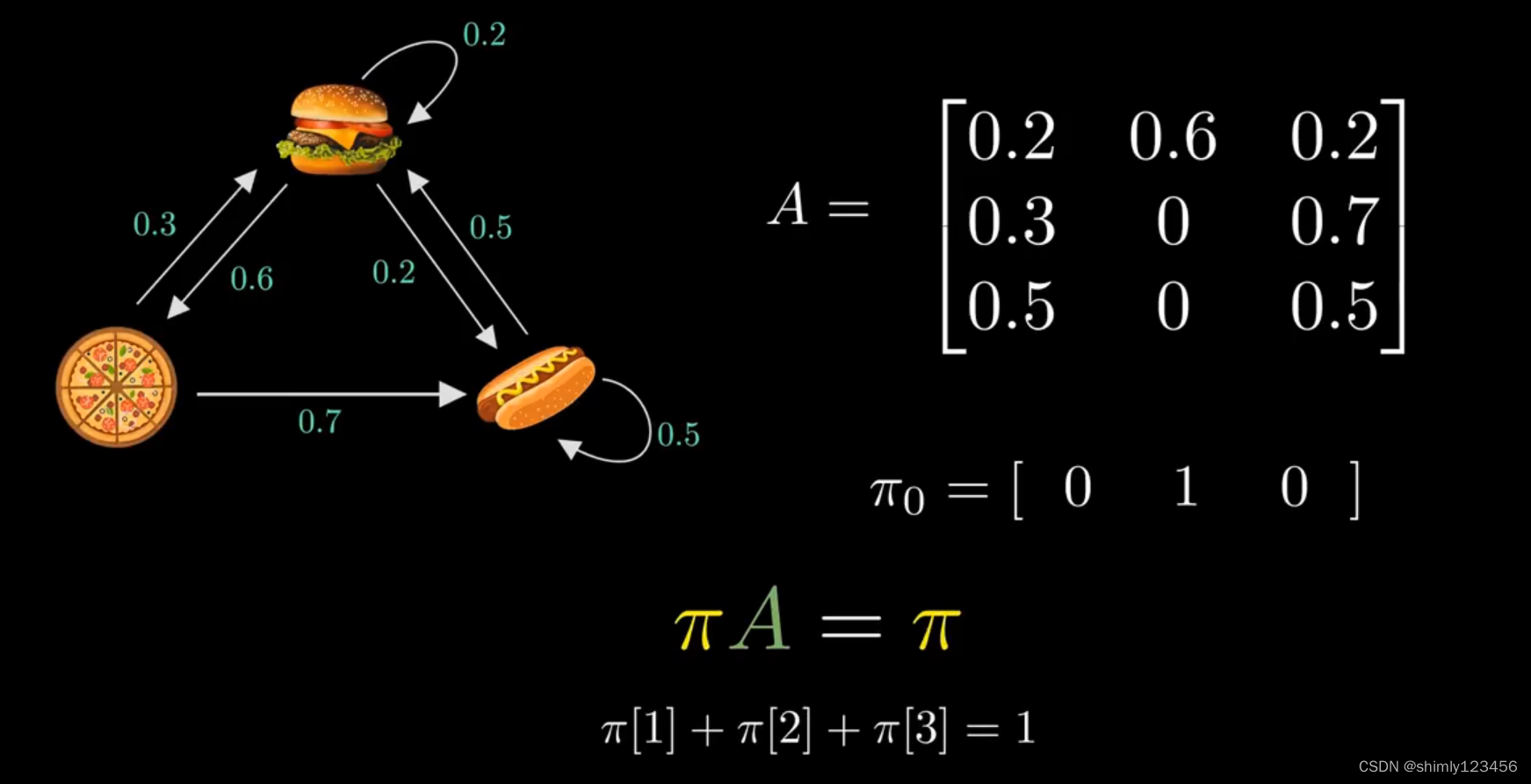
于是,有两个等式,如下图
于是,有两个等式,如下图,分别是:
1.pi x A = pi
2.pi[1] + pi[2] + pi[3] = 1
解完这两个等式后,我们得到了下图的内容,就是 “稳态”
如下图,是通过两个式子计算出的 “稳态”。
那么,有可能存在多个 “稳态” 嘛?答案是肯定的,我们只需要看一下是否存在不止一个特征值等于1的特征向量即可