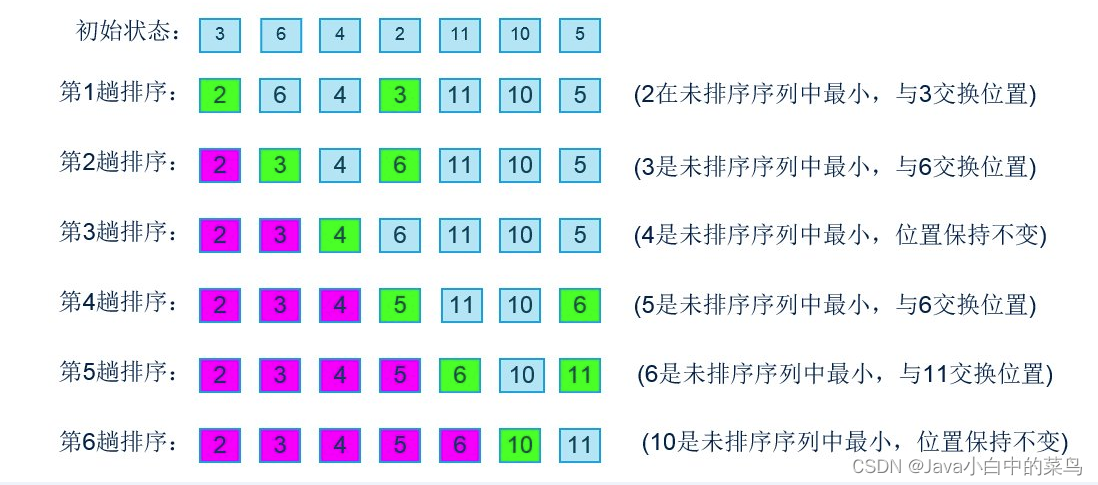
选择排序(selection sort)的工作原理非常简单:开启一个循环,每轮从未排序区间选择最小的元素,将其放到已排序区间的末尾。选择排序的主要特点包括:
-
时间复杂度:
- 无论最好、最坏还是平均情况,选择排序的时间复杂度均为O(n^2),其中n是列表长度。这是因为每一轮都需要遍历剩余的未排序元素来寻找最小值,共需进行n-1轮比较。
-
空间复杂度:
- 选择排序是原地排序算法,除了用于交换的临时变量外,不需要额外的存储空间,因此其空间复杂度为O(1)。
-
稳定性:
- 选择排序不是稳定的排序算法。如果数组中有相等的元素,它们的原始顺序可能会在排序后发生变化,因为选择排序只保证找到当前未排序部分的最小值,并不关心相等元素之间的相对位置。
-
算法步骤:
- 初始化一个指示最小值位置的变量。
- 遍历数组,找到当前未排序部分的最小值(或最大值,取决于升序还是降序)。
- 将找到的最小值与未排序部分的第一个元素交换位置。
- 重复上述两步,直到整个数组排序完成
选择排序的Java代码实现如下:
/* 选择排序 */
void selectionSort(int[] nums) {
int n = nums.length;
// 外循环:未排序区间为 [i, n-1]
for (int i = 0; i < n - 1; i++) {
// 内循环:找到未排序区间内的最小元素
int k = i;
for (int j = i + 1; j < n; j++) {
if (nums[j] < nums[k])
k = j; // 记录最小元素的索引
}
// 将该最小元素与未排序区间的首个元素交换
int temp = nums[i];
nums[i] = nums[k];
nums[k] = temp;
}
}选择排序的算法流程如图所示: