星期一:
dp题单 区间dp第三题 二叉搜索树 cf传送门

思路:dp【i】【j】【0/1】表示区间 i到 j,以 i / j为根节点能否形成一棵二叉搜索树
因为题目要求组成二叉搜索树,若 i 到 j 的节点为一颗完整的子树时有合法的构造方案,那么其根节点一定为 i-1 或 j+1,所以转移时先枚举区间 l r,再枚举区间内的点 k,若以 k 为根( l 到k-1为其左子树,k+1到 r为其右子树)有合法的构造方案,且 k与 l-1 或 r+1的gcd合法,则 l-1 到 r 或 l 到 r+1存在合法构造
代码如下:
ll n;
int a[770];
int dp[770][770][2];
bool gc[770][770];
void solve(){
cin >> n;
for(int i=1;i<=n;i++) cin >> a[i];
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++)
gc[i][j]=(__gcd(a[i],a[j])!=1); //预处理
}
for(int i=1;i<=n;i++) dp[i][i][0]=dp[i][i][1]=1;
for(int len=1;len<=n;len++){
for(int l=1;l+len-1<=n;l++){
int r=l+len-1;
for(int k=l;k<=r;k++){
if(dp[l][k][1] && dp[k][r][0]){
if(gc[l-1][k]) dp[l-1][r][0]=1;
if(gc[k][r+1]) dp[l][r+1][1]=1;
}
}
}
}
for(int i=1;i<=n;i++){
if(dp[1][i][1] && dp[i][n][0]){cout << "Yes"; return ;}
}
cout << "No";
}dp题单 区间dp 第四题 分三角形 cf传送门

初见低级贪心题,再一细看,嗯?区间dp好题!
正解(不解释:
ll n;
void solve(){
cin >> n;
ll ans=0;
for(int i=2;i<n;i++) ans+=i*(i+1);
cout << ans;
}而如果题目给多边形的每个点赋上权值,贪心可能就会失效,只能用下面的区间dp
思路:dp【i】【j】表示考虑 i 到 j区间最低权值
长度从3开始枚举,假设已知 i 到 k区间和 j 到 k区间的最低价值,i 到 j区间的最低价值即可能为 dp[ i ][ k ]+dp[ k ][ j ]+i*j*k,相当于 在 i,j 间连条边,形成端点为 i,j,k的三角形
代码如下:
ll n;
ll dp[550][550];
void solve(){
cin >> n;
for(int i=1;i<=n;i++)
for(int j=i+2;j<=n;j++) dp[i][j]=1e18; //初始化记得j从i+2开始
for(int len=3;len<=n;len++){
for(int l=1;l+len-1<=n;l++){
int r=l+len-1;
for(int k=l+1;k<r;k++)
dp[l][r]=min(dp[l][k]+dp[k][r]+l*r*k,dp[l][r]);
}
}
cout << dp[1][n];
}星期二:
dp题单 背包 第五题 军队排列 cf传送门

题意:n1个步兵,n2个骑兵,步兵不能连续站超过k1个,骑兵不能连续超过k2个,问排列方案数
思路:dp【i】【j】【k】【0/1】表示已经站了 i个步兵,j个骑兵,尾部是连续 k个步/骑的方案数,转移如下
代码如下:
const int mod=1e8;
ll n;
ll n1,n2,k1,k2;
ll dp[110][110][11][2];
void solve(){
cin >> n1 >> n2 >> k1 >> k2;
dp[1][0][1][0]=1,dp[0][1][1][1]=1;
for(int i=0;i<=n1;i++){
for(int j=0;j<=n2;j++){
if(i>0){
for(int k=2;k<=k1;k++)
dp[i][j][k][0]=dp[i-1][j][k-1][0]; //步兵后跟步兵
for(int k=1;k<=k2;k++)
dp[i][j][1][0]+=dp[i-1][j][k][1],dp[i][j][1][0]%=mod; //骑兵之后放步兵
}
if(j>0){
for(int k=2;k<=k2;k++)
dp[i][j][k][1]=dp[i][j-1][k-1][1]; //骑兵后跟骑兵
for(int k=1;k<=k1;k++)
dp[i][j][1][1]+=dp[i][j-1][k][0],dp[i][j][1][1]%=mod; //步兵后跟骑兵
}
}
}
ll ans=0;
for(int k=1;k<=k1;k++) ans+=dp[n1][n2][k][0],ans%=mod;
for(int k=1;k<=k2;k++) ans+=dp[n1][n2][k][1],ans%=mod;
cout << ans;
}下午队内赛
补队内赛E cf传送门

思路:没看出来是分类讨论,6是特判-1
首先如果 x是奇数,将其分为x/2,x/2+1,一定满足互质且差最小,为1
x为偶数,若x/2为偶数,可分为x/2+1和x/2-1,差为2,而若x/2为奇数,可考虑分为x/2+2和x/2-2,但可能还有比4更好的分法
若x是3的倍数,能将其分为x/3-1,x/3,x/3+1的形式,为奇偶奇,差为2
若x%3==1,分为x/3-1,x/3,x/3+2,偶奇奇,差为3,注意特判若x/3-1为3的倍数,则不能这样分
若x%3==2,分为x/3-1,x/3+1,x/3+2,奇奇偶,差为3,同上,注意特判
代码如下:
void solve(){
int tt; cin >> tt;
for(int ii=1;ii<=tt;ii++){
int x; cin >> x;
cout << "Case #" << ii << ": ";
if(x==6){cout << "-1\n"; continue;}
if(x&1){cout << "1\n"; continue;}
if((x/2-1)&1) cout << "2\n";
else{
if(x%3==0) cout << "2\n";
else{
if(x%3==1){
if((x/3-1)%3==0) cout << "4\n";
else cout << "3\n";
}else{
if((x/3-1)%3==0) cout << "4\n";
else cout << "3\n";
}
}
}
}
}星期三:
上午和队友vp了把23广东省赛,时间关系只打了4h,5题500罚时
记录 I 题 cf传送门

思路:涉及一点 stl 操作,还有multiset是个不错的容器,可以存放pair,再扩展下可以存结构体,在结构体里重写排序运算符,即可实现自定义的二分查找
代码如下:
ll n;
int m;
void solve(){
cin >> n >> m;
unordered_map<int,PII>mp;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
int x; cin >> x;
mp[x]={i,j}; //存放每个点的坐标
}
}
multiset<PII>mt;
mt.insert({1,1}),mt.insert({n,m});
mt.insert({0,0}); //防止查找第一行的坐标时,pit会成为野指针
for(int i=0;i<=n*m-1;i++){
int x=mp[i].first,y=mp[i].second;
auto it=mt.lower_bound({x,y});
auto pit=prev(it);
int y11=pit->second;
int y2=it->second;
if(y>=y11 && y<=y2) mt.insert({x,y}); //判断是否在可走范围内
else{cout << i << "\n"; return ;}
}
cout << n*m << "\n";
}K因为os忘记多个样例清空数组,耽误了1h且惨遭3发罚时(警钟长鸣!!!
补星期二队内赛 F cf传送门

思路:4e4内的回文数很少,先全算出来,dp【x】表示组成 x的方案数,用完全背包写法
刚开始想了很久没想明白是如何进行转移的,为何可以这样转移
dp【i】【j】代表用前 i个回文数组成 j的方案数
转移方程为dp【i】【j】=dp【i-1】【j】+dp【i】【j-a [ i ]】,后俩表示用前 i-1个回文数组成 j的方案数 加上 用至少1个a【i】组成 j的方案数,再滚动一下
代码如下:
void solve(){
vector<int>a;
vector<ll>dp(4e4+1);
for(int i=1;i<=4e4;i++){
string s=to_string(i);
string ss=s; reverse(ss.begin(),ss.end());
if(s==ss) a.push_back(i);
}
dp[0]=1;
for(auto i:a){
for(int j=i;j<=4e4;j++) dp[j]+=dp[j-i],dp[j]%=mod;
}
int t; cin >> t;
while(t--){
int x; cin >> x;
cout << dp[x] << "\n";
}
}补cf round943 div3 E cf传送门

思路:能想到在 n>=4 时曼哈顿距离能拿满,那么怎么拿呢
在主对角线放n-2个,剩下两个一个放 n-1,n,一个放 n,n,前者负责奇数曼哈顿距离,后者偶数(这也能扯到奇偶性?
代码如下:
void solve(){
cin >> n;
for(int i=1;i<=n-2;i++) cout << i << " " << i << "\n";
cout << n-1 << " " << n << "\n" << n << " " << n << "\n";
}补ATC abc352 D atc传送门

不知道为什么每次abc的D补着都觉得不难,但赛时就是出不了
思路:p[ i ]储存 i这个数的下标, 一个长度为 k滑动窗口不断求区间内最小值和最大值之差即可, multiset实现
代码如下:
ll n;
void solve(){
int k; cin >> n >> k;
vector<int>p(n+1);
for(int i=1;i<=n;i++){
int x; cin >> x;
p[x]=i;
}
int ans=1e9;
multiset<int>mt;
for(int i=1;i<k;i++) mt.insert(p[i]);
for(int i=k;i<=n;i++){
mt.insert(p[i]);
if(i>k) mt.erase(p[i-k]);
ans=min(*prev(mt.end())-*mt.begin(),ans);
}
cout << ans;
}星期四:
补23广东 B cf传送门

B - 基站建设 - SUA Wiki
思路:双指针预处理,然后用优先队列优化dp,dp【i】表示考虑到 i点且 i点建了基站的最小花费
优先队列优化不难,问题是怎么预处理出需要的信息,p【i】表示 [ p【i】,i ]间没有完整区间,因为p【i】满足单调不递减,可以用双指针求出
对于点 i来说,他能转移的点需要满足此条件,即下标需 >=p【i-1】-1(p【i-1】-1到 i-1 是一段区间所以p【i-1】-1 到 i-1 至少要建一个点
代码如下:
const int N=2e6+10,M=210;
const ll INF=0x3f3f3f3f3f3f3f3f;
const int mod=1e9+7;
ll n;
ll a[N];
int p[N];
vector<int>e[N];
ll dp[N];
void solve(){
cin >> n;
for(int i=1;i<=n;i++) cin >> a[i],e[i].clear();
a[++n]=0; //使n+1且a[n+1]=0,答案就能直接取dp[n]
int m; cin >> m;
while(m--){
int l,r; cin >> l >> r;
e[l].push_back(r);
e[r].push_back(-1*l);
}
for(int i=1,j=1,cnt=0;i<=n;i++){
for(int x:e[i]) if(x<0 && -1*x>=j) cnt++; //i经过右端点且其左端点>=j,则j-i的区间数+1
while(cnt>0 && j<=i){
for(int x:e[j]) if(x>0 && x<=i) cnt--; //j经过左端点且其右端点<=i,则区间数-1
j++;
}
p[i]=j;
}
priority_queue<PII,vector<PII>,greater<PII>>pq;
dp[1]=a[1],dp[0]=0;
pq.push({dp[1],1}),pq.push({dp[0],0});
for(int i=2;i<=n;i++){
while(pq.top().second<p[i-1]-1) pq.pop();
dp[i]=pq.top().first+a[i];
pq.push({dp[i],i});
}
cout << dp[n] << "\n";
}补cf round943 F(异或,附特定值下标二分 cf传送门

思路:分析异或性质可得出分块只需考虑 k=2和k=3的分法
处理出异或前缀和, 若 k==2, 则存在一点 x ,分为[ l,x ]和[ x+1,r ] 即 b[x]^b[l-1]==b[r]^b[x], 只需判断 b[l-1]是否等于 b[r]即可
若k==3, 则存在两点 s,t 分为[ l,s ], [ s+1,t ], [ t+1,r ]三个区间 ,即 b[l-1]^b[s]==b[s]^b[t]==b[t]^b[r] ,即b[s]==b[r]且b[t]==b[l-1] (s<t), 则可找出下标[ l,r ]内最接近 l的值为 b[r]的数的下标,和最接近 r的值为b[l-1]的数的下标, 可以预先把一个数出现的所有下标存进 vector里实现二分查找,最后判断 (s<t)
代码如下:
const int N=2e6+10,M=210;
const ll INF=0x3f3f3f3f3f3f3f3f;
const int mod=1e9+7;
ll n;
int a[N];
void solve(){
int q; cin >> n >> q;
map<int,vector<int>>p;
p[0].push_back(0); //先塞0下标,vector里不会自动排序
for(int i=1;i<=n;i++){
cin >> a[i];
a[i]^=a[i-1];
p[a[i]].push_back(i);
}
while(q--){
int l,r; cin >> l >> r;
if(a[l-1]==a[r]){cout << "Yes\n"; continue;}
int p1=*lower_bound(p[a[r]].begin(),p[a[r]].end(),l);
int p2=*--lower_bound(p[a[l-1]].begin(),p[a[l-1]].end(),r);
if(p1<p2) cout << "Yes\n";
else cout << "No\n";
}
cout << "\n";
}星期五:晚上vp 19年陕西省赛,坐了一晚上牢,晕晕
星期六:
补23广东 E 字典树 cf传送门

思路:新的字典树题,sum【i】表示以 i 为根的子树上有多少个字符串。字典树以1为根,后面的一些操作会更方便
在字典树上贪心地搜索答案,首先假设现在在根节点1上,lcp为空,那所有子节点上只能选择一个字符串,然后判断数量是否满足 >=k,若满足则结束搜索
若不满足,则需选择更多的字符串,从 a 到 z遍历子节点,判断答案下一位是否能为此字母,需满足 sum[ ch[ now ][ i ]] + 字典序<=该串的所有字符串数量 + 字典序>该串的子节点各选一个 >= k
代码如下:
const int N=2e6+10,M=210;
const int mod=1e9+7;
ll n;
int k;
int ch[N][30],idx,cnt[N];
ll sum[N];
void add(string s){
int p=1;
sum[p]++;
for(int i=0,sz=s.size();i<sz;i++){
int c=s[i]-'a'+1;
if(!ch[p][c]) ch[p][c]=++idx;
p=ch[p][c];
sum[p]++;
}
cnt[p]++;
}
void clr(){ //清空字典树
for(int i=0;i<=idx;i++){
for(int j=1;j<=26;j++) ch[i][j]=0;
cnt[i]=sum[i]=0;
}
}
void solve(){
cin >> n >> k;
idx=1;
for(int i=1;i<=n;i++){
string s; cin >> s;
add(s);
}
int now=1; //表示当前节点
while(1){
//判断以now结尾能选的字符串数够不够
int t=cnt[now];
for(int i=1;i<=26;i++) if(sum[ch[now][i]]) t++; //子节点的字符串只能选一个
if(t>=k){
if(now==1) cout << "EMPTY";
cout << "\n"; clr();
return ;
}
//判断接下来now该去哪个节点
for(int i=1;i<=26;i++) if(sum[ch[now][i]]){
t+=sum[ch[now][i]],t--; //判断加上ch[now][i]里所有字符串够不够
if(t>=k){ //如果够就进入该子节点
cout << char('a'+i-1);
now=ch[now][i];
k=k-t+sum[ch[now][i]]; //k减去t但要先还回sum[ch[now][i]]
break;
}
}
}
}补 19陕西 B cf传送门

题意:一言以蔽之,欧拉图
思路:欧拉图的做法,从入度的角度入手
若整个图不是一条循环的线,则起点入度为0,那么找一个入度为0的点模拟即可
若整个图就是一个循环,则所有点都可以是起点,从1,1开始模拟即可
然后判断是否所有点都被遍历
代码如下:
ll n;
int m;
vector<vector<int>>ve;
vector<vector<char>>ch;
vector<vector<bool>>vi;
vector<vector<bool>>in;
bool checkout(int x,int y){
int dis=ve[x][y];
if(ch[x][y]=='u' && x-dis<1) return 1;
if(ch[x][y]=='d' && x+dis>n) return 1;
if(ch[x][y]=='l' && y-dis<1) return 1;
if(ch[x][y]=='r' && y+dis>m) return 1;
return 0;
}
void dfs(int x,int y){
vi[x][y]=1;
if(checkout(x,y)) return ;
int dis=ve[x][y];
if(ch[x][y]=='u' && !vi[x-dis][y]) dfs(x-dis,y);
if(ch[x][y]=='d' && !vi[x+dis][y]) dfs(x+dis,y);
if(ch[x][y]=='l' && !vi[x][y-dis]) dfs(x,y-dis);
if(ch[x][y]=='r' && !vi[x][y+dis]) dfs(x,y+dis);
}
void solve(){
cin >> n >> m;
ve=vector<vector<int>>(n+10,vector<int>(m+10));
ch=vector<vector<char>>(n+10,vector<char>(m+10));
vi=vector<vector<bool>>(n+10,vector<bool>(m+10,0));
in=vector<vector<bool>>(n+10,vector<bool>(m+10,0));
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++) cin >> ch[i][j];
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin >> ve[i][j];
if(checkout(i,j)) continue;
int dis=ve[i][j];
if(ch[i][j]=='u') in[i-dis][j]=1;
if(ch[i][j]=='d') in[i+dis][j]=1;
if(ch[i][j]=='l') in[i][j-dis]=1;
if(ch[i][j]=='r') in[i][j+dis]=1;
}
}
bool if1=0;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++)
if(!in[i][j]){dfs(i,j),if1=1; break;}
if(if1) break;
}
if(!if1) dfs(1,1);
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++)
if(!vi[i][j]){cout << "No\n"; return ;}
}
cout << "Yes\n";
}周日:
补19陕西 J 位运算贪心 cf传送门

题意:给n个区间,每个区间中选一个数,使得所有数按位与的结果最大,输出最大结果
思路:按位贪心,从高到低,对于第 i位,检查所有区间是否都存在数在此位为1,若都存在则对所有区间进行缩小操作( 也可能不变,若不存在则continue
对于如何判断一区间含有第 i位为1的数,使用位运算实现,若l【i】第 i位为 1直接返回真,否则使 l【i】第 i位为1,更低位全变为0,判断其是否小于等于 r【i】
代码如下:
const int N=2e6+10,M=210;
const int mod=1e9+7;
ll n;
ll l[N],r[N];
int fnd(int x,int i){
if(!(x>>i&1)) x=((x>>i)|1)<<i; //第i位或上1,低位全变为0
return x;
}
void solve(){
cin >> n;
for(int i=1;i<=n;i++) cin >> l[i] >> r[i];
ll ans=0;
for(int i=30;i>=0;i--){
bool if1=1;
for(int j=1;j<=n;j++){
if(l[j]>>i&1) continue;
int nl=fnd(l[j],i);
if(nl>r[j]){if1=0; break;}
}
if(!if1) continue;
ans+=1ll<<i;
for(int j=1;j<=n;j++){
if(l[j]>>i&1) continue;
l[j]=fnd(l[j],i);
}
}
cout << ans << "\n";
}补ABC 353 D atc传送门
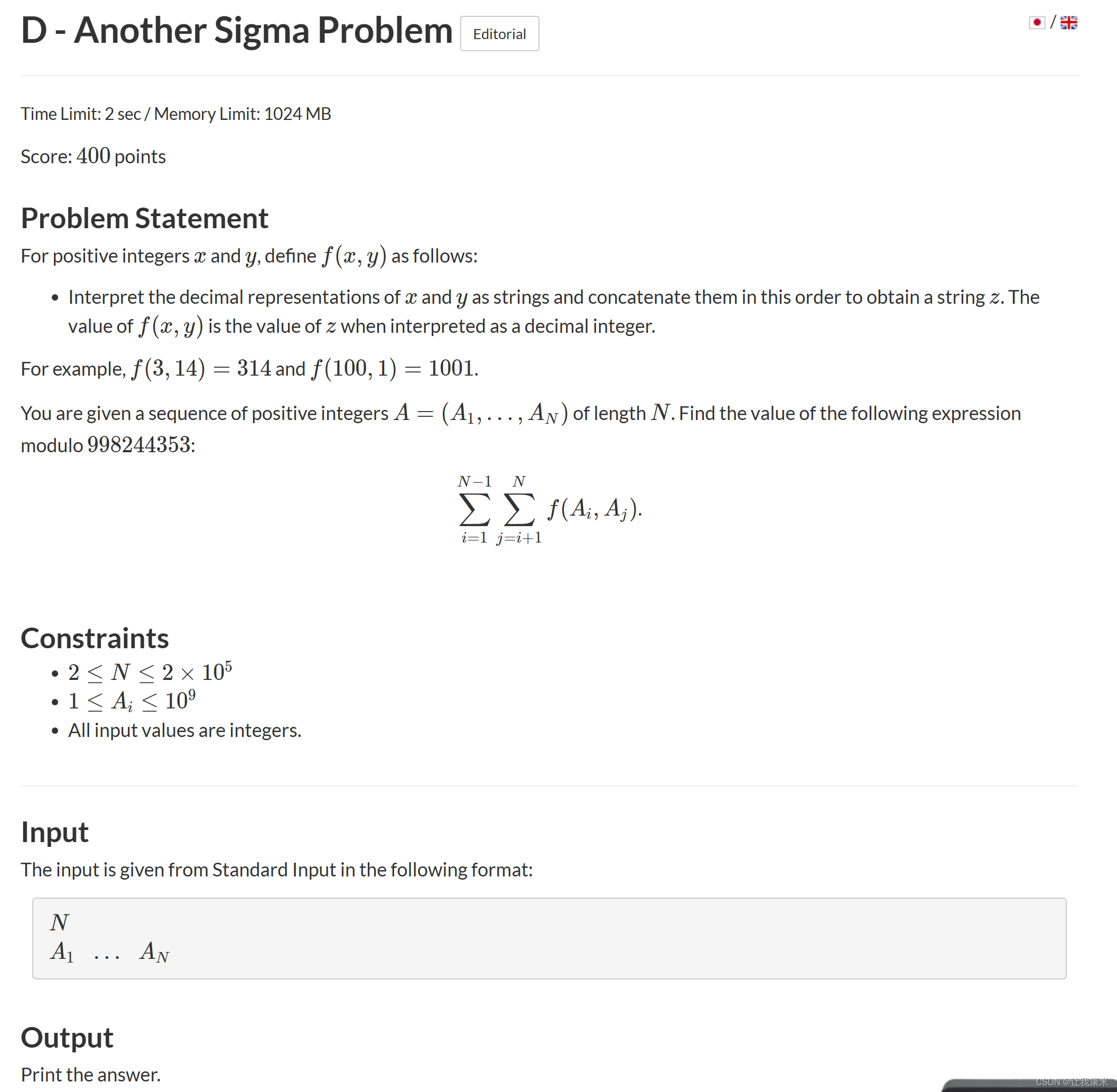
日常卡D然后补题又觉得不难
思路:做一个位数的前缀和,就能计算出一个数作为前缀的总贡献
代码如下:
const int N=2e6+10,M=210;
const int mod=998244353;
ll n;
int a[N];
int sum[N][11];
ll qpow(int a,int n){
if(n==0) return 1;
if(n==1) return a;
ll s=qpow(a,n/2);
s=s*s%mod;
if(n&1) s=s*a%mod;
return s;
}
void solve(){
cin >> n;
for(int i=1;i<=n;i++){
cin >> a[i];
string s=to_string(a[i]);
for(int j=1;j<11;j++) sum[i][j]=sum[i-1][j];
sum[i][s.size()]++;
}
ll ans=0;
for(int i=1;i<=n;i++){
for(int j=1;j<11;j++)
ans+=(1ll*a[i]*qpow(10,j)%mod)*(sum[n][j]-sum[i][j])%mod;//前缀贡献
ans+=1ll*a[i]*(i-1),ans%=mod; //后缀贡献可直接算出
}
cout << ans;
}