2.2 折半查找

• 算法思想

  • 定义：

    折半查找，又称二分查找，仅用于有序的顺序表。

  • 实现思路：

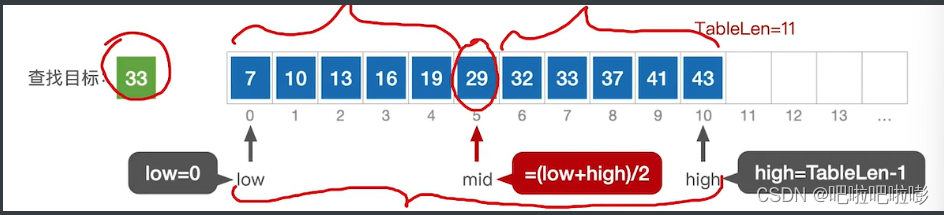
    1.设置low和high指针，分别在序列首尾；

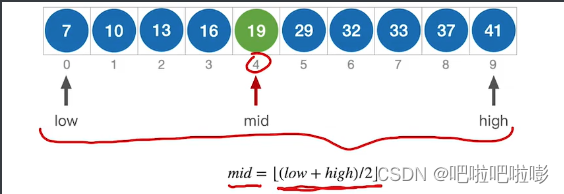
    2.取中间位置mid=(low+high)/2；

    3.若mid所指元素大，则去前半段查找，即high=mid-1；

    若mid所指元素小，则去后半段查找，即low=mid+1；

    查找成功则返回mid。

  

• 代码

  //查找表的数据结构
  typedef struct{
      ElemType *elem; //动态数组基址
      int TableLen; //表的长度
  }SSTable;
  //折半查找
  int Binary_Search(SSTable L,ElemType key){
      int low=0,high=L.TableLen-1,mid;
      while(low<=high){
          mid=(low+high)/2; //取中间位置
          if(L.elem[mid]==key)
              return mid;
          else if(L.elem[mid]>key)
              high=mid-1;
          else
              low=mid+1;
      }
      return -1;
  }
  

• 查找效率分析

  

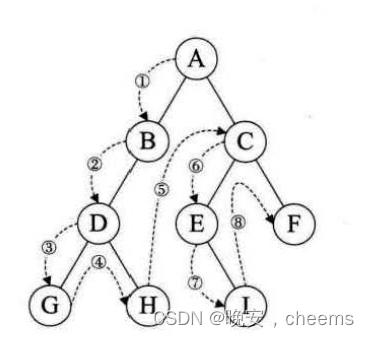
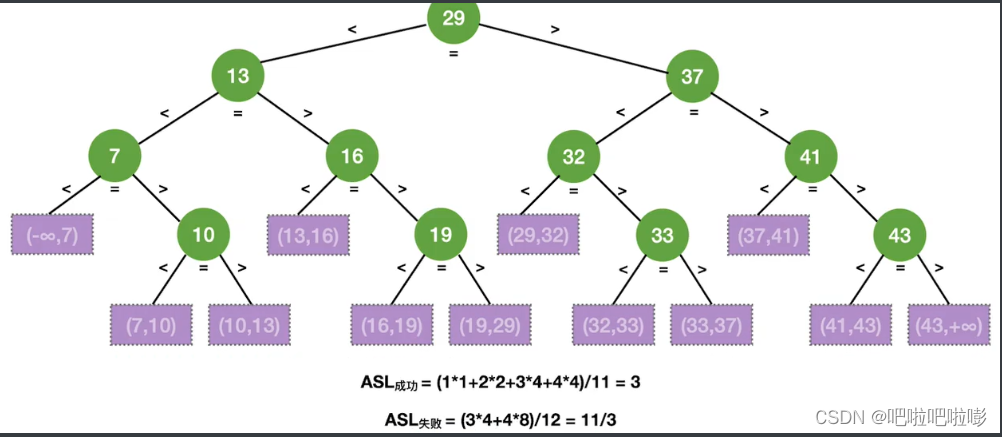
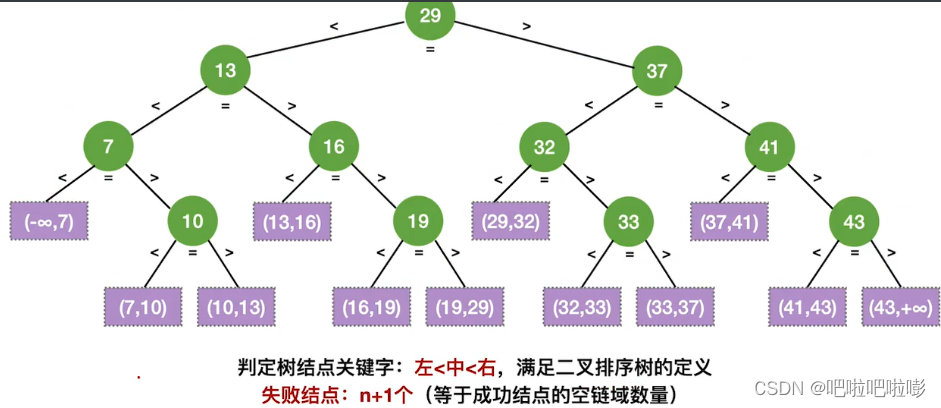
• 折半查找判定树的构造

  • 如果当前low和high之间有奇数个元素，则mid分割后，左右两部分元素个数相等。

    如果当前low和high之间有偶数个元素，则mid分割后，左半部分比右半部分少一个元素。

    

  • 折半查找的判定树一定是平衡二叉树

    折半查找的判定树中，只有最下面一层是不满的。

    因此，元素个数为n时树高$h=\lceil lo{g}_2(n+1)\rceil$

    

• 性能分析

  时间复杂度：$O(lo{g}_{2}n)$

  • 顺序查找时间复杂度为$O(n)$，但查找速度不一定是折半查找快，比如要查找第一个元素时，还是顺序查找快。

• 完整代码

  #include <stdio.h>
  #include <stdlib.h>
  
  // 定义ElemType，这里假设是int类型
  typedef int ElemType;
  
  // 定义查找表的数据结构
  typedef struct {
      ElemType *elem; // 动态数组基址
      int TableLen;   // 表的长度
  } SSTable;
  
  // 折半查找函数
  int Binary_Search(SSTable L, ElemType key) {
      int low = 0, high = L.TableLen - 1, mid;
      while (low <= high) {
          mid = (low + high) / 2; // 取中间位置
          if (L.elem[mid] == key)
              return mid;
          else if (L.elem[mid] > key)
              high = mid - 1;
          else
              low = mid + 1;
      }
      return -1;
  }
  
  int main() {
      // 初始化测试数据
      SSTable L;
      int arr[] = {1, 3, 5, 7, 9};
      L.elem = arr;
      L.TableLen = sizeof(arr) / sizeof(arr[0]);
  
      // 测试折半查找
      ElemType key = 7;
      int result = Binary_Search(L, key);
      if (result != -1) {
          printf("The element %d is found at index: %d\n", key, result);
      } else {
          printf("The element %d is not in the table\n", key);
      }
  
      return 0;
  }