前言

本文来自西湖大学赵世钰老师的B站视频。
本节课介绍最优策略和贝尔曼最优公式。贝尔曼最优公式是贝尔曼公式的一个特殊情况，本次学习有两个重要概念和一个工具。
(1) 两个概念：optimal state value 和optimal policy.
(2) 一个工具：bellman optimality equation(BOE).
强化学习的目标就是寻找最优策略，因此本文主要讲最优策略。本文大纲如下：

1、Motivating examples

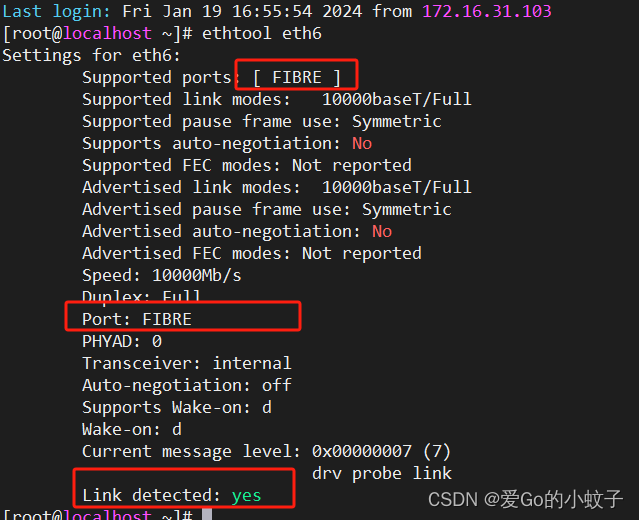
这是上节课介绍的贝尔曼方程，有了贝尔曼方程，我们就可以求解state value，有了state value，我们就可以进一步求解action value。下图是求解action value的流程，以状态s1出发为例：

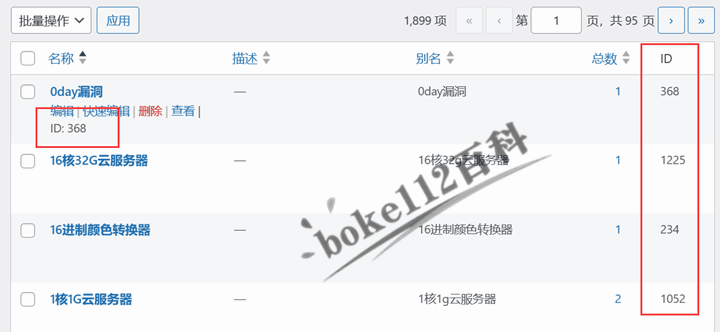
以上是对前几次课的复习，由此我们可以提出一个问题，就是当前这个策略如果是不好的，我们应该怎么去提升它？这个就依赖于action value。当前的策略可以写成以下形式：


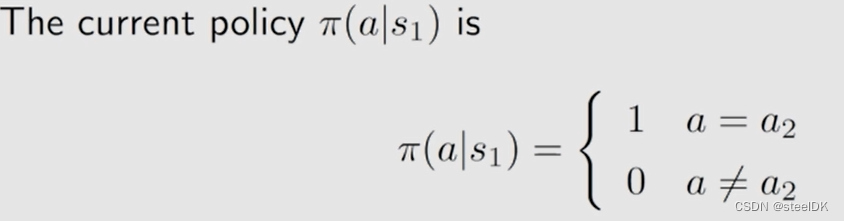
由上可知，我们已经知道a3是最好的，如果选择a3是这个新的策略，我们就获得了new policy。新的策略就是对应action value 最大。
我们首先对每一个状态都选择action value最大的 action，选择完了一次，然后再来一次迭代得到了一个新的策略，就这样不断迭代，最后那个策略就会趋向于一个最优的策略。

2、Definition of optimal policy

3、Bellman optimality equation(BOE)：Introduction

贝尔曼最优公式就是在贝尔曼公式的前面加一个max，这个max就涉及到一个优化问题，就是要先解决优化问题，求解出一个策略π，带入到贝尔曼公式中。

上面是矩阵形式。

4、 BOE：Maximization on the right-hand side

下面是BOE的两种表示形式，实际上我们是得到一个式子，但有两个未知量，如何求解呢？

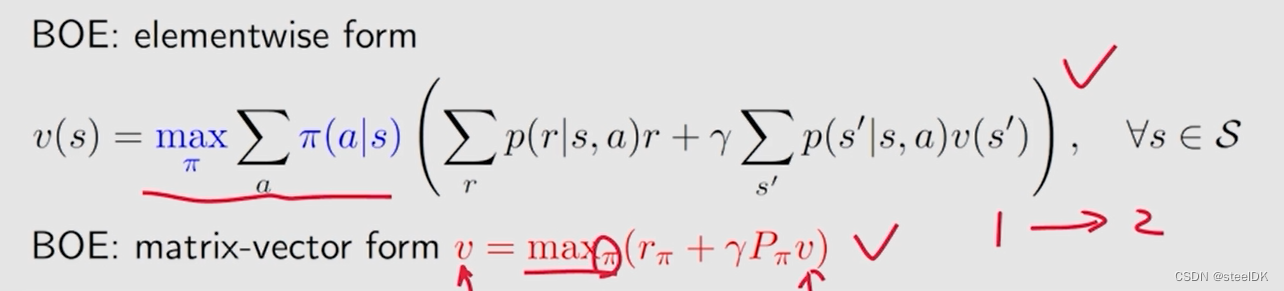
下面是一个小例子：

这个小例子的求解思路就可以放到贝尔曼最优公式求解中。

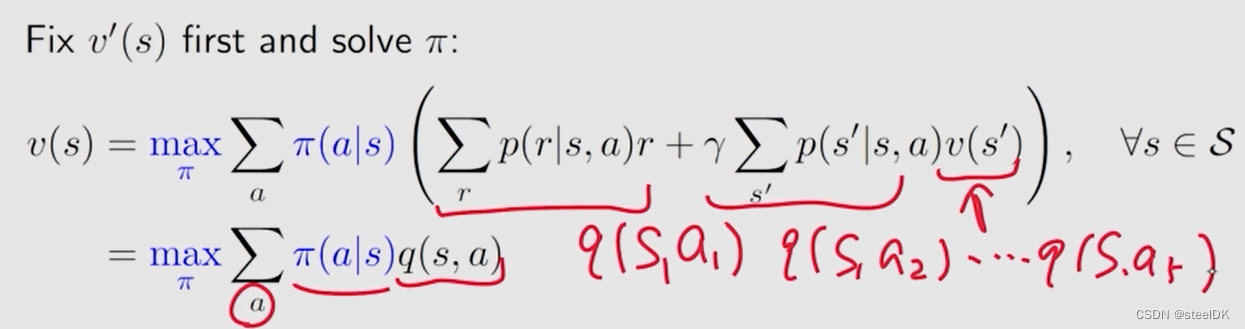
我们先给定公式右边的v(s’)一个初值，这样q(s,a)就是确定的了，此时我们需要把π(a|s)确定下来。我们知道对于网格问题有5个action，则有5个q(s，a)，我们怎样求解π(a|s)？再看一个例子，假设有3个q值：


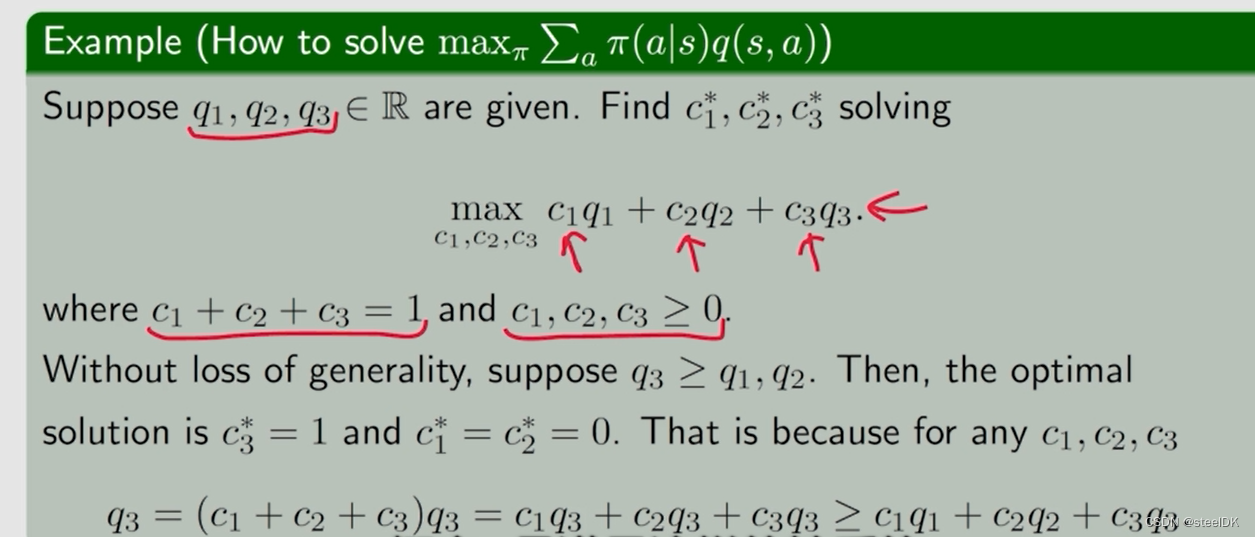
至此，我们解决了π(a|s)如何求解的问题。

5、BOE：Rewrite as v = f(v)

本文第4小节，我们知道了如何选择π(a|s)，此时贝尔曼最优公式的求解问题就变的比较简单了，我们就可以给等式右边一个初值，用矩阵迭代求解了。

6、Contraction mapping theorem

下面介绍一些概念：



以上实际上是迭代法求解矩阵收敛性的公式证明。

7、BOE：Solution

8、BOE：Optimality

9、Analyzing optimal policies

利用贝尔曼最优公式我们求解最优的策略，求解最优的state value。下面我们就用这个工具分析一些最优的策略。

已知红色的量，把黑色的量求解出来。


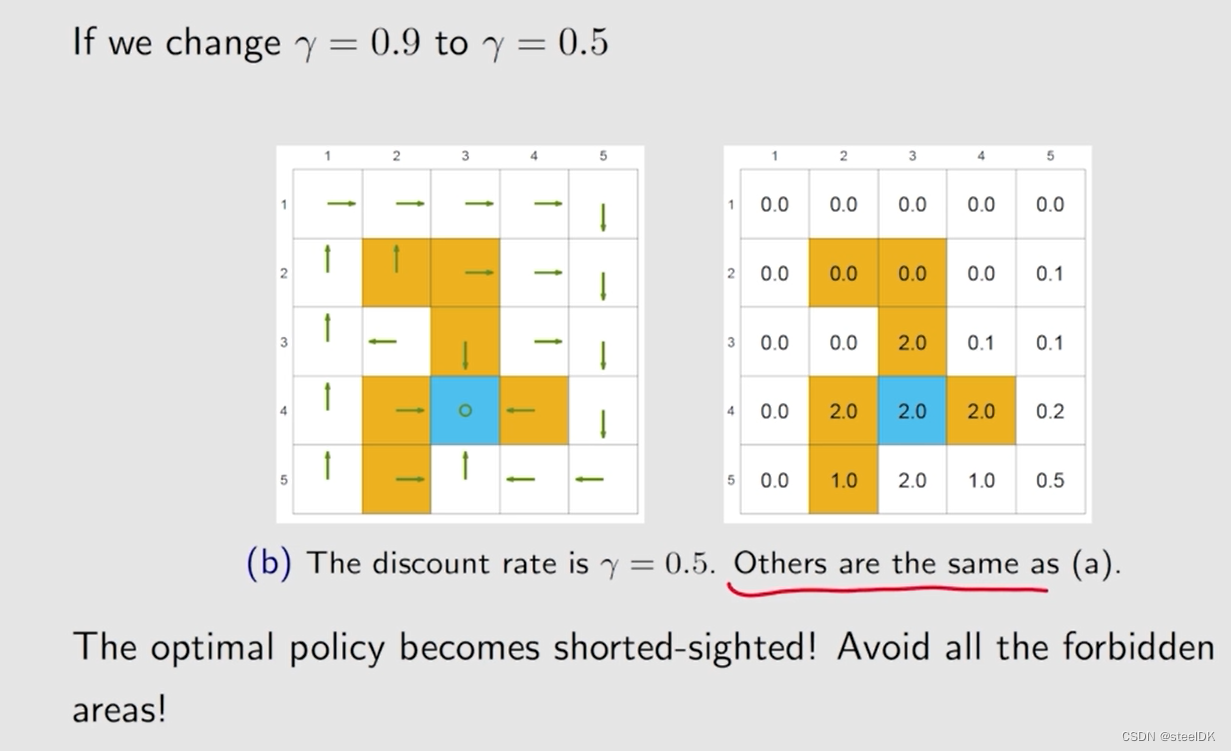
γ比较大的时候，策略会考虑的更长远。相反，γ如果等于0，策略会更加短视。

当我们把forbidden arera的惩罚值设置的比较大时，策略会选择绕过forbidden area。

策略选择的重点不在于奖励值设置的绝对大小，而在于相对大小。

下面再看一个例子：

很多人可能会觉得，我每走一步，应该给一个惩罚，即r=-1，实际当中这个r=-1就代表一种能量的消耗，这样的话智能体就不会绕远路，它就会尽可能地走最短的路径到目标区域，如果没有r=-1的话，好像就会绕远路，是这个样子吗？通过上图示例我们可以发现并不是这样子的，因为除了r来约束它不要绕远路之外，还有γ，因为它越绕远路就意味着我得到到达目标的奖励越晚，那么对应γ的次方就会越大，那么打折就会越厉害，所以它自然就会找一个最短的路径过去。

最后总结如下：