1. 概述

在CTR预估任务中，对模型特征的探索是一个重要的分支方向，尤其是特征的交叉，从早起的线性模型Logistic Regression开始，研究者在其中加入了人工的交叉特征，对最终的预估效果起到了正向的效果，但是人工的方式毕竟需要大量的人力，能否自动挖掘出特征的交叉成了研究的重要方向，随着Factorization Machines[1]的提出，模型能够自动处理二阶的特征交叉，极大减轻了人工交叉的工作量。

但是在FM中，每一个交叉特征的权重是一致的，但是在实际的工作中，不同的交叉特征应该具备不同的权重，尤其是较少使用到的权重，对于统一的权重会影响到模型的最终效果。AFM（Attentional Factorization Machines）[2]模型在FM模型的基础上，引入了Attention机制，通过Attention的网络对FM模型中的交叉特征赋予不同的权重。

2. 算法原理

2.1. FM模型中的交叉特征

FM模型中包含了两个部分，一部分是线性部分，另一部分是二阶的交叉部分，其表达式如下所示：

$$\begin{array}{cccc}{\hat{y}}_{FM}\left(\mathbf{x}\right)=& \underbrace{w_0+\sum _{i=1}^n{w}_i{x}_i}& +& \underbrace{\sum _{i=1}^n\sum _{j=i+1}^n{\hat{w}}_{ij}{x}_i{x}_j}\\ & \text{linearregression}& & \text{pair-wisefeature omteractions}\end{array}$$
其中，${\hat{w}}_{ij}$表示的是交叉特征$x_i{x}_j$的权重，在FM算法中，为了方便计算，为每一个特征赋予了一个$k$维的向量：${\mathbf{v}}_i\in {\mathbb{R}}^k$，则${\hat{w}}_{ij}$可以表示为：

$${\hat{w}}_{ij}={\mathbf{v}}_i^T{\mathbf{v}}_j$$

对于具体为甚么上述的这样的计算方式可以方便计算，可以参见参考[3]。既然上面说${\hat{w}}_{ij}$表示的是交叉特征$x_i{x}_j$的权重，那么为什么还说在FM模型中的每个交叉特征的权重是一致的，这个怎么理解？如果将FM模型放入到神经网络的框架下，FM模型的结构可以由下图表示：

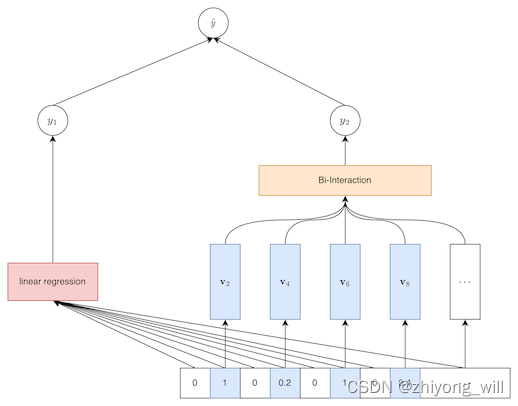
对于每一个特征都赋予一个$k$维的向量，如上图中的第二个特征$x_2$的$k$维向量为${\mathbf{v}}_2$，同理，第四个特征$x_4$的$k$维向量为${\mathbf{v}}_4$，这里类似于对原始特征的Embedding，最终$x_2$和$x_4$的交叉特征可以表示为：$\left({\mathbf{v}}_2\odot {\mathbf{v}}_4\right)x_2{x}_4$，其中，$\odot$表示的是元素的乘积。最终，将所有的交叉特征相加便得到了交叉部分$y_2$：

$$y_2={\mathbf{p}}^T\sum _{\left(i,j\right)\in {\mathfrak{R}}_x}\left({\mathbf{v}}_i\odot {\mathbf{v}}_i\right)x_i{x}_j+b$$

其中， R x = { ( i , j ) } i ∈ χ , j ∈ χ , j > i \mathfrak{R}_x=\left\{\left ( i,j \right ) \right\}_{i\in \chi ,j\in \chi,j>i} Rx​={(i,j)}i∈χ,j∈χ,j>i​，$\mathbf{p}\in {\mathbb{R}}^k$，$b\in \mathbb{R}$，在上述的FM中，$\mathbf{p}=1$，$b=0$。在相加的过程中，对于每一部分的交叉特征的权重都是一致的，这就会导致上面说的统一的权重会影响到模型的最终效果。我们希望对于每一部分的交叉特征能够有不同的权重，即：

$$y_2={\mathbf{p}}^T\sum _{\left(i,j\right)\in {\mathfrak{R}}_x}{a}_{i,j}\left({\mathbf{v}}_i\odot {\mathbf{v}}_i\right)x_i{x}_j+b$$

其中，$a_{i,j}$表示的是第$i$，$j$交叉特征部分的权重。

2.2. AFM的网络结构

在注意力FM模型AFM（Attentional Factorization Machines）中，是在FM的基础上引入了Attention机制，通过Attention网络学习到每个交叉特征的权重$a_{i,j}$，AFM的网络结构如下图所示：

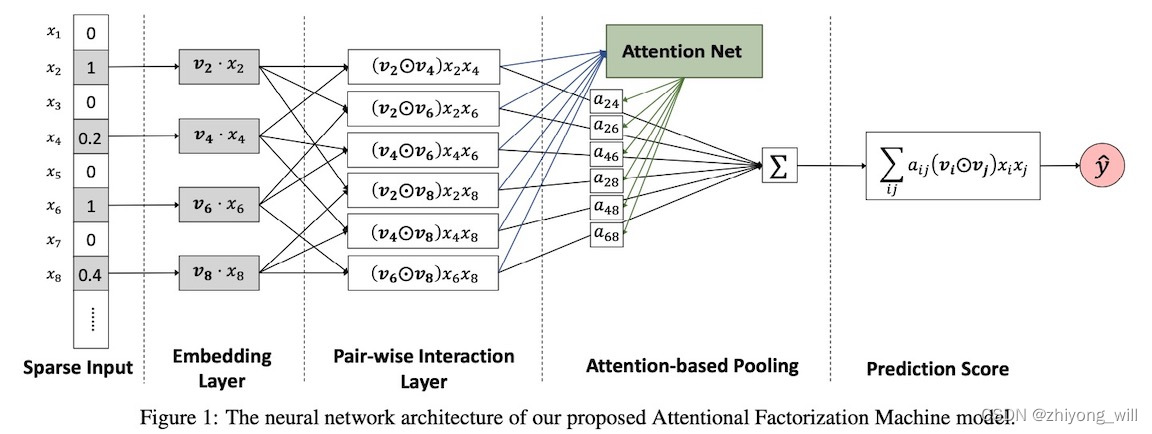
上述在Pair-wise Interaction Layer和Prediction Score之间的SUM Pooling上增加了Attention的网络，具体的数学表达式如下所示：

$${\hat{y}}_{AFM}\left(\mathbf{x}\right)=w_0+\sum _{i=1}^n{w}_i{x}_i+{\mathbf{p}}^T\sum _{i=1}^n\sum _{j=i+1}^n{a}_{ij}\left({\mathbf{v}}_i\odot {\mathbf{v}}_j\right)x_i{x}_j$$

2.3. Attention网络

对于Attention网络部分，需要计算出对于不同的交叉特征部分的权重$a_{ij}$，其中，网络的输入为$\left({\mathbf{v}}_i\odot {\mathbf{v}}_j\right)x_i{x}_j$，$a_{ij}$的计算过程如下：

$$\begin{array}{c}{a}_{ij}^{{}^{\prime }}={\mathbf{h}}^{T}ReLU\left(\mathbf{W}\left({\mathbf{v}}_i\odot {\mathbf{v}}_j\right)x_i{x}_j+\mathbf{b}\right)\\ a_{ij}=\frac{exp\left(a_{ij}^{{}^{\prime }}\right)}{{\sum }_{\left(i,j\right)\in {\mathfrak{R}}_x}exp\left(a_{ij}^{{}^{\prime }}\right)}\end{array}$$

参考[4]中给出了具体的AFM的实现，下面是Attention网络的具体实现方法：

def call(self, inputs, training=None, **kwargs):
	if K.ndim(inputs[0]) != 3:
		raise ValueError(
			"Unexpected inputs dimensions %d, expect to be 3 dimensions" % (K.ndim(inputs)))

	embeds_vec_list = inputs # 交叉特征部分
	row = []
	col = []

	for r, c in itertools.combinations(embeds_vec_list, 2):
		row.append(r)
		col.append(c)

	p = tf.concat(row, axis=1)
	q = tf.concat(col, axis=1)
	inner_product = p * q

	bi_interaction = inner_product
	attention_temp = tf.nn.relu(tf.nn.bias_add(tf.tensordot(
		bi_interaction, self.attention_W, axes=(-1, 0)), self.attention_b)) # 计算网络输出，上述公式的第一部分
	#  Dense(self.attention_factor,'relu',kernel_regularizer=l2(self.l2_reg_w))(bi_interaction)
	self.normalized_att_score = softmax(tf.tensordot(
		attention_temp, self.projection_h, axes=(-1, 0)), dim=1) # 归一化，上述公式的第二部分
	attention_output = reduce_sum(
		self.normalized_att_score * bi_interaction, axis=1) # 加权求和

	attention_output = self.dropout(attention_output, training=training)  # training，防止过拟合

	afm_out = self.tensordot([attention_output, self.projection_p]) # 乘以向量，做最终的输出
	return afm_out

3. 总结

AFM模型在FM模型的基础上，引入了Attention机制，通过Attention的网络对FM模型中的交叉特征赋予不同的权重。

参考文献

[1] Rendle S. Factorization machines[C]//2010 IEEE International conference on data mining. IEEE, 2010: 995-1000.

[2] Xiao J, Ye H, He X, et al. Attentional factorization machines: Learning the weight of feature interactions via attention networks[J]. arXiv preprint arXiv:1708.04617, 2017.

[3] 简单易学的机器学习算法——因子分解机(Factorization Machine)

[4] DeepCTR