堆

堆的概念

堆：如果有一个关键码的集合K={k0,k1,k2,…,kn-1}，把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中，并满足ki<=k2i+1且ki<=k2i+2（或满足ki>=k2i+1且ki>=k2i+2），其中i=0,1,2,…，则称该集合为堆。

1. 堆序性质：在堆中，父节点的值要么大于等于（最大堆）或小于等于（最小堆）其子节点的值。这个性质是堆的核心特征。

2. 完全二叉树结构：堆通常是一棵完全二叉树，即除了最底层外，其他层的节点都是满的，而且最底层的节点都集中在最左边。这意味着在堆中插入和删除节点时，树的形状会发生变化，但始终保持完全二叉树的性质。

3. 最大堆和最小堆：堆分为最大堆和最小堆。

   • 最大堆：每个父节点的值都大于等于其子节点的值。根节点是堆中的最大值。
   • 最小堆：每个父节点的值都小于等于其子节点的值。根节点是堆中的最小值。

堆的结构 

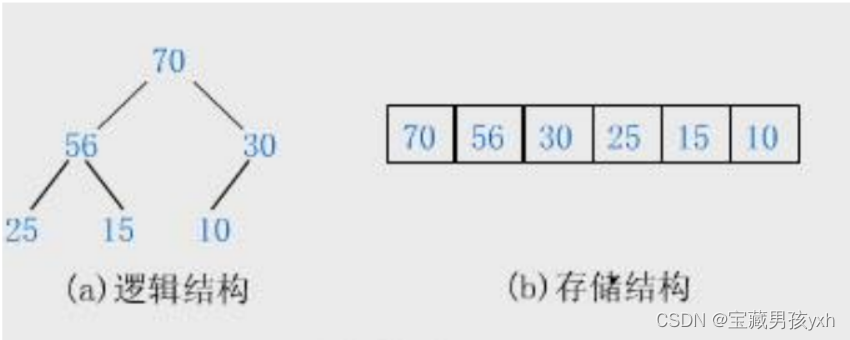
大根堆示例

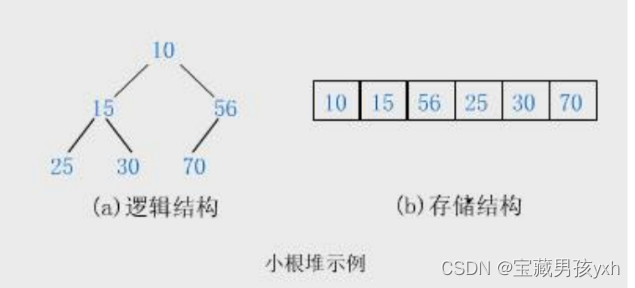
小根堆示例

堆的向下调整算法

现在我们给出一个数组，逻辑上看作一棵完全二叉树。我们通过从根节点开始的向下调整算法可以把它调整成一个小堆。

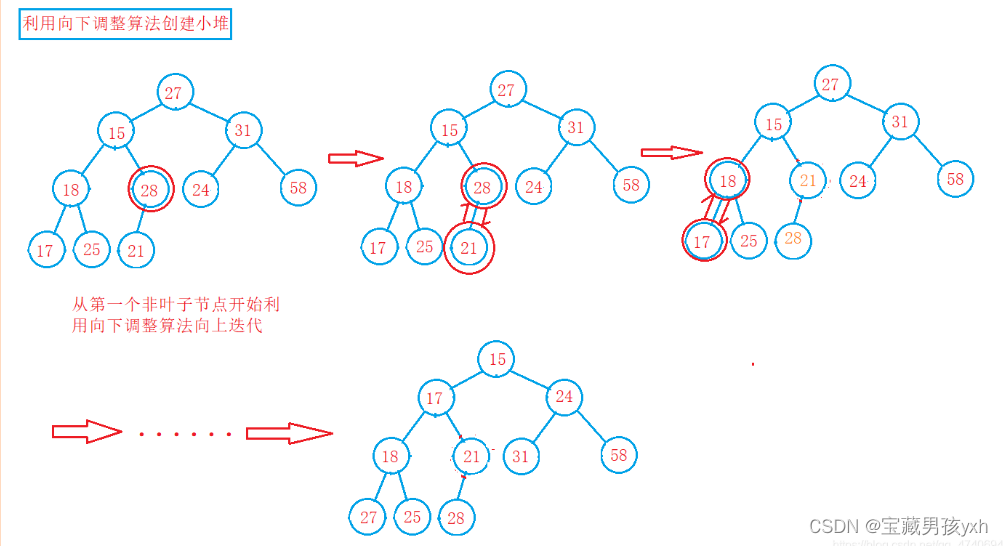
 但是，使用向下调整算法需要满足一个前提：
 若想将其调整为小堆，那么根结点的左右子树必须都为小堆。
 若想将其调整为大堆，那么根结点的左右子树必须都为大堆。

向下调整算法的基本思想（以建小堆为例）：
 1.从根结点处开始，选出左右孩子中值较小的孩子。
 2.让小的孩子与其父亲进行比较。
 若小的孩子比父亲还小，则该孩子与其父亲的位置进行交换。并将原来小的孩子的位置当成父亲继续向下进行调整，直到调整到叶子结点为止。
 若小的孩子比父亲大，则不需处理了，调整完成，整个树已经是小堆了。

代码如下：

//交换函数
void Swap(int* x, int* y)
{
	int tmp = *x;
	*x = *y;
	*y = tmp;
}

//堆的向下调整（小堆）
void AdjustDown(int* a, int n, int parent)
{
	//child记录左右孩子中值较小的孩子的下标
	int child = 2 * parent + 1;//先默认其左孩子的值较小
	while (child < n)
	{
		if (child + 1 < n&&a[child + 1] < a[child])//右孩子存在并且右孩子比左孩子还小
		{
			child++;//较小的孩子改为右孩子
		}
		if (a[child] < a[parent])//左右孩子中较小孩子的值比父结点还小
		{
			//将父结点与较小的子结点交换
			Swap(&a[child], &a[parent]);
			//继续向下进行调整
			parent = child;
			child = 2 * parent + 1;
		}
		else//已成堆
		{
			break;
		}
	}
}

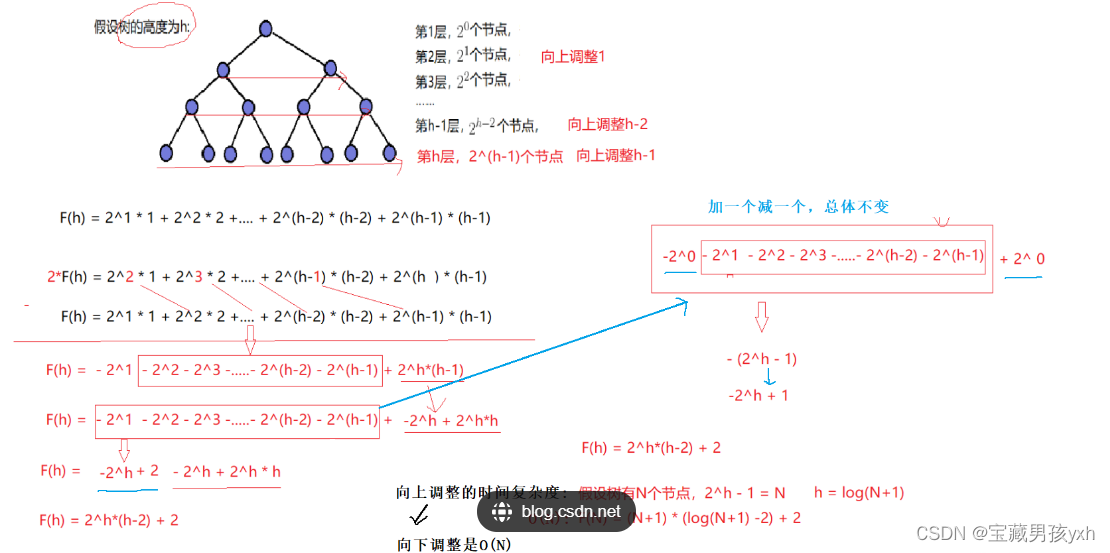
那么建堆的时间复杂度又是多少呢？
 当结点数无穷大时，完全二叉树与其层数相同的满二叉树相比较来说，它们相差的结点数可以忽略不计，所以计算时间复杂度的时候我们可以将完全二叉树看作与其层数相同的满二叉树来进行计算。

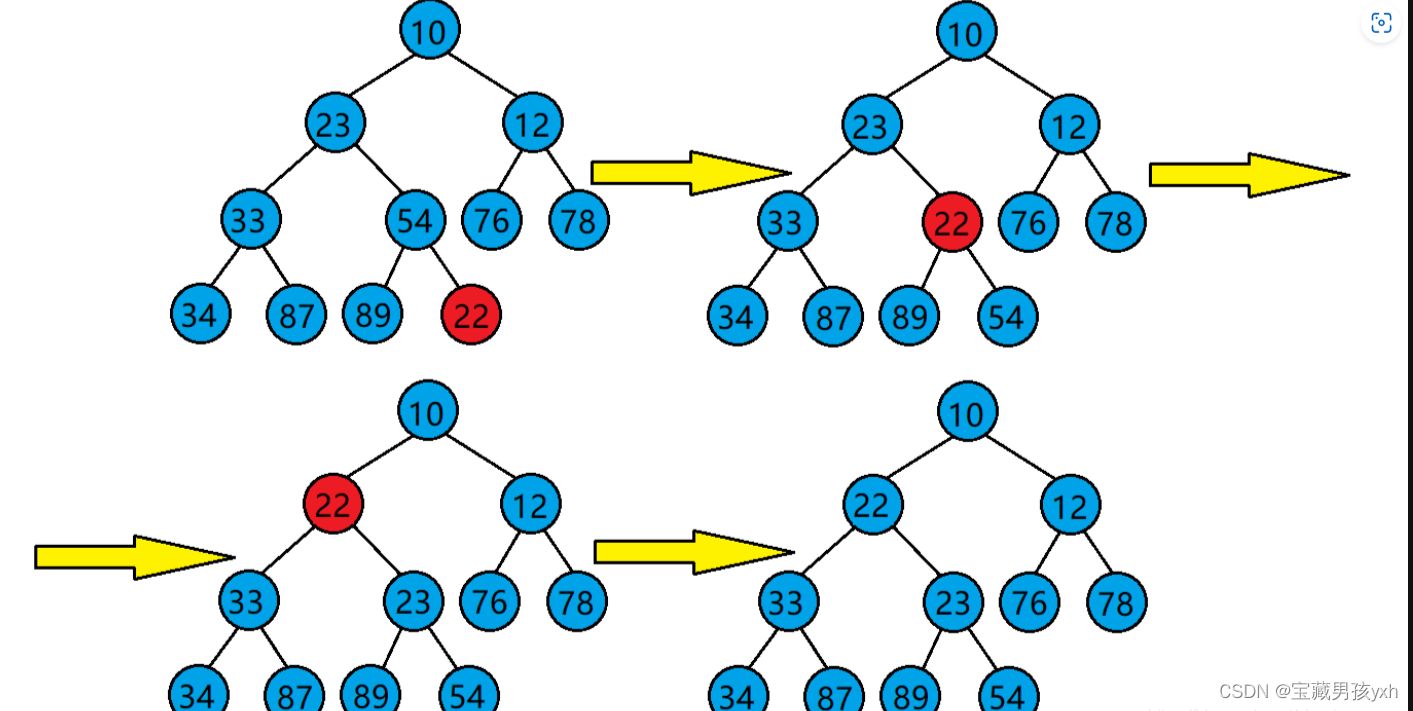
堆的向上调整算法

当我们在一个堆的末尾插入一个数据后，需要对堆进行调整，使其仍然是一个堆，这时需要用到堆的向上调整算法。 

代码实现

//交换函数
void Swap(HPDataType* x, HPDataType* y)
{
	HPDataType tmp = *x;
	*x = *y;
	*y = tmp;
}

//堆的向上调整（小堆）
void AdjustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;
	while (child > 0)//调整到根结点的位置截止
	{
		if (a[child] < a[parent])//孩子结点的值小于父结点的值
		{
			//将父结点与孩子结点交换
			Swap(&a[child], &a[parent]);
			//继续向上进行调整
			child = parent;
			parent = (child - 1) / 2;
		}
		else//已成堆
		{
			break;
		}
	}
}

 堆的实现

初始化堆

// 初始化堆
HeapNode* initializeHeap() {
    return nullptr; // 返回空指针表示空堆
}

判断堆是否为空

// 判断堆是否为空
bool isEmpty(HeapNode* heap) {
    return heap == nullptr;
}

这个函数简单地检查堆是否为空，如果堆是空的则返回true，否则返回false。

插入元素

// 向堆中插入元素
HeapNode* insertElement(HeapNode* heap, int val) {
    HeapNode* newNode = new HeapNode(val); // 创建新节点
    if (isEmpty(heap)) {
        return newNode; // 如果堆为空，新节点即为根节点
    } else {
        // 找到最后一个节点
        HeapNode* temp = heap;
        while (temp->left != nullptr && temp->right != nullptr) {
            temp = temp->left; // 堆是一个完全二叉树，所以优先插入左子节点
        }
        // 插入新节点作为最后一个节点的左子节点
        if (temp->left == nullptr) {
            temp->left = newNode;
        } else {
            temp->right = newNode;
        }
        return heap;
    }
}

这个函数首先创建一个新节点，然后判断堆是否为空。如果堆为空，新节点即为根节点。如果堆不为空，函数会找到最后一个节点，然后将新节点插入为其左子节点（优先插入左子节点）或右子节点。

删除元素

// 从堆中删除元素
HeapNode* deleteElement(HeapNode* heap, int val) {
    if (heap == nullptr) {
        std::cout << "Heap is empty." << std::endl;
        return heap; // 如果堆为空，直接返回
    }

    // 先找到要删除的节点及其父节点
    HeapNode* parent = nullptr;
    HeapNode* nodeToDelete = heap;
    while (nodeToDelete != nullptr && nodeToDelete->value != val) {
        parent = nodeToDelete;
        if (val < nodeToDelete->value) {
            nodeToDelete = nodeToDelete->left;
        } else {
            nodeToDelete = nodeToDelete->right;
        }
    }

    // 如果未找到要删除的节点
    if (nodeToDelete == nullptr) {
        std::cout << "Element not found in heap." << std::endl;
        return heap;
    }

    // 如果要删除的节点有两个子节点
    if (nodeToDelete->left != nullptr && nodeToDelete->right != nullptr) {
        // 找到要删除节点的右子树中最小的节点
        HeapNode* minRight = nodeToDelete->right;
        while (minRight->left != nullptr) {
            minRight = minRight->left;
        }
        // 用最小右节点的值替换要删除的节点的值
        nodeToDelete->value = minRight->value;
        // 删除最小右节点
        heap = deleteElement(heap, minRight->value);
        return heap;
    }

    // 如果要删除的节点是叶子节点或只有一个子节点
    if (nodeToDelete->left == nullptr) {
        if (parent != nullptr) {
            if (parent->left == nodeToDelete) {
                parent->left = nodeToDelete->right;
            } else {
                parent->right = nodeToDelete->right;
            }
        } else {
            heap = nodeToDelete->right;
        }
        delete nodeToDelete;
        return heap;
    }

    if (nodeToDelete->right == nullptr) {
        if (parent != nullptr) {
            if (parent->left == nodeToDelete) {
                parent->left = nodeToDelete->left;
            } else {
                parent->right = nodeToDelete->left;
            }
        } else {
            heap = nodeToDelete->left;
        }
        delete nodeToDelete;
        return heap;
    }

    return heap;
}

删除元素代码解释

这段代码实现了从堆中删除元素的功能。让我来解释一下：

1. 首先，我们检查堆是否为空，如果为空则输出错误信息并直接返回。

2. 接着，我们使用循环来找到要删除的节点以及其父节点。循环条件是当前节点不为空且当前节点的值不等于待删除的值，根据待删除的值和当前节点值的比较结果来决定往左子树还是右子树走。

3. 如果我们找到了要删除的节点：

   • 如果要删除的节点有两个子节点，则我们需要找到其右子树中的最小节点（即右子树中的最左下角的节点），将其值替换到待删除的节点中，然后递归地删除最小节点。

   • 如果要删除的节点是叶子节点或只有一个子节点，则我们将其子节点链接到其父节点上，并删除待删除的节点。

4. 最后，我们返回调整后的堆。

打印元素

// 打印堆中的元素
void printHeap(HeapNode* heap) {
    if (isEmpty(heap)) {
        std::cout << "Heap is empty." << std::endl;
        return;
    }
    // 使用中序遍历打印堆中的所有元素
    printHeap(heap->left);
    std::cout << heap->value << " ";
    printHeap(heap->right);
}

销毁堆

// 销毁堆
void destroyHeap(HeapNode* heap) {
    if (heap != nullptr) {
        destroyHeap(heap->left); // 递归销毁左子树
        destroyHeap(heap->right); // 递归销毁右子树
        delete heap; // 释放当前节点内存
    }
}