目录
- 引言
- 区间合并模板
- 一、石子合并
- 二、环形石子合并
- 三、能量项链
引言
关于这个区间 D P DP DP ,其实是有套路和模板的,题型的话也是变化不多,感觉就那几种,只不过有些题会用到高精度或者是要记录方案,所以整体来说还是比较容易的了,然后这种题型还是多见的为好,目前也只是会做这几道题。其实关于蓝桥杯只要你暴力都能打满,那么国三是稳了的,如果能做对大概两道题,那么就能拿国二,所以说搞这个 D P DP DP 也只是看能不能碰见做过类似的题目,现场解题我是不敢想了,太难的压根做不出来,但也不能完全不学,不是特别难的还是要学,万一出了那就是自己赚了,所以继续加油吧,另外感觉身体累了,也是要合理的休息的!
区间合并模板
memset(f, 0x3f, sizeof f); //先全部初始化为非法状态
for(int len = 1; len <= n; ++len) // 确定r
{
for(int l = 1; l + len - 1 <= n; ++l) //确定l
{
int r = l + len - 1;
if(l == r) f[l][r] = 0; // 计算f[l][r]
else // 计算f[l][r]
{
for(int k = l; k < r; ++k) f[l][r] = min(f[l][r], f[l][k] + f[k+1][r] + ...);
}
}
}
一、石子合并
标签:动态规划、区间DP
思路:这个区间
D
P
DP
DP 其实用之前的分析法也是可以的,一般状态定义都是看经验,定义一个状态
f
[
i
]
[
j
]
f[i][j]
f[i][j] 代表合并
i
∼
j
i \sim j
i∼j 区间内的石子所要花费的最小的代价,状态计算也是跟那个
F
l
o
y
d
Floyd
Floyd 算法差不多,就是把这一个区间按照倒数第二步划分,也就是把
f
[
i
]
[
j
]
f[i][j]
f[i][j] 按照分界点划分为
f
[
i
]
[
k
]
,
f
[
k
+
1
]
[
j
]
f[i][k],f[k+1][j]
f[i][k],f[k+1][j] ,然后再进行取最小值。两堆石子合并所花费的最小的代价,就是合并成两堆石子各自的最小代价加上这两堆石子总的代价,前面的也就是
f
[
i
]
[
k
]
,
f
[
k
+
1
]
[
j
]
f[i][k],f[k+1][j]
f[i][k],f[k+1][j] 了,后面的可以直接拿前缀和来做即可。那么状态转移方程就为
f
[
l
]
[
r
]
=
m
i
n
(
f
[
l
]
[
r
]
,
f
[
l
]
[
k
]
+
f
[
k
+
1
]
[
r
]
+
s
[
r
]
−
s
[
l
−
1
]
)
f[l][r] = min(f[l][r], f[l][k]+f[k+1][r] + s[r] - s[l-1])
f[l][r]=min(f[l][r],f[l][k]+f[k+1][r]+s[r]−s[l−1]) ,然后初始的状态
f
[
i
]
[
i
]
f[i][i]
f[i][i] 的值为
0
0
0 ,然后其余的都是非法的,并且该题求的是最小值,所以初始化为正无穷即可。剩余的就按照模板即可。
题目描述:
设有 N 堆石子排成一排,其编号为 1,2,3,…,N。
每堆石子有一定的质量,可以用一个整数来描述,现在要将这 N 堆石子合并成为一堆。
每次只能合并相邻的两堆,合并的代价为这两堆石子的质量之和,合并后与这两堆石子相邻的石子将和新堆相邻,合并时由于选
择的顺序不同,合并的总代价也不相同。
例如有 4 堆石子分别为 1 3 5 2, 我们可以先合并 1、2 堆,代价为 4,得到 4 5 2, 又合并 1、2 堆,代价为 9,得到 9 2 ,再合
并得到 11,总代价为 4+9+11=24;
如果第二步是先合并 2、3 堆,则代价为 7,得到 4 7,最后一次合并代价为 11,总代价为 4+7+11=22。
问题是:找出一种合理的方法,使总的代价最小,输出最小代价。
输入格式
第一行一个数 N 表示石子的堆数 N。
第二行 N 个数,表示每堆石子的质量(均不超过 1000)。
输出格式
输出一个整数,表示最小代价。
数据范围
1≤N≤300
输入样例:
4
1 3 5 2
输出样例:
22
示例代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y second
const int N = 310, M = N, INF = 0x3f3f3f3f;
int n, m;
int s[N], f[N][N];
int main()
{
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
cin >> n;
for(int i = 1; i <= n; ++i) cin >> s[i], s[i] += s[i-1];
memset(f, 0x3f, sizeof f);
for(int len = 1; len <= n; ++len)
{
for(int l = 1; l + len - 1 <= n; ++l)
{
int r = l + len - 1;
if(l == r) f[l][r] = 0;
else
{
for(int k = l; k < r; ++k) f[l][r] = min(f[l][r], f[l][k] + f[k+1][r] + s[r] - s[l-1]);
}
}
}
cout << f[1][n] << endl;
return 0;
}
二、环形石子合并
标签:DP、区间DP、环形区间DP
思路:这道题跟上一道题唯一的不同就是该题的石子是环形的,不是链形的,解决的办法都是在该链的基础上在追加一条链,然后在此基础上做区间
D
P
DP
DP ,最后再枚举每
n
n
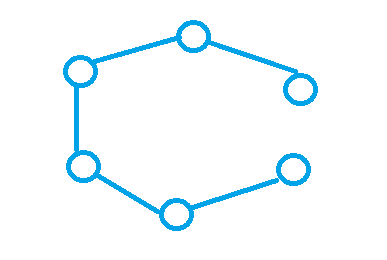
n 堆石子找最值。为什么这样做是正确的呢,如下图所示,如果我们把圆圈看作石子,连边看作是石子之间的合并,那么必然会连
n
−
1
n-1
n−1 条边,那么肯定会如下图所示会有一个缺口,我们把其展开就是一条长度为
n
n
n 的链了,那么我们直接枚举这个缺口,也就是在
2
n
2n
2n 的长度下做区间为
n
n
n 的区间合并,最后再枚举所有长度为
n
n
n 的区间的结果即可。其余的初始化等细节,详情见代码。
题目描述:
将 n 堆石子绕圆形操场排放,现要将石子有序地合并成一堆。
规定每次只能选相邻的两堆合并成新的一堆,并将新的一堆的石子数记做该次合并的得分。
请编写一个程序,读入堆数 n 及每堆的石子数,并进行如下计算:
选择一种合并石子的方案,使得做 n−1 次合并得分总和最大。选择一种合并石子的方案,使得做 n−1 次合并得分总和最小。
输入格式
第一行包含整数 n,表示共有 n 堆石子。
第二行包含 n 个整数,分别表示每堆石子的数量。
输出格式
输出共两行:
第一行为合并得分总和最小值,
第二行为合并得分总和最大值。
数据范围
1≤n≤200
输入样例:
4
4 5 9 4
输出样例:
43
54
示例代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y second
const int N = 410, M = N, INF = 0x3f3f3f3f;
int n, m;
int w[N], s[N];
int f[N][N], g[N][N];
int main()
{
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
cin >> n;
for(int i = 1; i <= n; ++i)
{
cin >> w[i];
w[i+n] = w[i];
}
for(int i = 1; i <= n * 2; ++i) s[i] = w[i] + s[i-1];
memset(f, 0x3f, sizeof f);
memset(g, -0x3f, sizeof g);
for(int len = 1; len <= n; ++len)
{
for(int l = 1; l + len - 1 <= n * 2; ++l)
{
int r = l + len - 1;
if(l == r) f[l][r] = g[l][r] = 0;
else
{
for(int k = l; k < r; ++k)
{
f[l][r] = min(f[l][r], f[l][k] + f[k+1][r] + s[r] - s[l-1]);
g[l][r] = max(g[l][r], g[l][k] + g[k+1][r] + s[r] - s[l-1]);
}
}
}
}
int r1 = INF, r2 = -INF;
for(int i = 1; i <= n; ++i)
{
r1 = min(r1, f[i][i+n-1]);
r2 = max(r2, g[i][i+n-1]);
}
cout << r1 << endl << r2 << endl;
return 0;
}
三、能量项链
标签:DP、区间DP、破环成链
思路:这道题其实跟上一道题是差不多的, 区别就是
l
e
n
len
len 最小从
2
2
2 变成
3
3
3 了,并且总的长度变为了
n
+
1
n+1
n+1 ,由于题目特性,两颗珠子根据首尾也能合并成一个珠子。所以最终的结果就是
f
[
i
]
[
i
+
n
]
f[i][i+n]
f[i][i+n] 里选一个,因为
l
e
n
len
len 最小是
3
3
3 ,所以
l
<
k
<
r
l<k<r
l<k<r ,状态转移方程为
∑
k
=
l
+
1
k
=
r
−
1
f
[
l
]
[
r
]
=
m
a
x
(
f
[
l
]
[
r
]
,
f
[
l
]
[
k
]
+
f
[
k
]
[
r
]
+
w
[
l
]
∗
w
[
k
]
∗
w
[
r
]
)
\sum_{k=l+1}^{k=r-1} f[l][r] = max(f[l][r], f[l][k] + f[k][r] + w[l] * w[k] * w[r])
∑k=l+1k=r−1f[l][r]=max(f[l][r],f[l][k]+f[k][r]+w[l]∗w[k]∗w[r]) 。其余的就是模板,细节见代码。
题目描述:
在 Mars 星球上,每个 Mars 人都随身佩带着一串能量项链,在项链上有 N 颗能量珠。
能量珠是一颗有头标记与尾标记的珠子,这些标记对应着某个正整数。
并且,对于相邻的两颗珠子,前一颗珠子的尾标记一定等于后一颗珠子的头标记。
因为只有这样,通过吸盘(吸盘是 Mars 人吸收能量的一种器官)的作用,这两颗珠子才能聚合成一颗珠子,同时释放出可以被
吸盘吸收的能量。
如果前一颗能量珠的头标记为 m,尾标记为 r,后一颗能量珠的头标记为 r,尾标记为 n,则聚合后释放的能量为 m×r×n
(Mars 单位),
新产生的珠子的头标记为 m,尾标记为 n。
需要时,Mars 人就用吸盘夹住相邻的两颗珠子,通过聚合得到能量,直到项链上只剩下一颗珠子为止。
显然,不同的聚合顺序得到的总能量是不同的,请你设计一个聚合顺序,使一串项链释放出的总能量最大。
例如:设 N=4,4 颗珠子的头标记与尾标记依次为 (2,3)(3,5)(5,10)(10,2)。
我们用记号 ⊕ 表示两颗珠子的聚合操作,(j⊕k) 表示第 j,k 两颗珠子聚合后所释放的能量。则
第 4、1 两颗珠子聚合后释放的能量为:(4⊕1)=10×2×3=60。
这一串项链可以得到最优值的一个聚合顺序所释放的总能量为 ((4⊕1)⊕2)⊕3)=10×2×3+10×3×5+10×5×10=710。
输入格式
输入的第一行是一个正整数 N,表示项链上珠子的个数。
第二行是 N 个用空格隔开的正整数,所有的数均不超过 1000,第 i 个数为第 i 颗珠子的头标记,当 i<N 时,第 i 颗珠子的尾标记
应该等于第 i+1 颗珠子的头标记,第 N 颗珠子的尾标记应该等于第 1 颗珠子的头标记。
至于珠子的顺序,你可以这样确定:将项链放到桌面上,不要出现交叉,随意指定第一颗珠子,然后按顺时针方向确定其他珠子的顺序。
输出格式
输出只有一行,是一个正整数 E,为一个最优聚合顺序所释放的总能量。
数据范围
4≤N≤100,1≤E≤2.1×109
输入样例:
4
2 3 5 10
输出样例:
710
示例代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y second
const int N = 210, M = N, INF = 0x3f3f3f3f;
int n, m;
int w[N], f[N][N];
int main()
{
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
cin >> n;
for(int i = 1; i <= n; ++i) cin >> w[i], w[i+n] = w[i];
memset(f, -0x3f, sizeof f);
for(int len = 1; len <= n + 1; ++len)
{
for(int l = 1; l + len - 1 <= n * 2; ++l)
{
int r = l + len - 1;
if(r - l + 1 < 3) f[l][r] = 0;
else
{
for(int k = l + 1; k < r; ++k)
{
f[l][r] = max(f[l][r], f[l][k] + f[k][r] + w[l] * w[k] * w[r]);
}
}
}
}
int res = 0;
for(int i = 1; i <= n; ++i)
{
res = max(res, f[i][i+n]);
}
cout << res << endl;
return 0;
}