曲线在SVG中通常是通过贝塞尔曲线命令来绘制的，包括二次贝塞尔曲线（Q）和三次贝塞尔曲线（C）。这些命令允许我们创建平滑的曲线路径。

贝塞尔曲线的原理

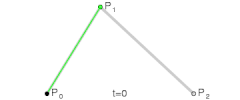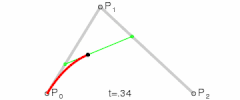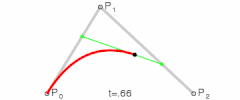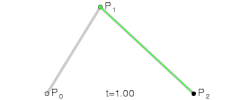
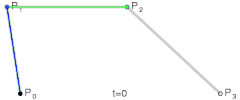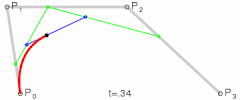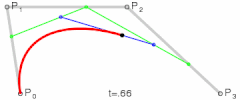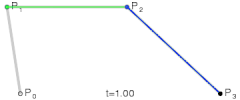
贝塞尔曲线的基本原理是通过控制点和锚点来定义一条曲线的形状。对于二次贝塞尔曲线，有一个起点、一个控制点和一个终点；而三次贝塞尔曲线则有两个控制点。控制点决定了曲线的弯曲程度和方向。

绘制过程

1. 二次贝塞尔曲线（Quadratic Bézier Curve）:
   • 使用Q命令，后跟一个控制点和一个终点坐标。
   • 控制点决定了从起点到终点的曲线弯曲的程度和方向。

1. 三次贝塞尔曲线（Cubic Bézier Curve）:
   • 使用C命令，后跟两个控制点和一个终点坐标。
   • 第一个控制点影响曲线起始部分的方向和长度，第二个控制点影响曲线结束部分的方向和长度。

绘制二次贝塞尔曲线（Q）

二次贝塞尔曲线由一个起点、一个控制点和一个终点定义。其命令格式如下：

<path d="M x1 y1 Q x2 y2 x3 y3" />

• M x1 y1 表示路径的起点。
• Q 是二次贝塞尔曲线的指令。
• x2 y2 是控制点的坐标，它决定了曲线的弯曲程度和方向。
• x3 y3 是曲线的终点。

二次贝塞尔曲线示例

<!-- SVG容器 -->
<svg width="200" height="200">
  <!-- 绘制二次贝塞尔曲线 -->
  <path d="M 10 80
           Q 95 10 180 80" 
        stroke="black" fill="transparent"/>
  <!-- 起点 -->
  <circle cx="10" cy="80" r="3" fill="red"/>
  <!-- 控制点 -->
  <circle cx="95" cy="10" r="3" fill="green"/>
  <!-- 终点 -->
  <circle cx="180" cy="80" r="3" fill="blue"/>
</svg>

• M 10 80 表示移动到起点(10,80)。
• Q 95 10 180 80 表示绘制二次贝塞尔曲线。95 10 是控制点，180 80 是终点。
• stroke="black" 设置曲线颜色为黑色。
• fill="transparent" 设置填充颜色为透明。
• <circle> 元素用来标示起点、控制点和终点。

绘制三次贝塞尔曲线（C）

三次贝塞尔曲线比二次贝塞尔曲线多了一个控制点，因此提供了更高的控制精度。其命令格式如下：

<path d="M x1 y1 C x2 y2 x3 y3 x4 y4" />

• M x1 y1 表示路径的起点。
• C 是三次贝塞尔曲线的指令。
• x2 y2 和 x3 y3 是控制点的坐标，它们共同决定了曲线的形状。
• x4 y4 是曲线的终点。

三次贝塞尔曲线示例

<!-- SVG容器 -->
<svg width="200" height="200">
  <!-- 绘制三次贝塞尔曲线 -->
  <path d="M 10 150
           C 40 10, 150 10, 180 150" 
        stroke="black" fill="transparent"/>
  <!-- 起点 -->
  <circle cx="10" cy="150" r="3" fill="red"/>
  <!-- 第一个控制点 -->
  <circle cx="40" cy="10" r="3" fill="green"/>
  <!-- 第二个控制点 -->
  <circle cx="150" cy="10" r="3" fill="green"/>
  <!-- 终点 -->
  <circle cx="180" cy="150" r="3" fill="blue"/>
</svg>

• M 10 150 表示移动到起点(10,150)。
• C 40 10, 150 10, 180 150 表示绘制三次贝塞尔曲线。40 10 和 150 10 是控制点，180 150 是终点。
• stroke="black" 和 fill="transparent" 的设置与二次贝塞尔曲线相同。
• <circle> 元素同样用来标示起点、控制点和终点。

以上代码中，红色的圆点表示起点，绿色的圆点表示控制点，蓝色的圆点表示终点。通过调整控制点的位置，可以改变曲线的形状

示例：绘制一个心形

下面是一个使用三次贝塞尔曲线绘制心形的示例：

<svg width="100" height="100">
  <path d="M 10 30
           C 10 10, 30 10, 30 30
           C 30 50, 10 50, 10 30
           Z" fill="red"/>
</svg>

在这个例子中，我们使用了两个C命令来绘制心形的上半部分，然后用Z命令闭合路径。

通过调整控制点的位置，你可以改变曲线的形状。实践中，你可能需要多次尝试来找到合适的控制点位置，以便绘制出理想的曲线形状。