题目链接

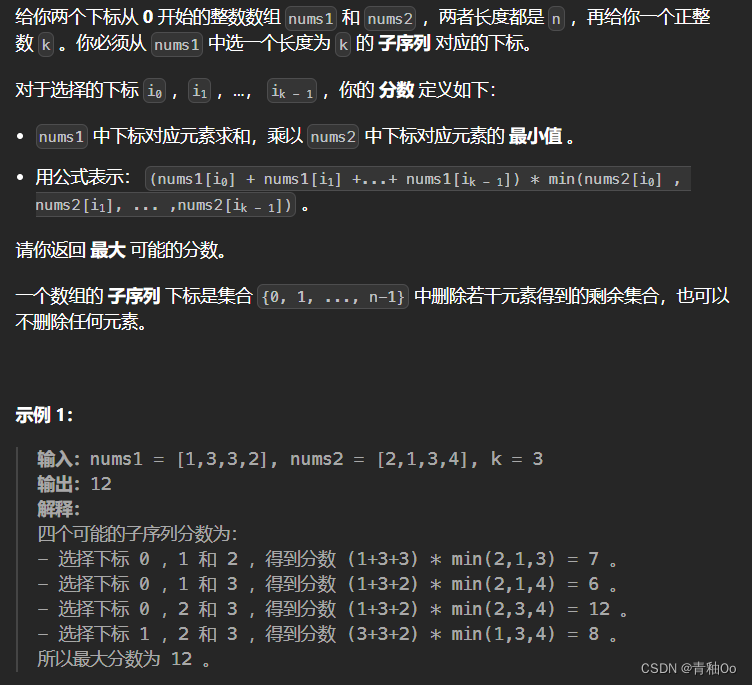
最大子序列的分数

题目描述

注意点

• n == nums1.length == nums2.length
• 从nums1和nums2中选一个长度为k的子序列对应的下标
• 对nums1中下标对应元素求和，乘以nums2中下标对应元素的最小值得到子序列的分数
• 0 <= nums1[i], nums2[j] <= 100000
• 1 <= k <= n

解答思路

• 初始想到的是深度优先遍历，传递nums1子序列的和以及nums2中值最小的元素，当选择了k个元素时，计算分数，统计分数的最大值，但是超时
• 参照题解，可以先将nums2从大到小进行排序，因为子序列中nums1和nums2的下标都是相同的，所以需要记录对nums2中的值进行排序后记录的是新下标newIdx
• 使用PriorityQueue存储子序列中nums1的元素，堆顶对应的是元素的最小值。在更换子序列的元素时，按照排好序的nums2将后续的元素newIdx加入进来，同时将之前子序列中某个元素弹出（不论弹出哪个元素nums2的最小值都是nums2[newIdx]），弹出的元素应该是子序列中nums1的最小值，也就是PriorityQueue的堆顶

代码

class Solution {
    public long maxScore(int[] nums1, int[] nums2, int k) {
        int n = nums1.length;
        Integer[] idxArr = new Integer[n];
        for (int i = 0; i < n; i++) {
            idxArr[i] = i;
        }
        // nums2从大到小进行排序，仅记录下标位置
        Arrays.sort(idxArr, (x, y) -> (nums2[y] - nums2[x]));
        // 堆顶为最小值
        PriorityQueue<Integer> queue = new PriorityQueue<>((x, y) -> (x - y));
        long sum1 = 0;
        for (int i = 0; i < k; i++) {
            int idx = idxArr[i];
            sum1 += nums1[idx];
            queue.offer(nums1[idx]);
        }
        long res = sum1 * nums2[idxArr[k - 1]];
        for (int i = k; i < n; i++) {
            // 此时nums2[idx]是nums2中子序列的最小值
            // 满足上述条件且nums1中相应子序列和最大：加上idx处的元素值，减去前面子序列中的最小元素
            int idx = idxArr[i];
            // nums2[idx]也比之前的子序列小，sum1也比之前的子序列小，分数一定更小，不考虑
            if (nums1[idx] < queue.peek()) {
                continue;
            }
            sum1 -= queue.poll();
            sum1 += nums1[idx];
            queue.offer(nums1[idx]);
            res = Math.max(res, sum1 * nums2[idx]);
        }
        return res;
    }
}

关键点

• 将nums2中的元素从大到小进行排序，初始选择k个元素，对应nums2最小值就是nums2[k - 1]，按顺序加入元素，弹出之前某个元素，保证快速找到子序列中nums2的最小值
• 根据nums2选择好子序列后，根据其下标将nums1中对应元素添加到PriorityQueue中（堆顶为最小值），保证快速找到nums2[newIdx]是最小值时nums1的元素和最大的子序列
• 如果加入新的元素下标对应在nums1中的元素值比PriorityQueue堆顶元素更小，说明此时分数一定比上一个子序列分数更低（nums1子序列之和更小，nums2子序列中的最小值也更小），不考虑