前言
在这篇文章中,我们一起来看看我们生活中都会用到,但却不那么熟悉的数据结构——图(英语:graph)。我们看下百科定义:
在计算机科学中,图(英语:graph)是一种抽象数据类型,用于实现数学中图论的无向图和有向图的概念。
图的数据结构包含一个有限(可能是可变的)的集合作为节点集合,以及一个无序对(对应无向图)或有序对(对应有向图)的集合作为边(有向图中也称作弧)的集合。节点可以是图结构的一部分,也可以是用整数下标或引用表示的外部实体。
图的数据结构还可能包含和每条边相关联的数值(edge value),例如一个标号或一个数值(即权重,weight;表示花费、容量、长度等)。
从上面定义,我们知道图分为有向图和无向图,图是由顶点和边,还有可能权重。我们看看图在哪些方面有应用:交通运输规划,每个地方就是图的顶点,而每条路就是图的边;社交网络分析,每个用户就是顶点,而用户之间是否为好友就是边;互联网,每个网页就是顶点,而网页上跳转到其他网页就是边,我们每天使用的百度,谷歌搜索引擎实现其中用到很重要技术就是图。还有像电路设计,通信网络,计划与排程问题都用到了图数据结构来表示他们的关系。
起源(欧拉与柯尼斯堡的七桥问题)
十八世纪,在今天俄罗斯加里宁格勒市还被称为柯尼斯堡的年代。像其他许多大城市一样,一条大河(普列戈利亚河)穿城而过。柯尼斯堡除了被一分为二以外,还包含河中的两个岛屿,人们建有七座桥梁连接着不同的陆地。当时有一个著名的游戏谜题,就是在所有桥都只能走一遍的前提下,怎样才能把这片区域所有的桥都走遍?这个谜题成为当地人一项热衷的消遭运动,许多人声称已经找到了这样一条路径,但当被要求按照规则再走一遍时,却发现还是没有人能够做到。直到 1736 年,瑞士数学家莱昂哈德·欧拉给出了答案,他在论文《柯尼斯堡的七桥》中解释了其中的原因,证明这样的步行方式并不存在,并在文中提出和解决了一笔画问题。
莱昂哈德·欧拉(Leonhard Euler,1707年4月15日–1783年9月18日)是18世纪最杰出的数学家之一,同时也是物理学、天文学和工程学领域的重要贡献者。大家感兴趣可以看下号称数学最美公式之一的欧拉公式。
图论基础知识
图由节点(Vertex)和连接节点的边(Edge)组成。
节点(Vertex):图中的基本元素,也称为顶点。节点可以代表各种事物,如城市、人物、物体等。
边(Edge):连接图中两个节点的线,表示节点之间的关系。边可以是有向的(箭头指向特定的方向)或无向的(没有箭头,表示双向关系)。
度(Degree):节点的度是与其相连的边的数量。对于有向图,节点的度分为入度(In-Degree)和出度(Out-Degree),分别表示指向该节点的边的数量和从该节点出发的边的数量。
路径(Path):图中连接节点的一系列边构成的序列。路径的长度是指路径上的边的数量。如果路径中的所有节点都是不同的,则称该路径是简单路径。
环(Cycle):由图中一系列边构成的闭合路径,起点和终点相同,并且路径中的节点都是不同的。
连通性(Connectivity):一个图被称为连通的,如果从图中的任意一个节点到另一个节点都存在至少一条路径。如果一个图不是连通的,则可以分为多个连通分量。
图的类型:根据图中边的性质,图可以分为有向图(Directed Graph)和无向图(Undirected Graph)。此外,图还可以是加权的,即边上带有权重(Weight)。
邻接矩阵(Adjacency Matrix)和邻接表(Adjacency List):这两种数据结构用于表示图的连接关系。邻接矩阵是一个二维数组,其中的元素表示节点之间是否相连。邻接表是由一组链表或数组构成的数据结构,用于表示每个节点的邻居节点。
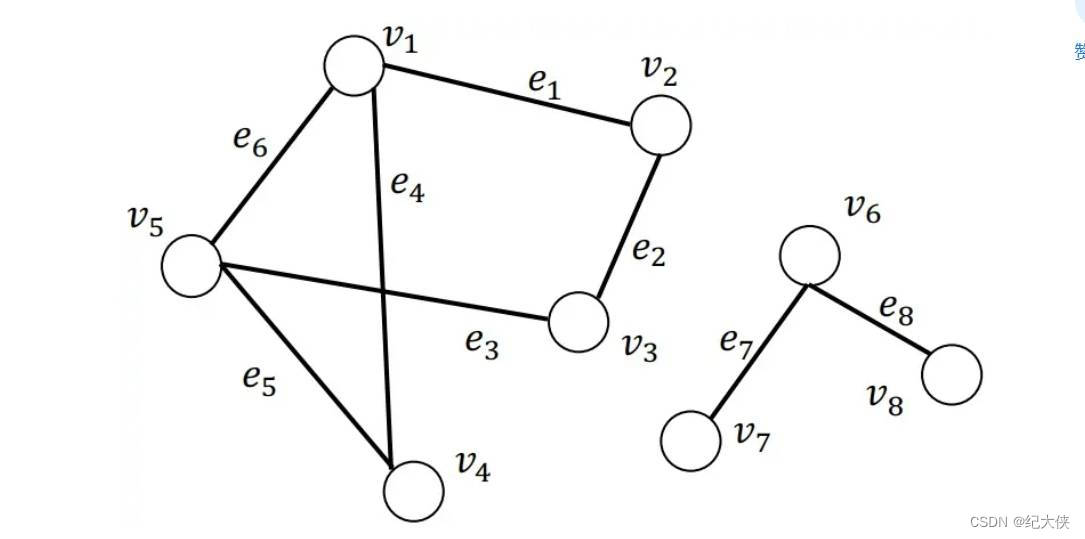
上图我们发现,右边就是我们熟悉的图。那么图在什么情况下能叫做树。
树是一种特殊的无向图。
无向图:树是一种无向图,其中任意两个节点之间都有唯一的简单路径。
连通图:树是连通图,即从任意一个节点出发,都可以到达图中的所有其他节点。换句话说,树是一个连通且无环的图。
无回路:树不包含回路,即没有形成环的路径。每个节点都只能通过一条路径到达另一个节点,因此树不会出现闭合的环路。
N个节点的树有N-1条边:如果一个无向图含有N个节点,并且是树的话,那么它必然有N-1条边。这个特性被称为树的性质之一。
图表示方式
**邻接矩阵(Adjacency Matrix)和邻接表(Adjacency List)**是两种常用的图表示方法,它们各自有自己的优缺点:
邻接矩阵的优缺点:
优点:
直观易懂:邻接矩阵直观地展示了图中节点之间的连接关系,易于理解和实现。
快速查找:可以在O(1)的时间内查找两个节点之间是否有边相连。
适用于稠密图:对于边的数量较多的稠密图,邻接矩阵的空间复杂度较低,使用更为高效。
缺点:
空间复杂度高:邻接矩阵需要使用N^2的空间来存储N个节点的连接关系,对于稀疏图来说,会浪费大量空间。
不适用于大规模图:当图规模很大时,邻接矩阵的空间开销会变得非常巨大,导致内存不足或效率低下。
无法存储边的权重:如果图中的边有权重,邻接矩阵需要额外的空间来存储这些权重信息,增加了复杂度。
下面是用Java实现邻接矩阵表示图
import java.util.Arrays;
public class AdjacencyMatrix {
private int[][] matrix;
private int numVertices;
public AdjacencyMatrix(int numVertices) {
this.numVertices = numVertices;
matrix = new int[numVertices][numVertices];
}
// 添加边
public void addEdge(int src, int dest) {
matrix[src][dest] = 1;
matrix[dest][src] = 1; // 无向图,所以需要反向也设置为1
}
// 删除边
public void removeEdge(int src, int dest) {
matrix[src][dest] = 0;
matrix[dest][src] = 0; // 无向图,所以需要反向也设置为0
}
// 打印邻接矩阵
public void printMatrix() {
for (int i = 0; i < numVertices; i++) {
System.out.println(Arrays.toString(matrix[i]));
}
}
public static void main(String[] args) {
int numVertices = 5;
AdjacencyMatrix graph = new AdjacencyMatrix(numVertices);
// 添加边
graph.addEdge(0, 1);
graph.addEdge(0, 4);
graph.addEdge(1, 2);
graph.addEdge(1, 3);
graph.addEdge(1, 4);
graph.addEdge(2, 3);
graph.addEdge(3, 4);
// 打印邻接矩阵
graph.printMatrix();
}
}
邻接表的优缺点:
优点:
空间利用率高:邻接表只存储有连接关系的节点,对于稀疏图来说,空间利用率更高。
易于插入和删除边:在邻接表中,插入或删除边的操作更为高效,时间复杂度为O(1)。
适用于稀疏图:对于边的数量较少的稀疏图,邻接表的空间复杂度更低,更加节省内存空间。
缺点:
查找边的时间复杂度高:在邻接表中查找两个节点之间是否有边相连,时间复杂度为O(n),其中n为节点的度数。
不适用于密集图:对于边的数量较多的密集图,邻接表的空间复杂度会增加,效率较低。
不适合快速查找:如果需要频繁进行两个节点之间是否相连的查找操作,邻接表的效率可能不如邻接矩阵。
下面是用Java实现表示邻接表
import java.util.*;
public class AdjacencyList {
private Map<Integer, List<Integer>> adjList;
public AdjacencyList() {
adjList = new HashMap<>();
}
// 添加节点
public void addNode(int node) {
adjList.put(node, new LinkedList<>());
}
// 添加边
public void addEdge(int src, int dest) {
adjList.get(src).add(dest);
adjList.get(dest).add(src); // 无向图,所以需要反向也添加
}
// 删除边
public void removeEdge(int src, int dest) {
adjList.get(src).remove((Integer) dest);
adjList.get(dest).remove((Integer) src); // 无向图,所以需要反向也删除
}
// 打印邻接表
public void printList() {
for (Map.Entry<Integer, List<Integer>> entry : adjList.entrySet()) {
System.out.print(entry.getKey() + " -> ");
for (Integer neighbor : entry.getValue()) {
System.out.print(neighbor + " ");
}
System.out.println();
}
}
public static void main(String[] args) {
AdjacencyList graph = new AdjacencyList();
// 添加节点
for (int i = 0; i < 5; i++) {
graph.addNode(i);
}
// 添加边
graph.addEdge(0, 1);
graph.addEdge(0, 4);
graph.addEdge(1, 2);
graph.addEdge(1, 3);
graph.addEdge(1, 4);
graph.addEdge(2, 3);
graph.addEdge(3, 4);
// 打印邻接表
graph.printList();
}
}
最短路径算法
图的最短路径算法用于找到两个节点之间的最短路径。
迪杰斯特拉算法(Dijkstra Algorithm)
package demo.algorithm.algorithm;
import java.util.*;
/**
*最短路径算法-迪杰斯特拉(Dijkstra)算法(1956年发表)
* 迪杰斯特拉(Dijkstra)算法是典型最短路径算法,用于计算一个节点到其他节点的最短路径。
* Dijkstra 算法是一个基于「贪心」、「广度优先搜索」、「动态规划」求一个图中一个点到其他所有点的最短路径的算法,时间复杂度 O(n2)
* 每次从 「未求出最短路径的点」中 取出 距离距离起点 最小路径的点,以这个点为桥梁 刷新「未求出最短路径的点」的距离
* 迪杰斯特拉(Dijkstra)算法,能处理有环图,不能处理含有负权边的图.
*
* 如果存在负权重,则可能在之后的计算中得到总权重更小的路径,从而影响之前的结果(译注:即可能出现多绕路反而路线更短的情况,不合实际)。
* @author jishenglong on 2023/1/24 9:14
**/
public class DijkstraAlgorithm {
private static final int INF = Integer.MAX_VALUE; // 无穷大表示不可达
public static void dijkstra(int[][] graph, int start, int end) {
int n = graph.length; // 图的顶点数
int[] dist = new int[n]; // 存储起始点到各个顶点的最短距离
boolean[] visited = new boolean[n]; // 标记顶点是否已访问
int[] prev = new int[n]; // 记录最短路径中的前驱顶点
// 初始化距离数组和前驱数组
Arrays.fill(dist, INF);
Arrays.fill(prev, -1);
dist[start] = 0;
// 开始算法
for (int i = 0; i < n - 1; i++) {
int minDist = INF;
int minIndex = -1;
// 找到当前未访问顶点中距离起始点最近的顶点
for (int j = 0; j < n; j++) {
if (!visited[j] && dist[j] < minDist) {
minDist = dist[j];
minIndex = j;
}
}
System.out.println(String.format("minIndex:%s,minDist:%s",minIndex,minDist ));
// 标记该顶点为已访问
visited[minIndex] = true;
// 更新与该顶点相邻顶点的最短距离和前驱顶点
for (int j = 0; j < n; j++) {
if (!visited[j] && graph[minIndex][j] != INF) {
int newDist = dist[minIndex] + graph[minIndex][j];
if (newDist < dist[j]) {
dist[j] = newDist;
prev[j] = minIndex;
}
}
}
}
System.out.println("cost: " + dist[end]);
// 打印最短路径
printShortestPath(prev, start, end);
}
// 递归打印最短路径
private static void printShortestPath(int[] prev, int start, int end) {
if (end == start) {
System.out.print(start);
} else if (prev[end] == -1) {
System.out.println("No path exists from " + start + " to " + end);
} else {
printShortestPath(prev, start, prev[end]);
System.out.print(" -> " + end);
}
}
public static void main(String[] args) {
int[][] graph = {
{0, 4, 2, INF, INF},
{4, 0, 1, 5, INF},
{2, 1, 0, 8, 10},
{INF, 5, 8, 0, 2},
{INF, INF, 10, 2, 0}
};
int start = 0; // 起始点
int end = 3; // 终点
dijkstra(graph, start, end);
}
}
Floyd算法
package demo.algorithm.algorithm;
/**
* 最短路径算法
* Floyd算法是一个经典的动态规划算法,它又被称为插点法。该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。
* Floyd算法是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法,算法目标是寻找从点i到点j的最短路径。
* 时间复杂度:O(n^3);空间复杂度:O(n^2)
* 弗洛伊德算法是解决任意两点间的最短路径的一种算法,可以正确处理有向图或有向图或负权(但不可存在负权回路)的最短路径问题,同时也被用于计算有向图的传递闭包
*
* @author jishenglong on 2023/1/24 9:51
**/
public class FloydAlgorithm {
private int numVertices;
private int[][] distance;
public FloydAlgorithm(int numVertices) {
this.numVertices = numVertices;
this.distance = new int[numVertices][numVertices];
// 初始化距离矩阵,表示顶点之间的初始距离
for (int i = 0; i < numVertices; i++) {
for (int j = 0; j < numVertices; j++) {
if (i == j) {
distance[i][j] = 0; // 顶点到自身的距离为0
} else {
distance[i][j] = Integer.MAX_VALUE; // 初始化为无穷大
}
}
}
}
// 添加边和权重
public void addEdge(int source, int destination, int weight) {
distance[source][destination] = weight;
// 如果是有向图,注释掉下一行
distance[destination][source] = weight;
}
/**
* 佛洛伊德算法的核心方法
* 在三重循环的每一次迭代中,我们检查通过中间顶点 k 是否能够获得更短的路径。
* 具体操作是检查从顶点 i 到顶点 k 的路径与从顶点 k 到顶点 j 的路径之和是否小于从顶点 i 到顶点 j 的当前已知路径。如果是,则更新最短路径
* <p>
* 外层循环 (k): 该循环遍历所有可能的中间顶点。在每次迭代中,k 表示中间顶点,我们尝试看看通过中间顶点是否能够找到更短的路径。
* 第一层内层循环 (i): 该循环遍历所有可能的起始顶点。
* 第二层内层循环 (j): 该循环遍历所有可能的目标顶点
*/
public void floydWarshall() {
// 三重循环,依次考虑每个顶点作为中间点的情况
for (int k = 0; k < numVertices; k++) {
for (int i = 0; i < numVertices; i++) {
for (int j = 0; j < numVertices; j++) {
if (distance[i][k] != Integer.MAX_VALUE && distance[k][j] != Integer.MAX_VALUE &&
distance[i][k] + distance[k][j] < distance[i][j]) {
distance[i][j] = distance[i][k] + distance[k][j];
}
}
}
}
// 打印最短路径矩阵
printShortestPaths();
}
private void printShortestPaths() {
System.out.println("Shortest paths between all pairs of vertices:");
for (int i = 0; i < numVertices; i++) {
for (int j = 0; j < numVertices; j++) {
if (distance[i][j] == Integer.MAX_VALUE) {
System.out.print("INF\t");
} else {
System.out.print(distance[i][j] + "\t");
}
}
System.out.println();
}
}
public static void main(String[] args) {
int numVertices = 4;
FloydAlgorithm floydGraph = new FloydAlgorithm(numVertices);
floydGraph.addEdge(0, 1, 3);
floydGraph.addEdge(0, 2, 5);
floydGraph.addEdge(1, 2, 1);
floydGraph.addEdge(2, 3, 7);
floydGraph.floydWarshall();
}
}
当我们只要求一个节点到其他节点的最短路径那么迪杰斯特拉(Dijkstra)算法比较适合;如果要求任意两点间的最短路径那么Floyd算法比较适合。
K短路
有时候需求是需要展示从A点到B点,3条最短路径,也就是k短路。k短路问题,可以参考以下文章k 短路
package demo.algorithm.algorithm;
import java.util.ArrayList;
import java.util.List;
import java.util.PriorityQueue;
/**
* AStar K短路
* https://oi-wiki.org/graph/kth-path/
*
* @author jisl on 2023/12/20 15:54
**/
public class AStarKPaths {
// 定义常量:表示无穷大的边权值
final int inf = Integer.MAX_VALUE / 2;
// 声明变量:节点数量
int n;
// 声明数组:存储节点的启发式值
int[] H;
// 声明数组:记录节点在搜索过程中被访问的次数
int[] cnt;
// 声明变量:记录当前处理的正向边和逆向边的数量
int cur, cur1;
// 正向图的邻接表
int[] h; // 头结点
int[] nxt; // 下一条边的索引
int[] p; // 相邻节点的编号
int[] w; // 边的权重
// 逆向图的邻接表
int[] h1; // 头结点
int[] nxt1; // 下一条边的索引
int[] p1; // 相邻节点的编号
int[] w1; // 边的权重
// 声明数组:记录节点是否被访问过
boolean[] tf;
// 构造函数
public AStarKPaths(int vertexCnt, int edgeCnt) {
n = vertexCnt;
//数组从0开始,要定义访问到vertexCnt,那么数组长度需要+1
int vertexLen = vertexCnt + 1;
int edgeLen = edgeCnt + 1;
// 初始化数组
H = new int[vertexLen];
cnt = new int[vertexLen];
h = new int[vertexLen];
nxt = new int[edgeLen];
p = new int[edgeLen];
w = new int[edgeLen];
h1 = new int[vertexLen];
nxt1 = new int[edgeLen];
p1 = new int[edgeLen];
w1 = new int[edgeLen];
tf = new boolean[vertexLen];
}
/**
* 添加正向图的边
*
* @param x 起点
* @param y 终点
* @param z 边的权重
*/
void addEdge(int x, int y, int z) {
// 当前边的索引
cur++;
// 将当前边的下一条边指向原来的头结点
nxt[cur] = h[x];
// 更新头结点为当前边的索引
h[x] = cur;
// 记录相邻节点和边的权重
p[cur] = y;
w[cur] = z;
}
/**
* 添加逆向图的边
*
* @param x 起点
* @param y 终点
* @param z 边的权重
*/
void addEdge1(int x, int y, int z) {
// 当前逆向边的索引
cur1++;
// 将当前逆向边的下一条边指向原来的逆向头结点
nxt1[cur1] = h1[x];
// 更新逆向头结点为当前逆向边的索引
h1[x] = cur1;
// 记录逆向相邻节点和边的权重
p1[cur1] = y;
w1[cur1] = z;
}
/**
* 节点类,用于A*算法中表示搜索过程中的节点
*/
class Node implements Comparable<Node> {
int x, v; // 节点编号和从起点到该节点的累计代价
List<Integer> path; // 存储路径
/**
* 构造方法,初始化节点
*
* @param x 节点编号
* @param v 从起点到该节点的累计代价
* @param path 从起点到该节点的路径
*/
Node(int x, int v, List<Integer> path) {
this.x = x;
this.v = v;
this.path = new ArrayList<>(path);
this.path.add(x); // 将当前节点加入路径
}
/**
* 优先队列比较方法,根据节点的估值(v + H[x])升序排序
*
* @param a 另一个节点
* @return 比较结果,1表示大于,-1表示小于
*/
@Override
public int compareTo(Node a) {
return v + H[x] > a.v + H[a.x] ? 1 : -1;
}
}
PriorityQueue<Node> q = new PriorityQueue<>();
/**
* 节点类,用于Dijkstra算法中表示搜索过程中的节点
*/
class Node2 implements Comparable<Node2> {
int x, v; // 节点编号和从起点到该节点的累计代价
/**
* 构造方法,初始化节点
*
* @param x 节点编号
* @param v 从起点到该节点的累计代价
*/
Node2(int x, int v) {
this.x = x;
this.v = v;
}
/**
* 优先队列比较方法,根据节点的累计代价(v)升序排序
*
* @param a 另一个节点
* @return 比较结果,1表示大于,-1表示小于
*/
@Override
public int compareTo(Node2 a) {
return v > a.v ? 1 : -1;
}
}
PriorityQueue<Node2> Q = new PriorityQueue<>();
/**
* 构建图并执行 A* K 短路算法
*
* @param graph 图的邻接矩阵,表示节点间的边权值
* @param s 起点(source)
* @param t 目标节点(target)
* @param k 要求的最短路径数量
*/
public void build(int[][] graph, int s, int t, int k) {
// 起点s、目标节点t、路径数量k等
// 读取图的边信息并构建正向图和逆向图
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (graph[i][j] != Integer.MAX_VALUE / 2) {
addEdge(i, j, graph[i][j]);
addEdge1(j, i, graph[i][j]);
}
}
}
// 初始化启发式数组H,使用逆向边进行估值
for (int i = 1; i <= n; i++) {
H[i] = inf;
}
// 使用 Dijkstra 算法计算从目标节点 t 到其他节点的估值 H
Q.add(new Node2(t, 0));
while (!Q.isEmpty()) {
Node2 x = Q.poll();
if (tf[x.x]) {
continue;
}
tf[x.x] = true;
// 启发式数组H 在Node节点比较的时候使用
H[x.x] = x.v;
for (int j = h1[x.x]; j != 0; j = nxt1[j]) {
Q.add(new Node2(p1[j], x.v + w1[j]));
}
}
// 使用 A* 算法计算从起点 s 到目标节点 t 的 k 条最短路径
q.add(new Node(s, 0, new ArrayList<>())); // 将起点 s 加入优先队列 q,初始累计代价为 0,路径为空列表
while (!q.isEmpty()) {
Node x = q.poll(); // 弹出当前累计代价最小的节点
cnt[x.x]++; // 增加当前节点的访问次数
if (x.x == t) {
// 如果当前节点是目标节点,输出 A* K 短路算法的相关信息,包括路径
System.out.println(String.format("AStarKPaths对应值:x.v=%s,cnt[x.x]=%s,path=%s", x.v, cnt[x.x], getPath(x.path, s, t)));
}
if (x.x == t && cnt[x.x] == k) {
System.out.println(x.v); // 如果找到第 k 条最短路径,输出累计代价并结束
return;
}
if (cnt[x.x] > k) {
continue; // 如果当前节点访问次数超过 k,跳过后续处理
}
for (int j = h[x.x]; j != 0; j = nxt[j]) {
q.add(new Node(p[j], x.v + w[j], new ArrayList<>(x.path))); // 将该节点的邻接节点加入优先队列,并更新累计代价和路径
}
}
System.out.println("-1");
}
private String getPath(List<Integer> path, int a, int b) {
StringBuilder result = new StringBuilder();
result.append("Shortest distance from ").append(a).append(" to ").append(b).append(": ");
for (int i = 0; i < path.size(); i++) {
result.append(" -> ").append(path.get(i));
}
result.append("\n==================================");
return result.toString();
}
public static void main(String[] args) {
int INF = Integer.MAX_VALUE / 2;
int[][] graph = {
{INF, 4, 2, INF, INF},
{4, INF, 6, 5, INF},
{2, 1, INF, 8, 10},
{INF, 5, 8, INF, 2},
{INF, INF, 10, 2, INF}
};
final AStarKPaths aStarKPaths = new AStarKPaths(graph.length, graph.length * graph.length);
aStarKPaths.build(graph, 0, 3, 3);
}
}
总结
以上简单介绍了,图论知识。对于图论中用的比较多最短路和k短路用Java实现了。实际图论是比较难的问题,这边只是做了简单的介绍,抛砖引玉。