第二章.线性回归以及非线性回归

2.8 标准方程法

1.公式

1).代价函数：

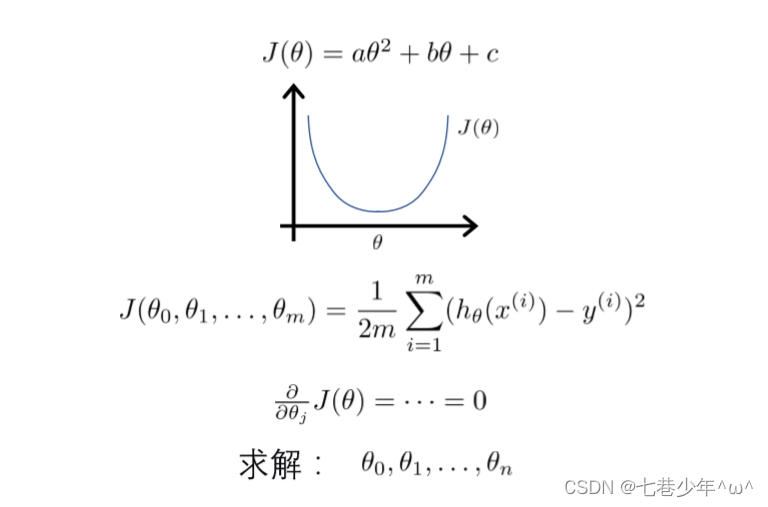
2).累加平方和用矩阵表示：

2.对(𝑦 − 𝑋𝑤)^𝑇(𝑦 − 𝑋𝑤)求导的两种布局方式：

1).分子布局(Numerator-layout)

• 分子为列向量或者分母为行向量

2).分母布局(Denominator-layout)

• 分子为行向量或者分母为列向量

• 公式推导
  
  
  

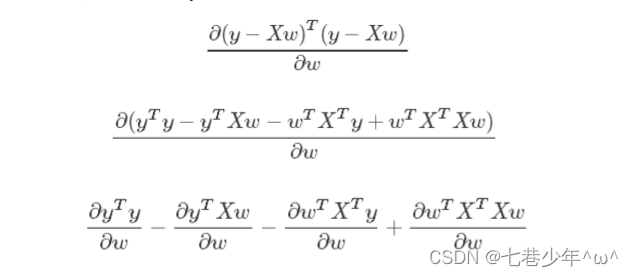
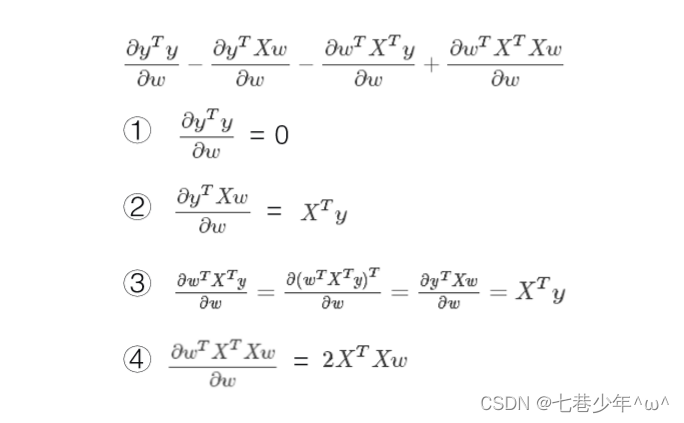
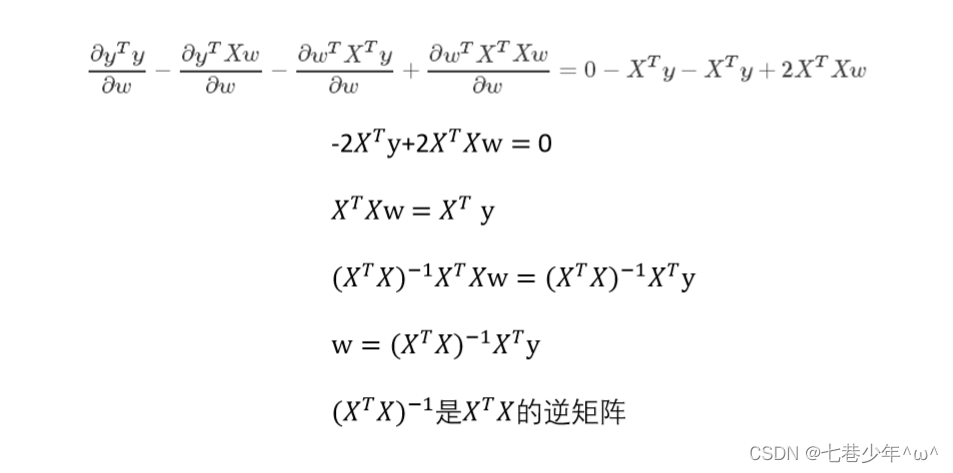
• 维基百科中的求导公式：
  

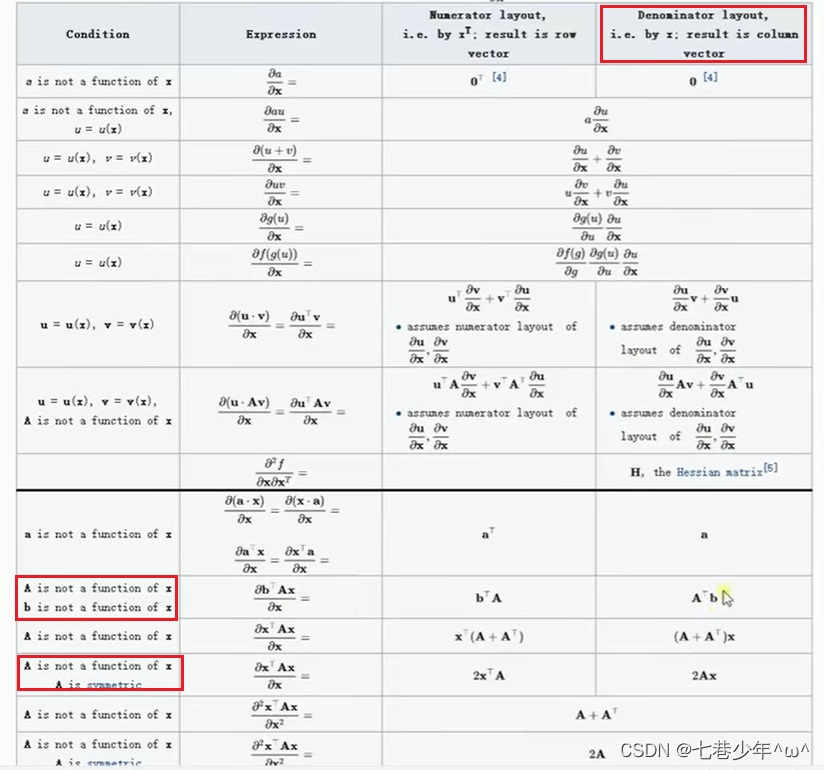
3.矩阵不可逆的情况：

• 线性相关的特征（多重公用性）

• 特征数据太多（样本数m<=特征数n）

4.梯度下降法VS标准方程法：

/	梯度下降法	标准方程法
优点	当特征值非常多的时候也可以很好的工作	1).不需要学习率; 2).不需要迭代； 3).可以得到全局最优解；
缺点	1).需要选择合适的学习率; 2).需要迭代很多个周期； 3).只能得到最优解的近似值；	1).需要计算(X T X)−1 ; 2).时间复杂度大约是O(n3)，n是特征数量；

说明：sklearn中封装的线性回归模型是标准方程法，而不是梯度下降法

5.实战： 标准方程法

1).CSV中的数据：

• data.xlsx
• 上传文件为excel文件，需转换成csv文件使用

2).代码

import numpy as np
import matplotlib.pyplot as plt

# 加载数据
data = np.loadtxt('D:\\data\\data.csv', delimiter=',')
# 数据切片并增加一个维度
x_data = data[:, 0, np.newaxis]
y_data = data[:, 1, np.newaxis]

# 样本增加偏置项
X_data = np.concatenate((np.ones((100, 1)), x_data), axis=1)


# 标准方程法求解回归参数
def weights(xArr, yArr):
    xMat = np.mat(xArr)
    yMat = np.mat(yArr)
    # 矩阵乘法
    xTx = xMat.T * xMat
    # 判断该矩阵是否存在逆矩阵
    if np.linalg.det(xTx) == 0.0:
        print("This matrix cannot do inverse")
        return

    return xTx.I * xMat.T * yMat


ws = weights(X_data, y_data)
print('参数：', ws)

# 画图
x_test = np.array([[20], [80]])
y_test = x_test * ws[1] + ws[0]
plt.plot(x_data, y_data, 'b.')
plt.plot(x_test, y_test, 'r')
plt.show()

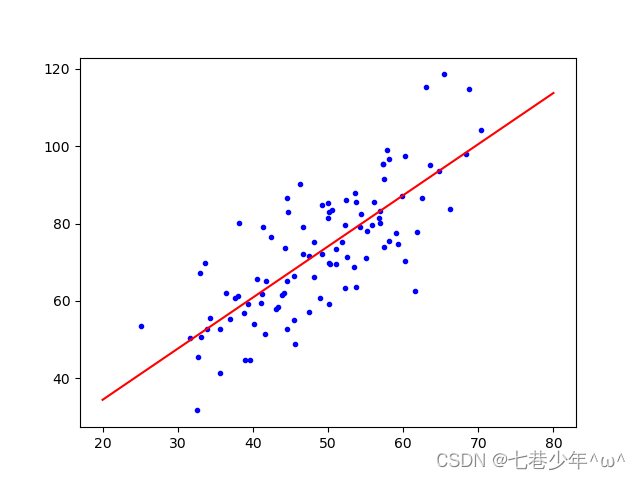
3).结果展示：

①.数据

②.图像