经典dp（最长公共序列）

最长公共子序列__牛客网

解析：

有两个字符串T和S，S的长度为n T的长度为m

状态：f[i][j] 表示n的前 i 个字母，和m的前 j 个字母的最长公共子序列长度

情况一：s[i]==t[i]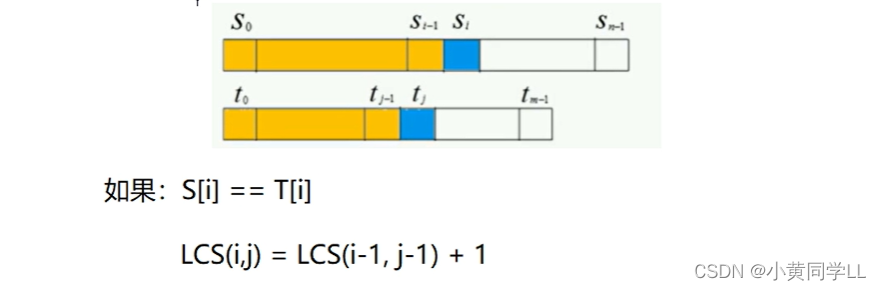

因为两个字符相同，所以该最长公共子序列==除这两个字符外的最长公共子序列+1；

即f[i][j]==f[i-1][j-1]+1;

情况二：s[i]!=t[i]

如果两个字符不同，则最长序列可能在只包含si或ti的组合串中；

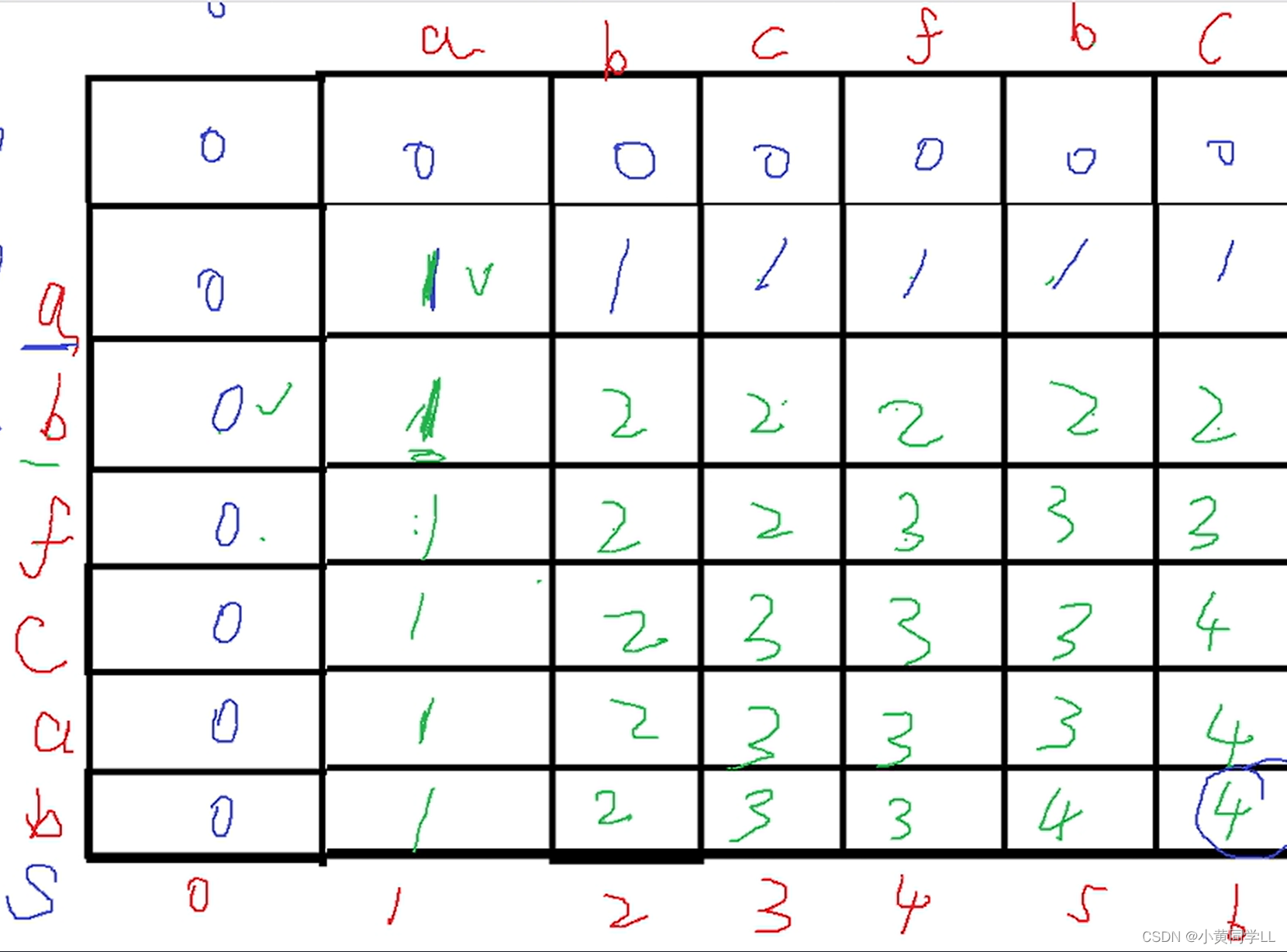
// 参考自id：没有头的小蘑菇
#include<iostream>
#include<cstring>
#include<vector>
using namespace std;
//int dp[110][110];

int main()
{
    string s1, s2;
    while(cin>>s1>>s2)
    {
        vector<vector<int>> dp(s1.size()+1,vector<int>(s2.size()+1, 0));
        //memset(dp,0,sizeof dp);
        for(int i = 1; i <= s1.size(); i++)
            for(int j = 1; j<= s2.size(); j++)
            {
                if(s1[i-1] == s2[j-1])
                    dp[i][j] = dp[i-1][j-1]+1;
                else
                    dp[i][j] = max(dp[i-1][j],dp[i][j-1]);
            }
        cout<<dp[s1.size()][s2.size()]<<endl;
    }
    return 0;
}

经典dp（最长上升子序列）

最长上升子序列__牛客网

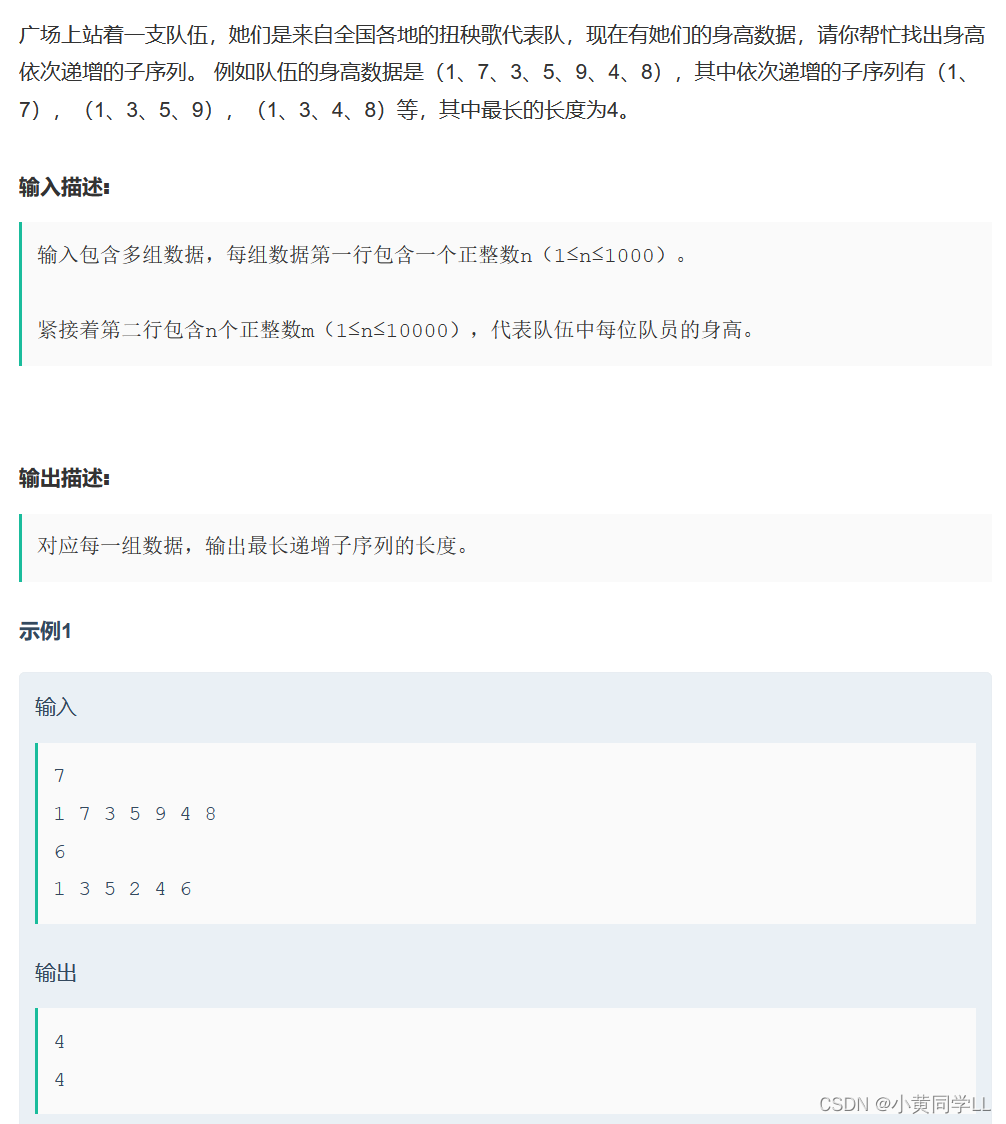
【解题思路】

动态规划的难点在于定义数组和创建“状态转移方程”。

1. 定义height来存储数据，f[i]为以height[i]结尾的元素的最长上升子序列元素个数，初始时

将f所有内容全部初始化成1，因为子序列中至少包含一个元素。

状态表示：f[i]表示从第一个数字开始算，以height[i]结尾的最大的上升序列。(以height[i]结尾的所有上升序列中属性为最大值的那一个)

状态计算（集合划分）：j∈(0,1,2,..,i-1), 在height[i] >height[j]时，
f[i] = max(f[i], f[j] + 1)。
有一个边界，若前面没有比i小的，f[i]为1（自己为结尾）。

最后在找f[i]的最大值。

// write your code here cpp
#include <iostream>
#include <vector>
using namespace std;
int main(){
    int n;
    while(cin >> n){
        vector<int> height(n, 0);
        for(int i = 0; i < n; i ++){
            cin >> height[i];
        }
        
        vector<int> f(n, 1);//初始每个数字长度为1
        int result = 1;
        for(int i = 1; i < n; i ++){
            for(int j = 0; j < i; j ++){
                if(height[i] > height[j])//说明该数字比该序列所有数字大
                {
                    f[i] = max(f[i], f[j] + 1);//f[j]+1将这个数字放在序列前面
                }
            }
            result = max(result, f[i]);
        }
        
        cout << result << endl;
    }
}

非dp巧妙写法

// write your code here cpp

#include <iostream>
#include <vector>
using namespace std;

int main()
{
    int n;
    while(cin >> n)
    {
        vector<int> ret;
        int num;
        int i;
        while(n--)
        {
            cin >> num;
            i = 0;
            for(; i < ret.size(); ++i)
            {
                if(num <= ret[i])
                {
                    ret[i] = num;
                    break;
                }
            }
            if(i == ret.size())
                ret.push_back(num);
        }
        
        cout << ret.size() << endl;
    }
}