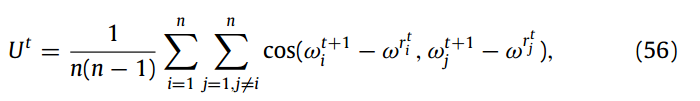基于Matplotlib的模型性能可视化工作

news2024/11/17 3:00:30

一、项目简介

本项目是科技考古墓葬识别工作的中间过程，因为需要大量复用所以另起一章好了。

主要涉及到数据读取、数据可视化和少量的数据处理过程。

二、相关知识

Pandas
Matplotlib

三、实验过程

1. 数据探索性分析

1.1 准备工作–导入模块

import pandas as pd
import os
import numpy as np 
import matplotlib.pyplot as plt

1.2 数据预处理

我们首先构建一个色彩映射表，这个表将由一组自定义的颜色条构成，并且对应一个索引值，以便我们按照强度自定义生成绘图颜色。

可以在网址上对你想要的颜色生成色度条。

colorMap=dict(zip(range(len(ModelMap),-1,-1),[
     "#d16ba5",
    "#c777b9", 
    "#ba83ca", 
    "#aa8fd8", 
    "#9a9ae1", 
    "#8aa7ec",
    "#79b3f4",
    "#69bff8",
    "#52cffe",
    "#41dfff", 
    "#46eefa", 
    "#5ffbf1"
]))

这个优势在于手动调整，不想怎么做可以使用各种可视化模块里自带的色彩映射cmap。

然后就是将训练的模型信息输入到一个字典中，这里k,v值分别是模型名称、(模型参数量，模型平均精度)。

ModelMap={
    "YOLOv5-n":[1.9,0.7],
    "YOLOv5-s":[7.2,0.782],
    "YOLOv5-m":[21.2,0.777],
    "YOLOv5-l":[46.5,0.746],
    "YOLOv5-x":[86.7,0.768],
    "YOLOv8-n":[3.2,0.764],
    "YOLOv8-s":[11.2,0.813],
    "YOLOv8-m":[25.9,0.7],
    "YOLOv8-l":[43.7,0.7],
    "YOLOv8-x":[68.2,0.7]
}

我们想要将模型参数量从小到大排布，以便确定最优性能，那么可以使用sort方法进行排序：

newSort=list(ModelMap.items())
newSort.sort(key=lambda x:x[1][1],reverse=True)

这里面的reverse=True表示降序排序，这里等于是以模型的精度进行排序。注意lambda表达式，:前表示输入，后表示返回值。

结果应该如下所示。

[('YOLOv8-s', [11.2, 0.813]),
 ('YOLOv5-s', [7.2, 0.782]),
 ('YOLOv5-m', [21.2, 0.777]),
 ('YOLOv5-x', [86.7, 0.768]),
 ('YOLOv8-n', [3.2, 0.764]),
 ('YOLOv5-l', [46.5, 0.746]),
 ('YOLOv5-n', [1.9, 0.7]),
 ('YOLOv8-m', [25.9, 0.7]),
 ('YOLOv8-l', [43.7, 0.7]),
 ('YOLOv8-x', [68.2, 0.7])]

2. 可视化

为了更加直观的比较模型性能，我们选择采用二维散点图进行绘制。在此过程中，采用不同的颜色和尺寸可以让结果更加清晰直观。因此，我们选择了颜色和尺度两个额外维度，辅助可视化过程。

首先是获取尺度信息，这里采用的归一化缩放，为了让数据区间更加美观，选择采用np.clip(n,a,b)方法将数据区间变成(a,b)，并执行相应的放缩。

def getScale(x,k=9.5):
    return np.clip(((x-min(y))/(max(y)-min(y))),0.15,0.95)*k

2.1 绘制散点图

还记得我们之前构建的自定义色度条吗，现在我们将结合色度条和尺度信息来绘制散点图。

# 首先是设置好 Figure 大小
# 在matplotlib中，绘图将基于 figure canvas axis 进行
plt.figure(figsize=(16,8))

for i,(k,v) in enumerate(newSort):
	# label 表示标签
	# s表示尺寸信息
	# c表示色彩信息
	# alpha表示透明度通道信息
	plt.scatter(v[0],v[1],c=colorMap[i],label=k,s=getScale(v[1])**2*np.pi,alpha=1)

# 添加行列标签
plt.ylabel("AP")
plt.xlabel("Parameters (M)")

# 在右上显示图例
plt.legend(loc='upper right')
# 设置标题
plt.title("AP-Params of different Model structures")

# 设置 xaxis 范围
plt.xlim(0,120)
# 设置格网信息
plt.grid(alpha=0.1,linestyle="--")

for i,j in zip(x,y):
	# 标记，用的是annotate 方法
	# plt.annotate(text,loc,xytext,textcoords,ha)
	# 常用参数 text表示文本信息 loc表示坐标点位置
	# xytext表示文本偏移量 textcoords表示文本以什么为坐标
	# ha表示文本显示位置，一般这组参数可以不动，即
	
	# xytext=(0,10),textcoords="offset points",ha='center'
    plt.annotate("%s"%j,(i,j),xytext=(0,10),textcoords="offset points",ha='center')
plt.savefig(r"new.jpg")
    
plt.show()

在这里插入图片描述

此时图像如图所示，为了将同一类模型归类，我们还可以采用折线图进行辅助。

2.2 绘制折线图

for i,j in ModelMap.values():
    x.append(i)
    y.append(j)

plt.plot(x[:5],y[:5],label="YOLO-v5",linestyle=':',alpha=0.5)
plt.plot(x[5:],y[5:],label="YOLO-v8",linestyle=':',alpha=0.5)

结果如图所示：

在这里插入图片描述

2.3 绘制模型过程性参数

在本阶段，我们需要做的需求为：将训练过程中的精度、召回率以及mAP:0.5，mAP:0.5:0.95进行可视化。

可简要拆解为以下过程：

读取相关csv文件
构建文件映射，并且将每30epoch进行平均
基于matplotlib绘制
基于pyecharts进行绘制

为了方便读取csv文件，我们可以用os.listdir方式快速获取某一路径下的所有子文件，这个方法常常结合寻找后缀来用，譬如：

[i for i in os.listdir(path) if i.endswith('.csv')]

这里我们有两个大文件夹，先获取其路径：

yolov5=r"C:\Users\Administrator\Desktop\Train_Res\YOLO_V5"
yolov8=r"C:\Users\Administrator\Desktop\Train_Res\YOLO_V8"

然后构建csv文件列表：

data_list=[os.path.join(yolov5,i) for i in os.listdir(yolov5) if i.endswith('.csv')]+[os.path.join(yolov8,i) for i in os.listdir(yolov8) if i.endswith('.csv')]

与上述方法相同，当路径较多时，可写成迭代器形式。

接下来就是确定模型名称+csv文件了，用的是pd.read_csv，这里如果出现中文，可能需要加上pd.read_csv(encoding="utf-8")

dataMap={}
for i in data_list:
    fir,sec=i.find("_V")+2,i.find(".c")-1
    dataMap[f"yolov{i[fir]}_{i[sec]}"]=pd.read_csv(i)

注意这样的写法不具有泛用性，甚至改个位置就会报错，但是确实很快

查看我们的结果：

dataMap.keys()

# dict_keys(['yolov5_l', 'yolov5_m', 'yolov5_s', 'yolov5_x', 'yolov8_n', 'yolov8_s'])

已经拿到数据了，然后就是看看读取到的结果咋样：

dataMap['yolov5_x'].head()

在这里插入图片描述

成功。

下面来构造数据，由于有些模型采用了剪枝，在100epoches不收敛的情况下自动终止训练，所以数据的长度不一致。我们可以取其中最短的进行分析，不过这里用了360epoches。

请注意，确定你的模型在区间 $U(\delta)$ 内是陷入了局部最优解的，否则没有比较意义。

x=[i for i in range(0,360,15)]
# 获取列名
col=dataMap['yolov5_x'].columns

由于有多组参数需要比较，出于复用性考虑，我们采用函数的方式进行绘制：

def plotValue(idx,reset=None,ws=15):
    plt.figure(figsize=(20,8))
    for k,v in dataMap.items():
        v=v.iloc[:,idx]
        # 此时的平滑窗口是15
        plt.plot(x,[sum(v[i*ws:i*ws+ws])/ws for i in range(360//ws)],label=k)
    plt.xlabel("epoches")
    ylab=col[idx] if not reset else reset
    plt.ylabel(ylab)
    plt.title(f"{ylab} variation of different models")
    plt.legend()
    return plt