---

前言

在本篇文章中，我们将会讲到leetcode中15. 三数之和，我们将会用到双指针的方式解决这道问题，同时注意掌握算法原理的去重操作。

一、题目描述

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请

你返回所有和为 0 且不重复的三元组。

注意：答案中不可以包含重复的三元组。

示例 1：

输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]
解释：
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意，输出的顺序和三元组的顺序并不重要。
示例 2：

输入：nums = [0,1,1]
输出：[]
解释：唯一可能的三元组和不为 0 。
示例 3：

输入：nums = [0,0,0]
输出：[[0,0,0]]
解释：唯一可能的三元组和为 0 。

题目描述的可能没有那麽清晰，我们根据示例一具体看看。
🌟根据题目要求，我们需要在nums中找到三个数nums[ i ],nums[ j ]，nums[ k ],满足nums[ i ]+nums[ j ]+nums[ k ]=0;
并且i!=j!=k。
比如nums = [-1,0,1,2,-1,-4]
我们可以发现0+0+0=0;但这是不允许的，三个数必须是不同的位置。
🌟答案中不可以包含重复的三元组。
根据nums中内容，满足条件的是【-1，0，1】【0 ，1，-1】【-1，2，-1】；
nums中有两个-1，可组成【-1，0，1】【0 ，1，-1】，虽然顺序不同，但里面的内容确是一样的，我们只保留一个！！！

🌟输出的顺序我们并不需要关心

二、代码原理

1.暴力解法

我们是很容易想到用三层for循环解决的，但是还有一个问题！！！就是去重操作。
有人就想到了去重用unordered_set去重，但是如果里面的两个为【-1，0，1】【0 ，1，-1】，我们依然不能去重。

接下来解决问题的难题就是如何保证找出来满足条件的三个数是顺序排放的？？

我们对nums先进行排序就可以实现

时间复杂度O(N^3)

2.双指针优化

我们想想如何进行优化呢？？
我们对数组进行排序了，我们就优先考虑双指针和二分算法。

我们以nums={-4,-4,-1,0,0,0,3,4,4,5}为例

🌟固定一个数nums[ i ]=ret
🌟left=i+1,right=nums.size()-1;
🌟在left和right区间内寻找两个数，使两个数满足nums[ left ]+nums[ right ]=-ret;,我们找到一组满足条件的数据之后，继续向下寻找，直到left和right相遇为止。
🌟i++,继续寻找

解决去重问题

我们依然可以用unordered_set解决
我们想想还有没有更优的解法解决？？

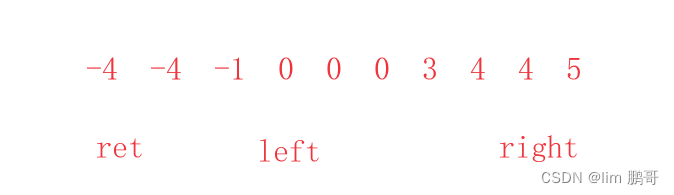
我们发现nums[ left ]=0;nums[ right ]=4,刚好满足题目要求.left++,right- -,这时继续向后寻找，我们发现nums[ left ]还是等于0，nums[ rigth ]还是等于4，同样满足条件。但是和刚才的数据是一样的，需要去重。

我们在这里就可以完成去重操作
🌟left跳过与前一个元素相同的元素
🌟right跳过与后一个元素相同的元素
🌟i其实也需要进行去重，跳过与前一个元素相同的元素

在去重时要防止越界
例如：nums = [0,0,0,0]

时间复杂度O（N^2）

三.代码编写

我们这里还有一个可以优化的地方，三个数相加等于0，说明其中一个数必然是小于等于0的，如果我们固定的那个数是大于0的，我们就不用再往下判断了，因为是有序的，后面的数肯定也是大于0的。不会找出满足条件的三个数。

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) 
    {
        //先排序
        sort(nums.begin(),nums.end());
        //寻找
        vector<vector<int>>vv;
        int n=nums.size();
        for(int i=0;i<n-2;)
        {
            //小优化
            if(nums[i]>0) break;
            int ret=-nums[i];
            int left=i+1;
            int right=n-1;
            while(left<right)
            {
                if(nums[left]+nums[right]>ret)
                {
                    right--;
                }
                else if(nums[left]+nums[right]<ret)
                {
                    left++;
                }
                else
                {
                    vv.push_back({nums[i],nums[left],nums[right]});
                    left++;right--;
                    //去重left
                    while(left<right&&nums[left]==nums[left-1])
                    {
                        left++;
                    }
                    //去重right
                      while(left<right&&nums[right]==nums[right+1])
                    {
                        right--;
                    }
                }
            }
            i++;
            //去重i
            while(i<n-2&&nums[i]==nums[i-1])
            {
                i++;
            }
    
        }
        return vv;
    }
};

总结

以上就是我们对Leetcode中15. 三数之和详细介绍，希望对大家的学习有所帮助，仅供参考 如有错误请大佬指点我会尽快去改正 欢迎大家来评论~~