一、Wallace树乘法器
Wallace树乘法器就是将多个部分积进行分组,每三个一组,最后如果剩下的部分积个数不够三个的不做处理,然后将各组的部分积进行相加得到和以及进位信息,直到最终只剩下两行部分积,相加后得到最终结果。
以下面的例子进行说明:
a=8'hA7,b=8'hD9
①首先列出所有的部分积,然后按照三个三个进行分组,如图中相同颜色的为一组,但是最后黄色的两个由于不够则不进行运算,然后对一组内的三行部分积进行运算,得到的和留在本位,得到的进位填充到前一列的最后一行,详见下图2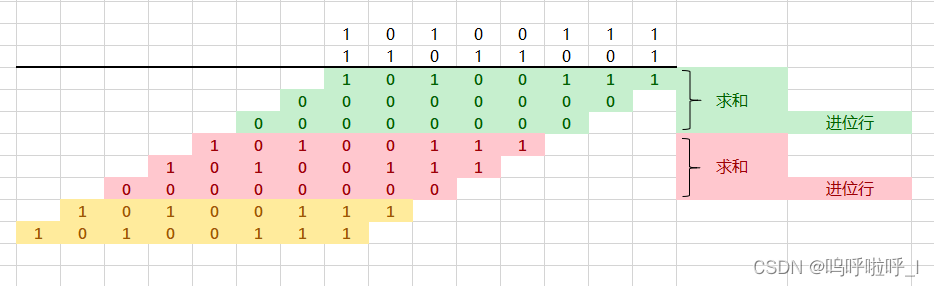
图1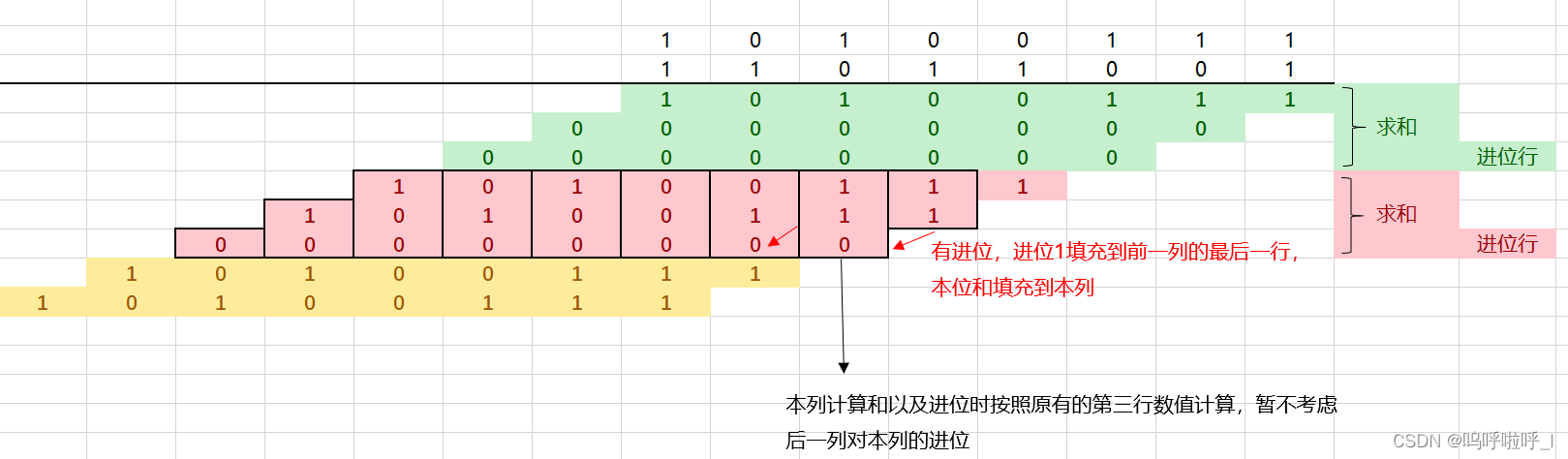
图2
在上图中,我们以红色部分的进行举例,三行的运算结果最终为两行,第一行为和,第二行为进位。
第一行红色背景的最后一列只有1,因此本位和为1,没有进位因此填充到前一列最后一行的为0 ;倒数第二列有两个1,因此本位和为0,进位为1填充到它的前一列的最后一行,后面同理,详见下图: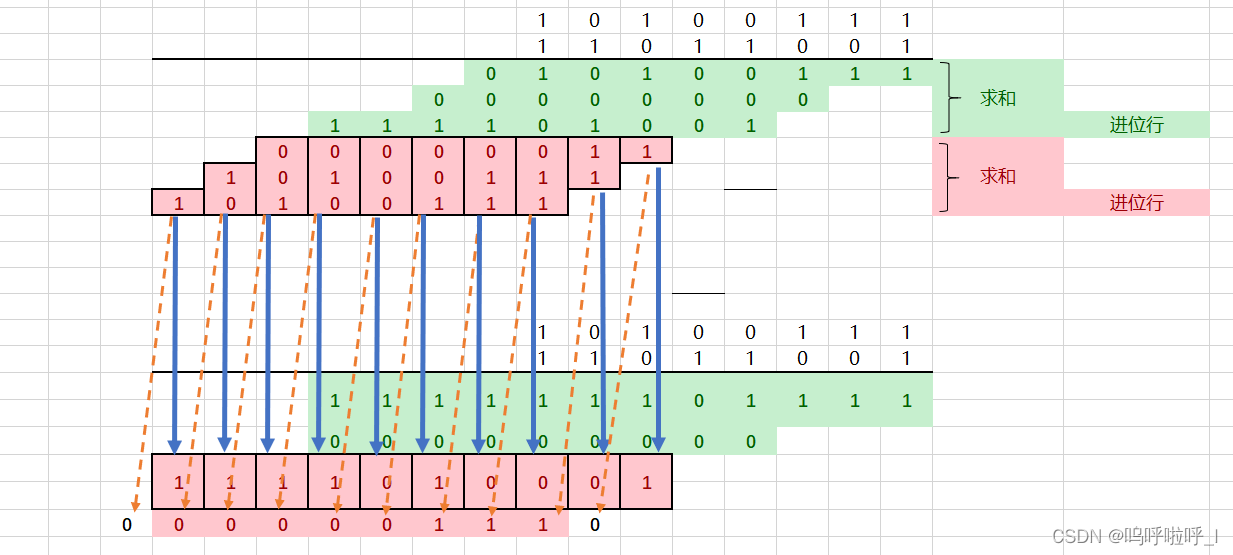
图3
图中蓝色箭头表示和的填充,黄色虚线箭头表示进位的填充,需要注意的是在此次计算中新产生的进位不参与运算,只填充到对应位置。
②将上述得到的结果再次分组,如图5
图4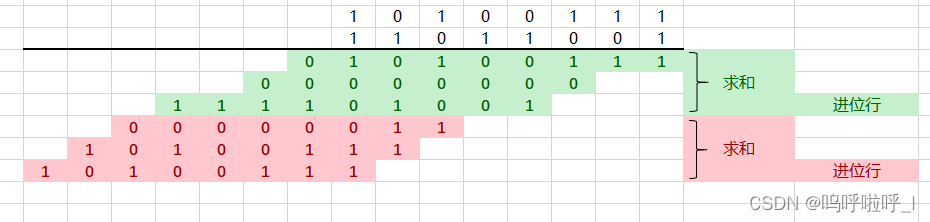
图5
③再次按照上述步骤计算得到图6,再分组得到图7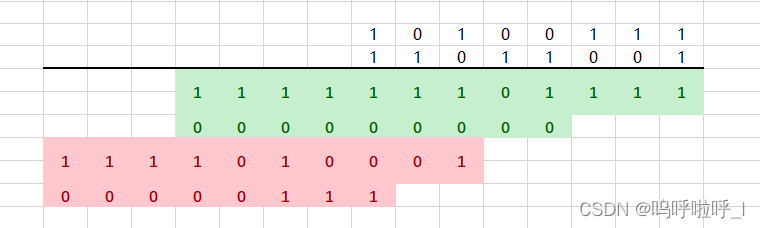
图6
图7
④计算得到结果然后再分组如图9
图8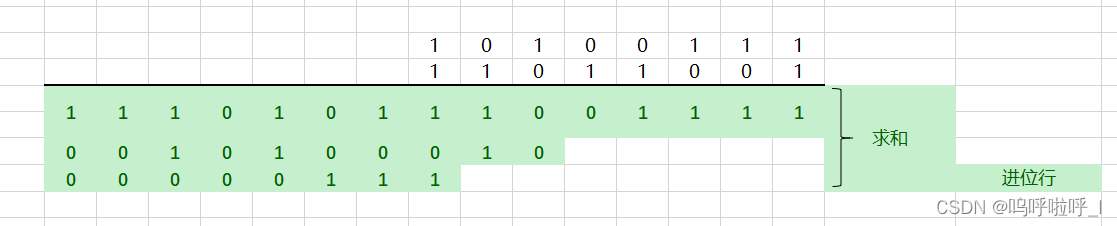
图9
⑤得到最后结果只剩两行,直接相加得到最终结果
二、Verilog实现
wallace_tree模块如下:
module wallace_tree(
input [3:0] a,
input [3:0] b,
input data_valid,
output [7:0] sum
);
reg [7:0]temp[3:0];
reg [7:0]temp_reg[3:0];
integer i;
integer j;
always@(*)
begin
if(data_valid)
for(i=0;i<=3;i=i+1)
begin
temp[i]=8'b0;
temp_reg[i]=8'b0;
for(j=0;j<=3;j=j+1)
begin
temp[i][j]=(a[j]&b[i]);
end
end
temp_reg[0]=temp[0];
temp_reg[1]=temp[1]<<1;
temp_reg[2]=temp[2]<<2;
temp_reg[3]=temp[3]<<3;
end
wire [7:0]cin_1;
wire [7:0]sum_1;
wire [7:0]cin_2;
wire [7:0]sum_2;
full_add inst_full_add (.a(temp_reg[0]), .b(temp_reg[1]), .c(temp_reg[2]), .cin(cin_1), .sum(sum_1));
full_add inst_full_add1 (.a(sum_1), .b(cin_1), .c(temp_reg[3]), .cin(cin_2), .sum(sum_2));
assign sum=cin_2+sum_2;
endmodule
full_add模块如下:
module full_add(
input [7:0]a,
input [7:0]b,
input [7:0]c,
output [7:0]cin,
output [7:0]sum
);
reg [7:0]cin=0;
reg [7:0]sum=0;
integer i;
always@(*)
begin
for(i=0;i<=7;i=i+1)
begin
sum[i]=a[i]^b[i]^c[i];
cin[i+1]=(a[i]&b[i])|((a[i]|b[i])&c[i]);
end
end
endmodule
仿真tb如下:
module tb_top();
reg [3:0]a;
reg [3:0]b;
wire [7:0]sum;
reg data_valid;
initial begin
a=0;b=0;
data_valid=0;
#100
a=4'b0011;
b=4'b1010;
data_valid=1;
#100
a=0;b=0;
data_valid=0;
#100
a=4'b1111;
b=4'b1111;
data_valid=1;
#100
a=0;b=0;
data_valid=0;
#100
a=4'b1100;
b=4'b1100;
data_valid=1;
#100
a=0;b=0;
data_valid=0;
end
wallace_tree inst_multiplication (.a(a), .b(b), .data_valid(data_valid), .sum(sum));
endmodule
仿真结果如下: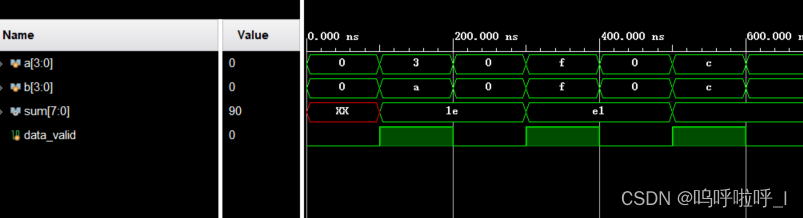
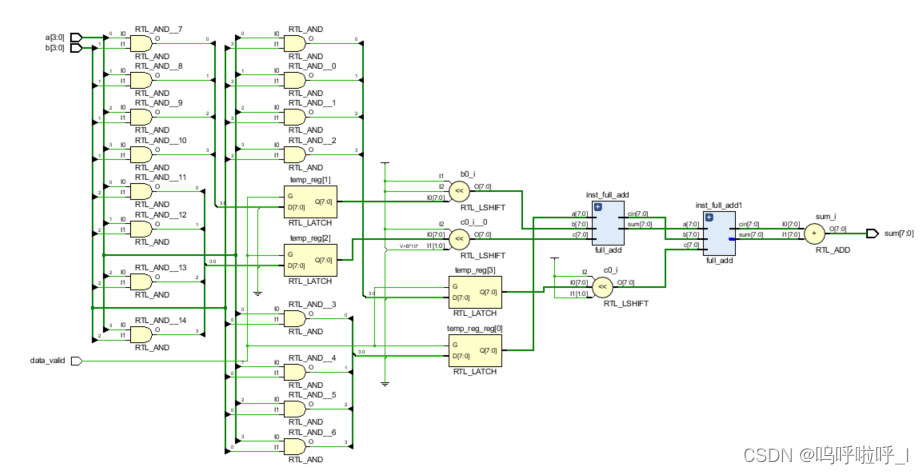
综合结果如下: