一、等差数列划分
413. 等差数列划分

算法原理

💡细节:
1.如果当前nums数组中i位置的数和前面两个数可以构成等差数列,那么当前位置所有子数组构成的等差数列个数dp[i]就等于前一个位置有子数组构成的等差数列个数+1(这个1代表增加最后三个数构成的等差数列)【简单理解:就是以a和b结尾的这些等差数列后面都加上一个c,这些新的等差数列也还是等差数列,加上a,b,c这个等差数列就是dp[i] = dp[i-1]+1】
两种情况最后三个数a,b,c根本无法构成等差数列,那么dp[i]=0
2.初始化:因为等差数列至少是三个数,那么dp[0] 和dp[1]根本无法构成等差数列,只能为0
3.根据dp表示可知,结果应该是dp表每个位置的和
class Solution {
public int numberOfArithmeticSlices(int[] nums) {
int n = nums.length;
int[] dp = new int[n];//dp[i]表示:以i位置为结尾的所有子数组中有多少个等差数列
int sum = 0;
for(int i=2;i<n;i++) {
dp[i] = nums[i]-nums[i-1]==nums[i-1]-nums[i-2]?dp[i-1]+1:0;
sum += dp[i];
}
return sum;
}
}二、最长湍流子数组
978. 最长湍流子数组

算法原理:

💡细节:
1.dp表的创建:如果只用一个dp表的话发现无法知道最后位置是上升还是下降,那么就考虑用两个dp表,一个表示子数组上升的最大长度,一个表示子数组下降的最大长度
2.初始化:根据状态转移方程,填表最差的情况都为1,那么直接全部初始化为1,那么有些填表的情况就不需要考虑了
3.返回值:两个表的最大值
💡总结:初始化的三种情况
(1)直接初始化会越界的位置
(2)加虚拟节点(但是有两个注意事项)=>初始化更简单
(3)把表中所有的位置都初始化为最小的情况(跟本题一样)
class Solution {
public int maxTurbulenceSize(int[] nums) {
int n = nums.length;
int[] f = new int[n];//上升
int[] g = new int[n];//下降
for(int i=0;i<n;i++) {
f[i] = g[i] = 1;
}
int ret = 1;
for(int i=1;i<n;i++) {
if(nums[i-1]<nums[i])
f[i] = g[i-1] + 1;
else if(nums[i-1]>nums[i])
g[i] = f[i-1] + 1;
ret = Math.max(ret,Math.max(g[i],f[i]));
}
return ret;
}
}三、单词拆分
139. 单词拆分

算法原理:
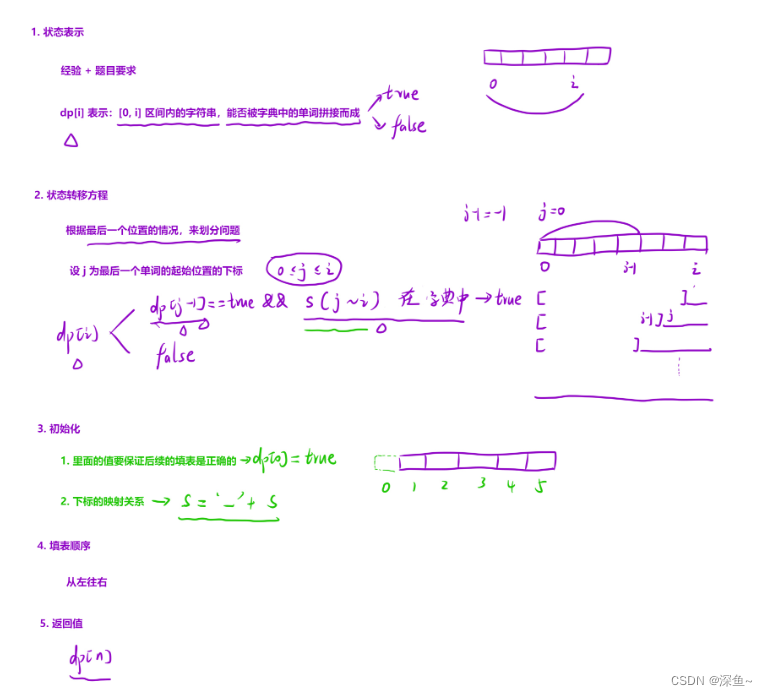
💡细节:
1.dp[i]:[0,i]区间内字符串是否可以被字典中的单词拼接而成,求状态转移方程时,需要设置最后一个单词的起始位置下标j,才能将dp进行联系,而且需要保证最后一个单词[j,i]在字典中&&上一个单词的位置dp[j-1]也为true
2.初始化:为了防止出现dp[j-1]中j-1为-1的情况,可以直接在s字符串前加一个字符,这样可以更好的处理下标的映射关系
3.优化1:找[j,i+1)的子串时,可以直接将字典中的单词存到哈希表中,在哈希表中去看子串是否存在
4.优化2:break =>只要在哈希表中找到一个单词即可,找到了就不用继续找下一个了
class Solution {
public boolean wordBreak(String s, List<String> wordDict) {
//优化1:将字典里面的单词存到哈希表中,在哈希表中找子串是否存在
Set<String> hash = new HashSet<>(wordDict);
int n = s.length();
boolean[] dp = new boolean[n+1];//dp[i]:0-i区间内的字符串能否被拼接成功
//初始化
dp[0] = true;
s = " " + s;//处理下标的映射关系(s的起始位置是从1开始的)
for(int i=1;i<=n;i++) {
for(int j=i;j>=1;j--) {
if(dp[j-1]==true && hash.contains(s.substring(j,i+1))) {//左闭右开
dp[i] = true;
break;//优化2:只要在哈希表中找到一个单词即可,找到了就不用继续找下一个了
}
}
}
return dp[n];
}
}四、环绕字符串中唯一的子字符串
467. 环绕字符串中唯一的子字符串

算法原理:

💡细节:
1.一般涉及子串的都会向长度为1,和长度大于1考虑状态转移方程
2.加一个连续字符的子串和未加这个字符的子串,当长度>1的时候,是一样大的,即dp[i]=dp[i-1]
3.初始化的技巧:直接初始化为最小值1,这样有些填表的情况就不需要考虑了
4.当个末尾字符相同的子串需要进行去重,创建一个大小为26的hash数组,把每个位置都填上以改字符结尾的最大dp值
class Solution {
public int findSubstringInWraproundString(String ss) {
int n = ss.length();
char[] s = ss.toCharArray();//转为数组好用下标
int[] dp = new int[n];//dp[i]:以i位置为结尾的所有子串里面,有多少个在base中出现过
for(int i=0;i<n;i++) dp[i] = 1;//全部初始化为最小值
for(int i=1;i<n;i++) {
if(s[i-1]+1==s[i]||(s[i-1]=='z'&&s[i]=='a'))
dp[i]+=dp[i-1];
}
//去重
int[] hash = new int[26];
for(int i=0;i<n;i++) {
hash[s[i]-'a'] = Math.max(dp[i],hash[s[i]-'a']);
}
int sum = 0;
for(int x:hash) sum+=x;
return sum;
}
}