LeetCode 112. 路径总和
1、题目
题目链接:112. 路径总和
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
叶子节点 是指没有子节点的节点。
示例 1:
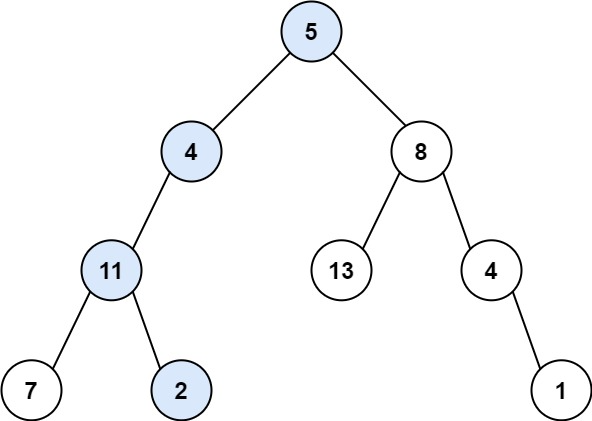
输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出:true
解释:等于目标和的根节点到叶节点路径如上图所示。
示例 2:
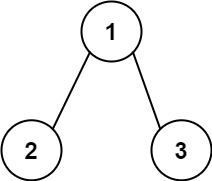
输入:root = [1,2,3], targetSum = 5
输出:false
解释:树中存在两条根节点到叶子节点的路径:
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。
示例 3:
输入:root = [], targetSum = 0
输出:false
解释:由于树是空的,所以不存在根节点到叶子节点的路径。
提示:
- 树中节点的数目在范围 [0, 5000] 内
- -1000 <= Node.val <= 1000
- -1000 <= targetSum <= 1000
2、深度优先搜索(递归)
思路
观察要求我们完成的函数,我们可以归纳出它的功能:询问是否存在从当前节点 root 到叶子节点的路径,满足其路径和为 targetSum。
假定从根节点到当前节点的值之和为 val,我们可以将这个大问题转化为一个小问题:是否存在从当前节点的子节点到叶子的路径,满足其路径和为 targetSum - val。
不难发现这满足递归的性质,若当前节点就是叶子节点,那么我们直接判断 targetSum 是否等于 val 即可(因为路径和已经确定,就是当前节点的值,我们只需要判断该路径和是否满足条件)。若当前节点不是叶子节点,我们只需要递归地询问它的子节点是否能满足条件即可。
代码
#include <iostream>
using namespace std;
//Definition for a binary tree node.
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
class Solution {
public:
bool traversal(TreeNode* root, int count) {
// 如果当前节点是叶子节点,并且count为0,则返回true
if (root->left == nullptr && root->right == nullptr && count == 0) {
return true;
}
// 如果当前节点是叶子节点,但count不为0,则返回false
if (root->left == nullptr && root->right == nullptr && count != 0) {
return false;
}
// 如果左子节点存在
if (root->left) {
// 将count减去左子节点的值
count -= root->left->val;
// 递归调用traversal函数处理左子树
if (traversal(root->left, count)) {
// 如果左子树返回true,则直接返回true
return true;
}
// 否则,回溯,恢复count的值,继续处理右子树
count += root->left->val;
}
// 如果右子节点存在
if (root->right) {
// 将count减去右子节点的值
count -= root->right->val;
// 递归调用traversal函数处理右子树
if (traversal(root->right, count)) {
// 如果右子树返回true,则直接返回true
return true;
}
// 否则,回溯,恢复count的值
count += root->right->val;
}
// 如果左子树和右子树都没有返回true,则返回false
return false;
}
bool hasPathSum(TreeNode* root, int targetSum) {
if (root == nullptr) {
return false;
}
return traversal(root, targetSum - root->val);
}
};
int main() {
Solution s;
TreeNode* root = new TreeNode(5);
root->left = new TreeNode(4);
root->right = new TreeNode(8);
root->left->left = new TreeNode(11);
root->left->left->left = new TreeNode(7);
root->left->left->right = new TreeNode(2);
root->right->left = new TreeNode(13);
root->right->right = new TreeNode(4);
root->right->right->left = new TreeNode(5);
root->right->right->right = new TreeNode(1);
cout << s.hasPathSum(root, 22) << endl;
return 0;
}
复杂度分析
- 时间复杂度:O(N),其中 N 是树的节点数。对每个节点访问一次。
- 空间复杂度:O(H),其中 H 是树的高度。空间复杂度主要取决于递归时栈空间的开销,最坏情况下,树呈现链状,空间复杂度为 O(N)。平均情况下树的高度与节点数的对数正相关,空间复杂度为 O(logN)。
3、深度优先搜索(递归精简版)
思路
代码
class Solution {
public:
bool hasPathSum(TreeNode* root, int targetSum) {
// 如果根节点为空,则返回false
if (!root) {
return false;
}
// 如果根节点没有左子节点和右子节点,并且当前节点的值等于目标值,则返回true
if (!root->left && !root->right && targetSum == root->val) {
return true;
}
// 递归地在左子树中查找是否存在路径和为targetSum - 当前节点值的路径
// 或者在右子树中查找是否存在路径和为targetSum - 当前节点值的路径
return hasPathSum(root->left, targetSum - root->val) || hasPathSum(root->right, targetSum - root->val);
}
};
复杂度分析
- 时间复杂度:O(N),其中 N 是树的节点数。对每个节点访问一次。
- 空间复杂度:O(H),其中 H 是树的高度。空间复杂度主要取决于递归时栈空间的开销,最坏情况下,树呈现链状,空间复杂度为 O(N)。平均情况下树的高度与节点数的对数正相关,空间复杂度为 O(logN)。
4、广度优先搜索
思路
我们可以想到使用广度优先搜索的方式,记录从根节点到当前节点的路径和,以防止重复计算。
这样我们使用两个队列,分别存储将要遍历的节点,以及根节点到这些节点的路径和即可。
代码
class Solution {
public:
bool hasPathSum(TreeNode *root, int sum) {
if (root == nullptr) {
return false;
}
// 使用队列存储节点和节点路径和
queue<TreeNode *> queNode;
queue<int> queVal;
queNode.push(root);
queVal.push(root->val);
while (!queNode.empty()) {
// 取出队列头部的节点和路径和
TreeNode *now = queNode.front();
int temp = queVal.front();
queNode.pop();
queVal.pop();
// 当前节点为叶子节点
if (now->left == nullptr && now->right == nullptr) {
// 当前路径和等于目标和
if (temp == sum) {
return true;
}
continue;
}
// 当前节点有左子节点
if (now->left != nullptr) {
queNode.push(now->left);
// 将左子节点的路径和加入队列
queVal.push(now->left->val + temp);
}
// 当前节点有右子节点
if (now->right != nullptr) {
queNode.push(now->right);
// 将右子节点的路径和加入队列
queVal.push(now->right->val + temp);
}
}
return false;
}
};
复杂度分析
- 时间复杂度:O(N),其中 N 是树的节点数。对每个节点访问一次。
- 空间复杂度:O(N),其中 N 是树的节点数。空间复杂度主要取决于队列的开销,队列中的元素个数不会超过树的节点数。
LeetCode 113. 路径总和ii
1、题目
题目链接:113. 路径总和 II
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
叶子节点 是指没有子节点的节点。
示例 1:
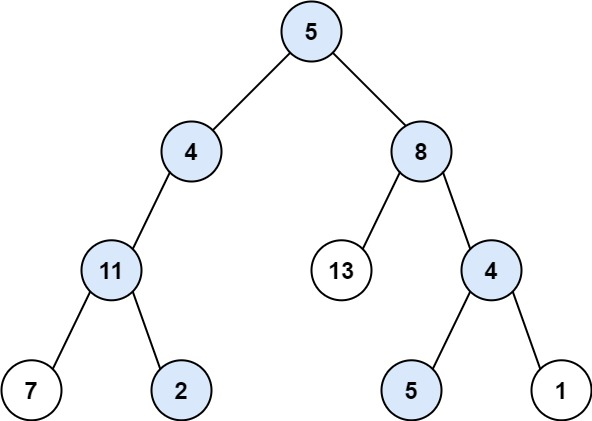
输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出:[[5,4,11,2],[5,8,4,5]]
示例 2:
输入:root = [1,2,3], targetSum = 5
输出:[]
示例 3:
输入:root = [1,2], targetSum = 0
输出:[]
提示:
- 树中节点总数在范围 [0, 5000] 内
- -1000 <= Node.val <= 1000
- -1000 <= targetSum <= 1000
2、深度优先搜索(递归)
思路
我们可以采用深度优先搜索的方式,枚举每一条从根节点到叶子节点的路径。当我们遍历到叶子节点,且此时路径和恰为目标和时,我们就找到了一条满足条件的路径。
代码
class solution {
private:
vector<vector<int>> result;
vector<int> path;
void traversal(TreeNode* cur, int count) {
// 如果当前节点为叶子节点且计数为0,则将路径加入结果集并返回
if (!cur->left && !cur->right && count == 0) {
result.push_back(path);
return;
}
// 如果当前节点为叶子节点,则直接返回
if (!cur->left && !cur->right) {
return;
}
// 如果当前节点有左子节点
if (cur->left) {
// 将左子节点的值加入路径
path.push_back(cur->left->val);
// 更新计数
count -= cur->left->val;
// 递归遍历左子节点
traversal(cur->left, count);
// 恢复计数
count += cur->left->val;
// 将左子节点的值从路径中移除
path.pop_back();
}
// 如果当前节点有右子节点
if (cur->right) {
// 将右子节点的值加入路径
path.push_back(cur->right->val);
// 更新计数
count -= cur->right->val;
// 递归遍历右子节点
traversal(cur->right, count);
// 恢复计数
count += cur->right->val;
// 将右子节点的值从路径中移除
path.pop_back();
}
return ;
}
public:
vector<vector<int>> pathSum(TreeNode* root, int sum) {
result.clear();
path.clear();
// 如果根节点为空,则直接返回空结果
if (root == nullptr) {
return result;
}
// 将根节点的值加入路径中
path.push_back(root->val);
// 调用遍历函数,传入当前节点和剩余的目标和
traversal(root, sum - root->val);
// 返回最终结果
return result;
}
};
复杂度分析
- 时间复杂度: O(n^2)
- 空间复杂度: O(n)
3、广度优先搜索
思路
我们也可以采用广度优先搜索的方式,遍历这棵树。当我们遍历到叶子节点,且此时路径和恰为目标和时,我们就找到了一条满足条件的路径。
为了节省空间,我们使用哈希表记录树中的每一个节点的父节点。每次找到一个满足条件的节点,我们就从该节点出发不断向父节点迭代,即可还原出从根节点到当前节点的路径。
代码
class Solution {
public:
vector<vector<int>> ret;
unordered_map<TreeNode*, TreeNode*> parent;
void getPath(TreeNode* node) {
// 创建一个临时向量,用于存储路径上的节点值
vector<int> tmp;
// 当节点不为空时,继续循环
while (node != nullptr) {
// 将当前节点的值添加到临时向量中
tmp.emplace_back(node->val);
// 将当前节点更新为其父节点
node = parent[node];
}
// 反转临时向量,使其按从根节点到叶子节点的顺序排列
reverse(tmp.begin(), tmp.end());
// 将反转后的路径添加到结果向量中
ret.emplace_back(tmp);
}
vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
if (root == nullptr) {
return ret;
}
// 使用队列进行广度优先搜索
queue<TreeNode*> que_node;
queue<int> que_sum;
que_node.emplace(root);
que_sum.emplace(0);
while (!que_node.empty()) {
TreeNode* node = que_node.front();
que_node.pop();
int rec = que_sum.front() + node->val;
que_sum.pop();
// 如果当前节点是叶子节点
if (node->left == nullptr && node->right == nullptr) {
// 如果路径和等于目标和
if (rec == targetSum) {
// 调用getPath函数获取路径
getPath(node);
}
} else {
// 如果左子节点不为空
if (node->left != nullptr) {
// 记录父节点
parent[node->left] = node;
// 将左子节点和路径和加入队列
que_node.emplace(node->left);
que_sum.emplace(rec);
}
// 如果右子节点不为空
if (node->right != nullptr) {
// 记录父节点
parent[node->right] = node;
// 将右子节点和路径和加入队列
que_node.emplace(node->right);
que_sum.emplace(rec);
}
}
}
return ret;
}
};
复杂度分析
- 时间复杂度: O(n^2)
- 空间复杂度: O(n)