机器学习算法应用——时间序列分析（4-5）

时间序列分析（4-5）

时间序列分析（Time-Series Analysis）是一种对按时间顺序排列的数据序列进行统计分析和预测的方法。这种方法通常用于研究某个现象随时间的变化规律，并据此预测未来的发展趋势。以下是时间序列分析的一些关键方面和常用方法（4-5点）：

关键方面：
- 动态性：时间序列数据是动态的，反映了某一现象随时间的变化过程。
- 规律性：时间序列数据往往包含一定的趋势、周期性和季节性等规律性特征。
- 预测性：通过对时间序列数据的分析，可以建立模型来预测未来的发展趋势。
常用方法：
- 趋势分析：确定时间序列数据的长期增长或下降趋势。这可以通过拟合线性或非线性模型来实现。
- 周期性和季节性分析：识别时间序列数据中的周期性或季节性模式。这有助于理解数据背后的周期性波动，如季节性的销售变化。
- 分解分析：将时间序列数据分解为趋势、周期、季节性和随机因素等组成部分。这有助于更深入地理解数据的结构。
- 时间序列预测：利用已有的时间序列数据来预测未来的值。这可以通过建立统计模型或使用机器学习算法来实现。例如，ARIMA模型、神经网络等都可以用于时间序列预测。
- 平稳性检验：检验时间序列数据是否具有平稳性。平稳性是指数据的统计特性（如均值、方差等）不随时间变化。平稳性检验是时间序列分析的一个重要步骤，因为许多时间序列模型都假设数据是平稳的。
应用：
- 系统描述：用时间序列数据对系统进行客观的描述。
- 系统分析：当观测值取自两个以上变量时，可以用一个时间序列中的变化去说明另一个时间序列中的变化。
- 预测未来：利用时间序列模型预测未来值，为决策提供支持。
- 决策和控制：根据时间序列模型调整输入变量，使系统发展过程保持在目标值上。

时间序列分析在金融、经济、气象、销售等多个领域都有广泛的应用。通过时间序列分析，我们可以更好地理解数据背后的规律，预测未来的发展趋势，并据此做出更明智的决策。

安装statsmodels库

pip install statsmodels

数据读取与预处理

使用pd.read_csv()读取并对日期数据进行转换

# 读取数据并进行预处理
data = """
"Month","Sales"
"1-01",266.0
"1-02",145.9
"1-03",183.1
"1-04",119.3
"1-05",180.3
"1-06",168.5
"1-07",231.8
"1-08",224.5
"1-09",192.8
"1-10",122.9
"1-11",336.5
"1-12",185.9
"2-01",194.3
"2-02",149.5
"2-03",210.1
"2-04",273.3
"2-05",191.4
"2-06",287.0
"2-07",226.0
"2-08",303.6
"2-09",289.9
"2-10",421.6
"2-11",264.5
"2-12",342.3
"3-01",339.7
"3-02",440.4
"3-03",315.9
"3-04",439.3
"3-05",401.3
"3-06",437.4
"3-07",575.5
"3-08",407.6
"3-09",682.0
"3-10",475.3
"3-11",581.3
"3-12",646.9
"""

# 将字符串转换为DataFrame
data = pd.read_csv(io.StringIO(data))

# 将'Month'列转换为日期类型
data['Month'] = pd.to_datetime(data['Month'], format='%m-%d')
# 将'Month'列转换为日期类型，并设置年份为2024年
data['Month'] = pd.to_datetime(data['Month'], format='%y-%m', yearfirst=True).dt.strftime('2024-%m')
print(data)
# 将日期列设置为索引
data.set_index('Month', inplace=True)

数据实例：

"Month","Sales"
"1-01",266.0
"1-02",145.9
"1-03",183.1
"1-04",119.3
"1-05",180.3
"1-06",168.5
"1-07",231.8
"1-08",224.5
"1-09",192.8
"1-10",122.9
"1-11",336.5
"1-12",185.9
"2-01",194.3
"2-02",149.5
"2-03",210.1
"2-04",273.3
"2-05",191.4
"2-06",287.0
"2-07",226.0
"2-08",303.6
"2-09",289.9
"2-10",421.6
"2-11",264.5
"2-12",342.3
"3-01",339.7
"3-02",440.4
"3-03",315.9
"3-04",439.3
"3-05",401.3
"3-06",437.4
"3-07",575.5
"3-08",407.6
"3-09",682.0
"3-10",475.3
"3-11",581.3
"3-12",646.9

检测序列的平稳性

时序图判断法

# 绘制时序图
data.plot(figsize=(10, 6))
plt.xlabel('Month')
plt.ylabel('Sales')
plt.title('Time Series of Sales')
plt.show()

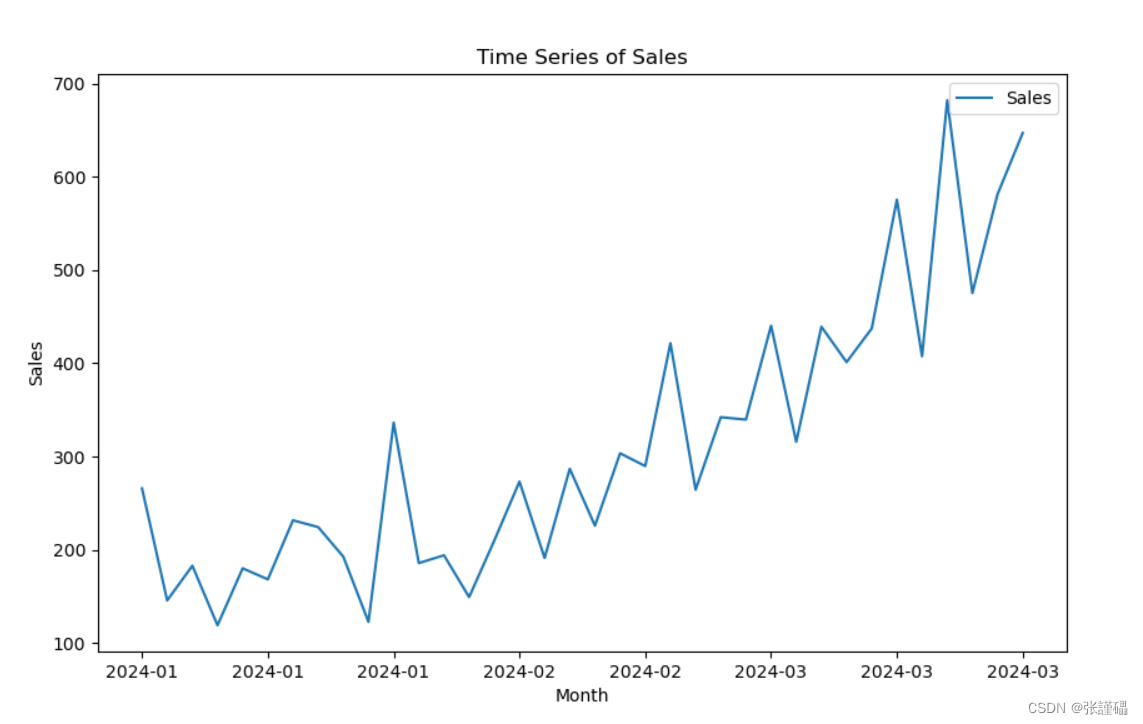
制自相关图判断法

# 检测序列的平稳性
# 自相关图
plot_acf(data, lags=9)
plt.title('Autocorrelation Plot')
plt.show()

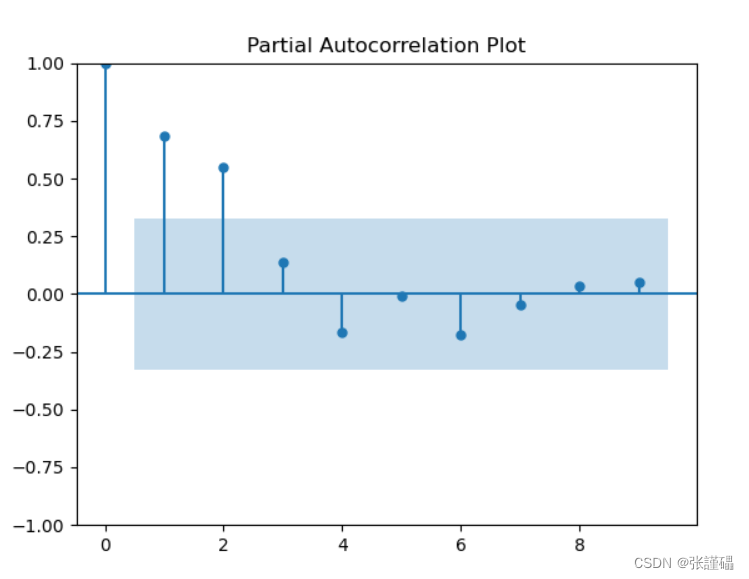
# 偏相关图
plot_pacf(data, lags=9)
plt.title('Partial Autocorrelation Plot')
plt.show()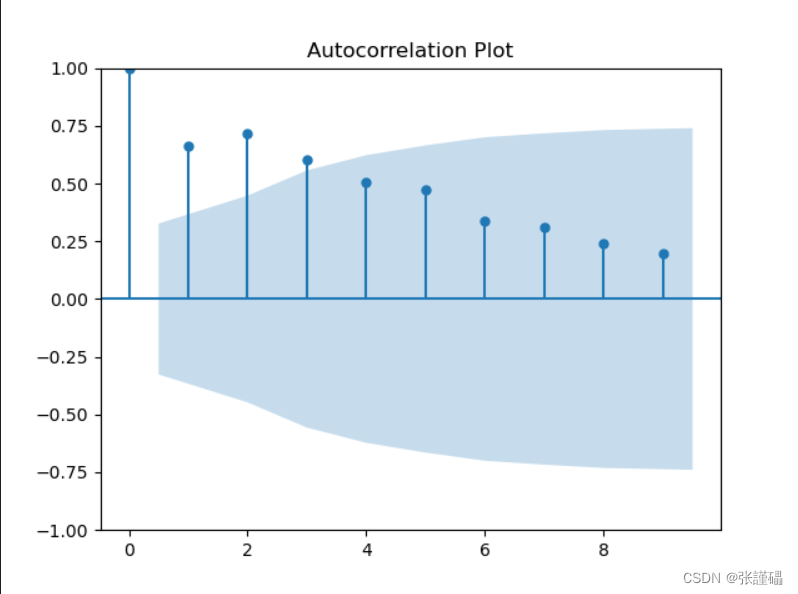

使用ADF单位根检测法

注意：p>0.05即为非平稳序列

# ADF检验
adf_result = adfuller(data['Sales'])
print('ADF Statistic:', adf_result[0])
print('p-value:', adf_result[1])
print('Critical Values:', adf_result[4])

差分处理

注意：根据上一步结果判断数据序列为非平稳序列，如想使用模型对数据进行建模，则需将数据转换为平稳序列。所以在这一步使用差分处理对序列进行处理。

# 差分处理
diff_data = data.diff().dropna()

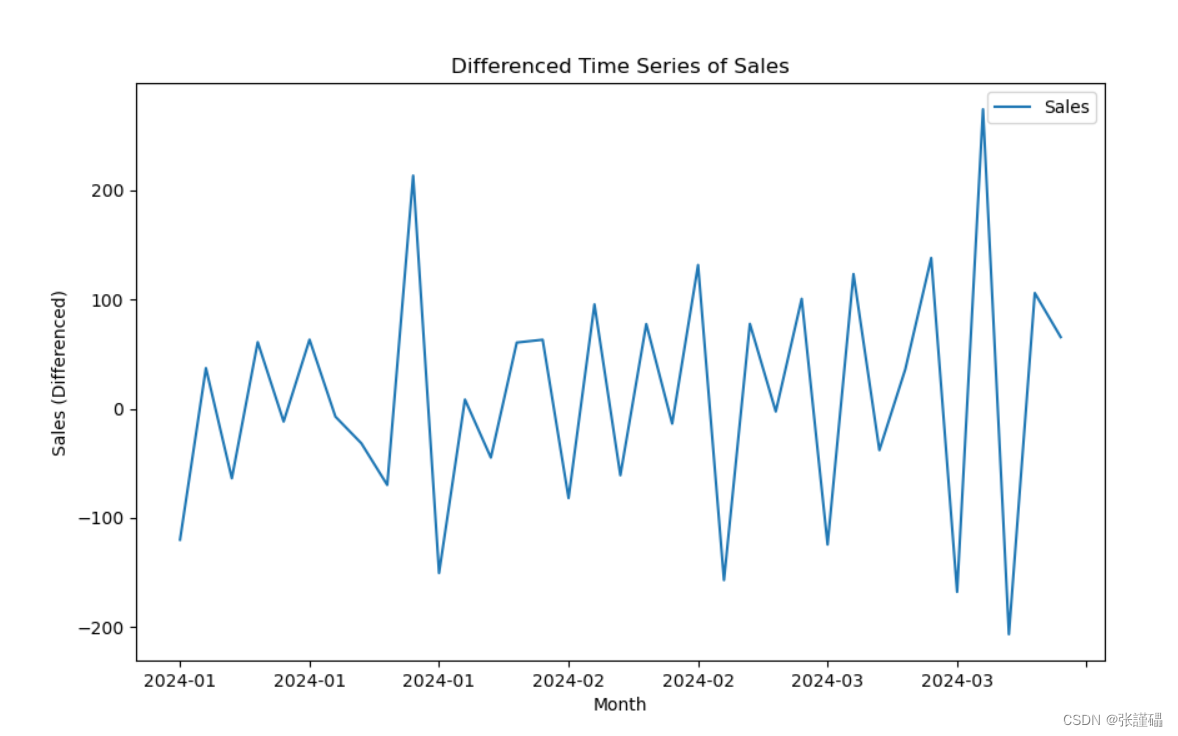
# 绘制差分后的时序图
diff_data.plot(figsize=(10, 6))
plt.xlabel('Month')
plt.ylabel('Sales (Differenced)')
plt.title('Differenced Time Series of Sales')
plt.show()

# 差分后的序列平稳性检测
# 自相关图
plot_acf(diff_data, lags=9)
plt.title('Autocorrelation Plot (Differenced)')
plt.show()

# 偏相关图
plot_pacf(diff_data, lags=9)
plt.title('Partial Autocorrelation Plot (Differenced)')
plt.show()

# ADF检验
adf_result_diff = adfuller(diff_data['Sales'])
print('ADF Statistic (Differenced):', adf_result_diff[0])
print('p-value (Differenced):', adf_result_diff[1])
print('Critical Values (Differenced):', adf_result_diff[4])

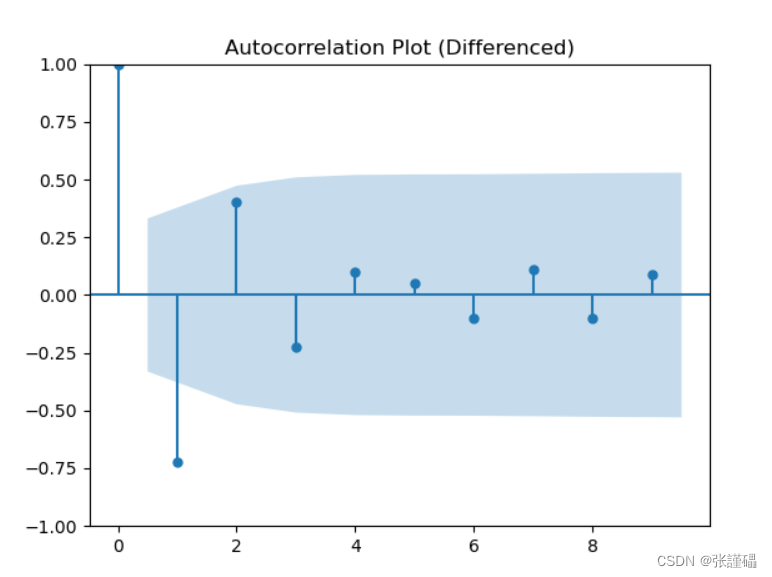
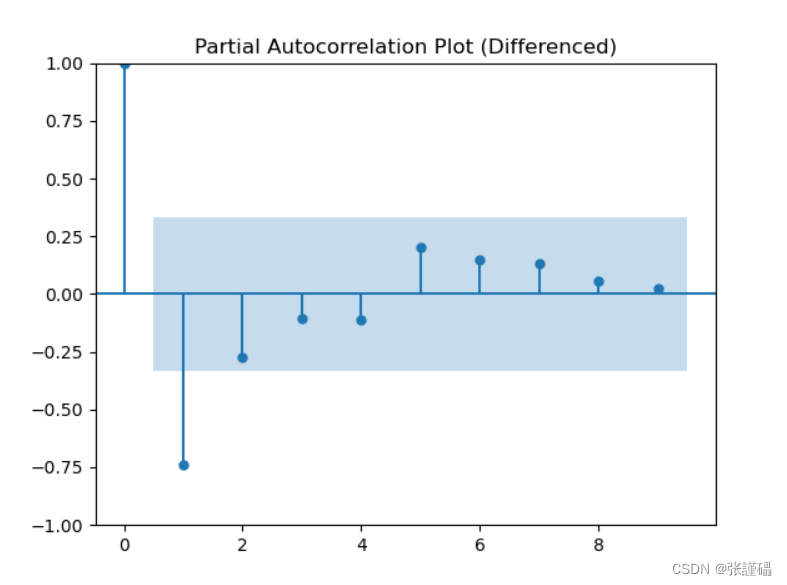
对处理后的序列进行平稳性检测（自相关图法、偏相关图法、ADF检测法）

使用ARIMA模型对差分处理后的序列进行建模

# 使用ARIMA模型建模
model = ARIMA(data, order=(1, 1, 1))
model_fit = model.fit()

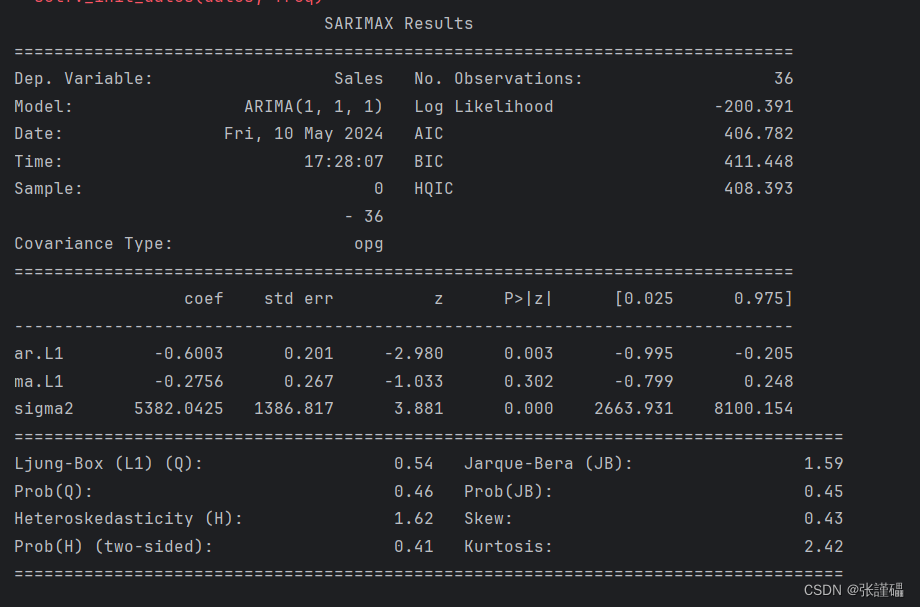
使用模型预测未来5个月的销售额

# 预测未来5个月的销售额
forecast_steps = 5
forecast = model_fit.forecast(steps=5)

完整代码：

import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import adfuller
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from statsmodels.tsa.arima.model import ARIMA
import io
# 读取数据并进行预处理
data = """
"Month","Sales"
"1-01",266.0
"1-02",145.9
"1-03",183.1
"1-04",119.3
"1-05",180.3
"1-06",168.5
"1-07",231.8
"1-08",224.5
"1-09",192.8
"1-10",122.9
"1-11",336.5
"1-12",185.9
"2-01",194.3
"2-02",149.5
"2-03",210.1
"2-04",273.3
"2-05",191.4
"2-06",287.0
"2-07",226.0
"2-08",303.6
"2-09",289.9
"2-10",421.6
"2-11",264.5
"2-12",342.3
"3-01",339.7
"3-02",440.4
"3-03",315.9
"3-04",439.3
"3-05",401.3
"3-06",437.4
"3-07",575.5
"3-08",407.6
"3-09",682.0
"3-10",475.3
"3-11",581.3
"3-12",646.9
"""

# 将字符串转换为DataFrame
data = pd.read_csv(io.StringIO(data))

# 将'Month'列转换为日期类型
data['Month'] = pd.to_datetime(data['Month'], format='%m-%d')
# 将'Month'列转换为日期类型，并设置年份为2024年
data['Month'] = pd.to_datetime(data['Month'], format='%y-%m', yearfirst=True).dt.strftime('2024-%m')
print(data)
# 将日期列设置为索引
data.set_index('Month', inplace=True)

# 绘制时序图
data.plot(figsize=(10, 6))
plt.xlabel('Month')
plt.ylabel('Sales')
plt.title('Time Series of Sales')
plt.show()

# 检测序列的平稳性
# 自相关图
plot_acf(data, lags=9)
plt.title('Autocorrelation Plot')
plt.show()

# 偏相关图
plot_pacf(data, lags=9)
plt.title('Partial Autocorrelation Plot')
plt.show()

# ADF检验
adf_result = adfuller(data['Sales'])
print('ADF Statistic:', adf_result[0])
print('p-value:', adf_result[1])
print('Critical Values:', adf_result[4])

# 差分处理
diff_data = data.diff().dropna()

# 绘制差分后的时序图
diff_data.plot(figsize=(10, 6))
plt.xlabel('Month')
plt.ylabel('Sales (Differenced)')
plt.title('Differenced Time Series of Sales')
plt.show()

# 差分后的序列平稳性检测
# 自相关图
plot_acf(diff_data, lags=9)
plt.title('Autocorrelation Plot (Differenced)')
plt.show()

# 偏相关图
plot_pacf(diff_data, lags=9)
plt.title('Partial Autocorrelation Plot (Differenced)')
plt.show()

# ADF检验
adf_result_diff = adfuller(diff_data['Sales'])
print('ADF Statistic (Differenced):', adf_result_diff[0])
print('p-value (Differenced):', adf_result_diff[1])
print('Critical Values (Differenced):', adf_result_diff[4])

# 使用ARIMA模型建模
model = ARIMA(data, order=(1, 1, 1))
model_fit = model.fit()

# 打印模型的概要信息
print(model_fit.summary())

# 预测未来5个月的销售额
forecast_steps = 5
forecast = model_fit.forecast(steps=5)
# 生成未来几个月的日期
last_month = data.index[-1]
future_months = pd.date_range(start=last_month, periods=forecast_steps + 1, freq='M')[1:]

# 创建包含日期和预测销售额的DataFrame
forecast_df = pd.DataFrame({'Month': future_months, 'Forecasted Sales': forecast})

# 输出预测结果
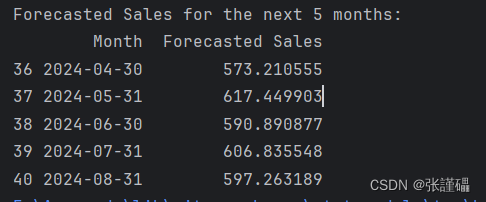
print('Forecasted Sales for the next 5 months:')
print(forecast_df)