文章目录
- 第一章 丰富的图形世界
- 1 生活中的立体图形
- 2 展开和折叠
- 3 截一个几何体
- 4 从三个方向看物体的形状
- 第二章 有理数及其运算
- 1 有理数
- 2 数轴
- 3 绝对值
- 4 有理数的加法
- 5 有理数的减法
- 6 有理数的加减混合运算
- 7 有理数的乘法
- 8 有理数的除法
- 9 有理数的乘方
- 10 科学计数法
- 11 有理数的混合运算
- 12 近似数
- 13 用计算器进行计算
- 第三章 整式及其加减
- 1 用字母表示数字
- 2 代数式
- 3 整式
- 4 合并同类型
- 5 去括号
- 6 整式的减法
- 7 探索与表达规律
- 第四章 一元一次方程
- 1 等式与方程
- 2 解一元一次方程
- 3 一元一次方程的应用
第一章 丰富的图形世界
1 生活中的立体图形
- 在棱柱中,相邻两个面的交线叫做棱,相邻两个侧面的交线叫做侧棱。棱柱的所有侧棱长都相等。棱柱的上、下底面的形状相同,侧面的形状都是平行四边形。
- 如果一个几何图形上的所有的点都在一个平面内,那么这样的几何图形是平面图形。如果一个几何图形上的点不都在一个平面上,那么这样的几何图形是立体几何。
2 展开和折叠

3 截一个几何体
- 用一个平面去截一个几何体,截出来的面叫做截面
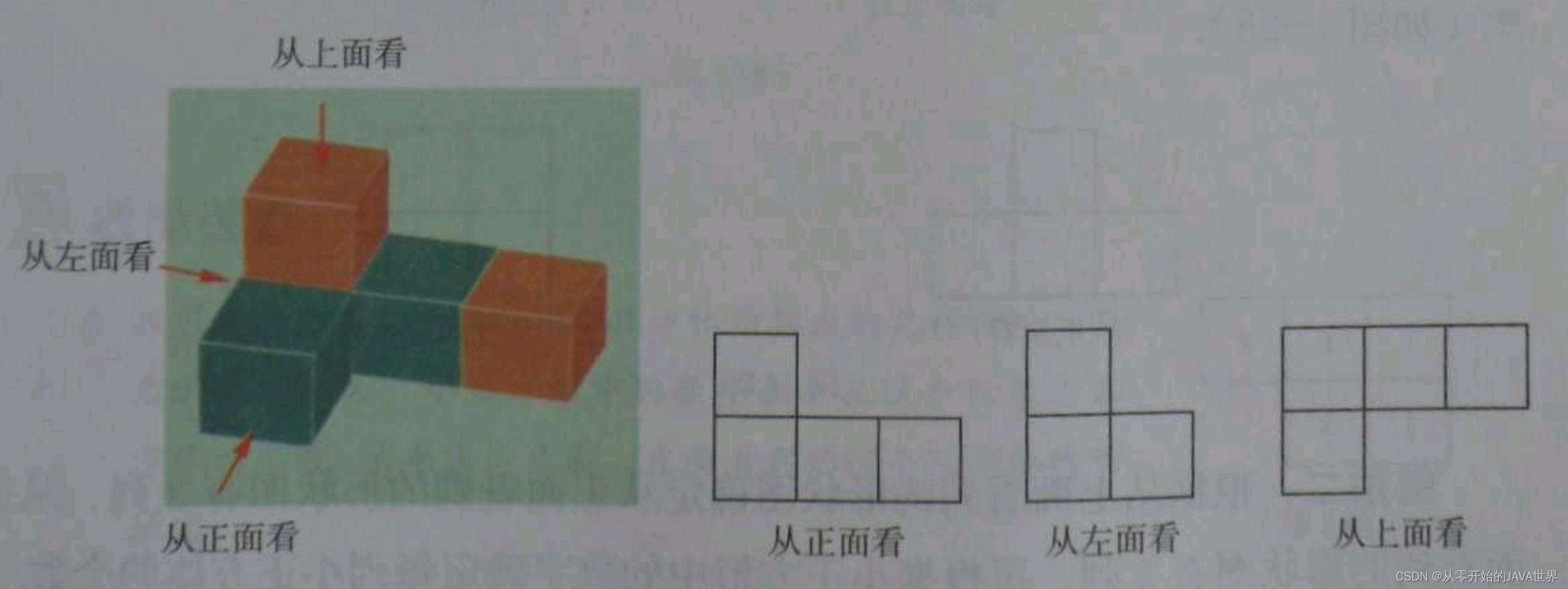
4 从三个方向看物体的形状
- 三视图
第二章 有理数及其运算
1 有理数
- 整数和分数统称为有理数。

2 数轴
- 画一条水平直线,在直线上取一点表示0,这个点叫做原点;选取某一长度作为单位长度;规定直线上向右的方向为正方向,就得到下面的数轴。
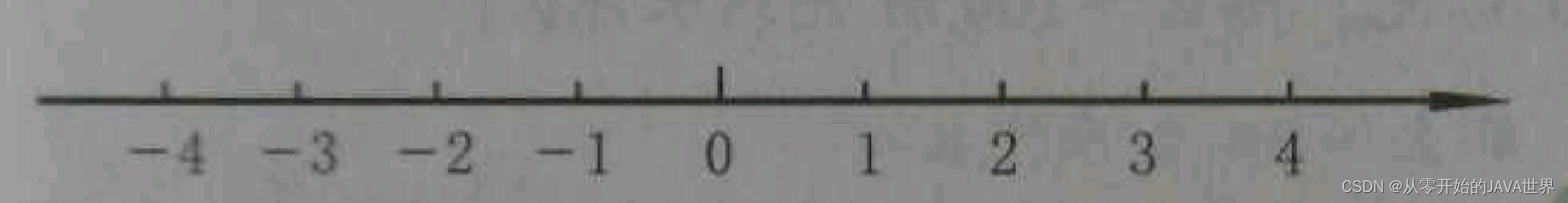
- 任何有理数都可以用数轴上的点来表示。
- 数轴上两个点表示的数,右边的总比左边的大。
- 正数大于0,负数小于0,正数大于负数。
3 绝对值
- 如果两个数只有符号不同,那么称其中一个数为另一个数的相反数,也称为这两个数互为相反数。特别地,0的相反数是0。
- 在数轴上,表示为互为相反数的两个点,位于原点的两侧,且与原点的距离相等。
- 在数轴上,一个数所对应的点与原点之间的距离叫做这个数的绝对值。例如,+2的绝对值等于2,记作|+2|=2;-3的绝对值等于3,记作|-3|=3。
- 正数的绝对值是它本身。
- 负数的绝对值是它的相反数。
- 0的绝对值是0。
- 两个负数比较大小,绝对值大的反而小。
4 有理数的加法
- 同号两数相加,取相同的符号,并把绝对值相加。
- 异号两数相加,绝对值相等时和为0;绝对值不相等时,取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值。
- 一个数同0相加,仍得这个数。
- 加法的交换律:a + b = b + a
- 加法的结合律:( a + b ) + c = a + ( b + c )
5 有理数的减法
- 有理数减法法则:减去一个数,等于加上这个数的相反数。
6 有理数的加减混合运算
7 有理数的乘法
- 有理数乘法法则:两数相乘,同号得正,异号得负,绝对值相乘。任何数与0相乘,积仍为0.
- 如果两个有理数的乘积为1,那么称其中的一个数是另一个数的倒数,也称这两个有理数互为倒数。
- 乘法的交换律:a·b = b·a
- 乘法的结合率:(a·b)·c = a·(b·c)
- 乘法对加法的分配率: a·(b + c) = a·b + a·c
8 有理数的除法
- 除以一个数等于乘这个数的倒数。
9 有理数的乘方

10 科学计数法
- 一般地,一个大于10的数可以表示称 a x 10^n 的形式,其中 1<= a <= 10,n是正整数,这种计数方法叫做科学计数法。
11 有理数的混合运算
- 先算乘方,再算乘除,最后算加减,如果有括号,先算括号里面的。
12 近似数
- 一般地,一个近似数四舍五入到哪一位,就说这个近似数精确到哪一位。
13 用计算器进行计算
第三章 整式及其加减
1 用字母表示数字
- 字母可以表示任何数
2 代数式

3 整式

- 几个单项式的和叫做多项式
- 在多项式中,每个单项式叫做多项式的项,不含字母的项叫做常数项。
- 单项式和多项式统称整式
4 合并同类型
- 字母相同,并且相同字母的指数也相同的项,叫做同类项,常数项都是同类项。
- 把同类项合并成一项,叫做合并同类项。
- 合并同类项时,把同类项的系数相加,字母和字母的指数不变。
- 合并同类项后的多项式,有几项就是几项试。次数最高的项的此时,叫做多项式的次数
5 去括号
- 括号前是+号,把括号和它前面的+号去掉后,原括号里各项的符号都不变。
- 括号前是-号,把括号和它前面的-号去掉后,原括号里各项的符号都要改变。
6 整式的减法
- 进行整式加减运算时,如果遇到括号要先去括号,再合并同类项。
7 探索与表达规律
第四章 一元一次方程
1 等式与方程
- 在一个方程中,只含有一个未知数,且未知数的指数都是1,这样的方程叫做一元一次方程。
- 使方程左、右两边都相等的未知数的值,叫做这个方程的解。
- 求方程的解的过程叫做解方程。
- 等式的基本性质1:等式两边同时加上(减去)同一个代数式,所得结果仍是等式。
- 等式的基本性质2:等式两边同时乘同一个数(或除以同一个不为0的数),所得结果仍是等式。
2 解一元一次方程
- 解一元一次方程,一般要通过去分母、去括号、移项、合并同类项、未知数的系数化为1等步骤,把一个一元一次方程转化乘 x = a的形式。