计算机组成与体系结构
- 计算机组成与体系结构
- 计算机结构 ★
- CPU 组成结构
- 运算器组成
- 控制器组成
- 计算机体系结构
- 冯诺依曼结构
- 哈弗结构
- 嵌入式芯片(了解)
- 存储系统 ★★★★
- 概述
- Cache
- 主存编址
- 磁盘管理
- 磁盘基本结构与存取过程
- 磁盘优化分布存储
- 磁盘管理
大家好呀!我是小笙,本章我主要分享系统架构设计师 - 计算机组成与体系结构(1)知识,这也是软考的第一篇文章,希望内容对你有所帮助!!
计算机组成与体系结构
计算机结构 ★
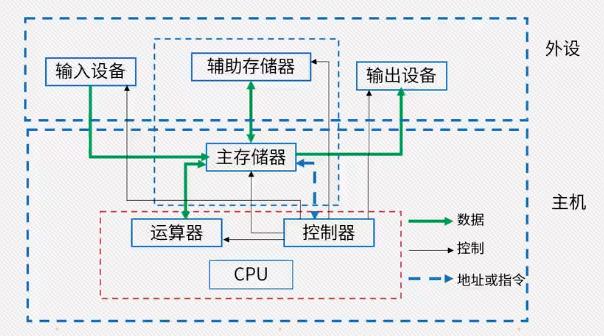
CPU 组成结构
运算器组成
- 算数逻辑单元 ALU:数据逻辑运算
- 数据缓冲寄存器 DR:读写内存
- 状态条件寄存器 PSW:溢出、进位标志
- 累加寄存器 AC:数据暂存区(通用寄存器)
控制器组成
- 程序计数器 PC:存储下一条要执行指令的地址
- 指令寄存器 IR:即将要执行的指令
- 指令译码器 ID:对指令的操作码字段进行分析解释
- 时序部件:提供时序控制信号
例题
计算机执行程序时,在一个指令周期的过程中,为了能够从内存中读指令操作
码,首先是将 程序计数器 PC 的内容送到地址总线上
计算机体系结构
冯诺依曼结构
称为普林顿结构,是一种程序指令和数据存储器合并在一起的存储结构
特点
- 指令和数据存储器合并在一起
- 指令和数据都通过相同的数据总线传输
- 一般用于PC 处理器 i3、i5、i7
哈弗结构
是一种特殊程序和数据存储分开的存储结构
特点
- 指令和数据分开存储,可以并行读取,有较高的数据吞吐率
- 有四条总线,指令与数据有各自的数据总线和地址总线
- 一般用于嵌入式系统处理器 DSP(数字信号处理)
例题
目前处理器市场中存在CPU和DSP两种类型处理器,分别用于不同场景,这两种处理器具有不同的体系结构,DSP采用 哈佛结构
- 冯·诺伊曼结构(一般用于PC 处理器 i3、i5、i7)
- 哈佛结构(一般用于嵌入式系统处理器 DSP)
- FPGA结构
- 与GPU相同结构
嵌入式芯片(了解)
| 定义 | 简称 | 特点 | 类比 | |
|---|---|---|---|---|
| DSP | DSP芯片,也称数字信号处理器,是一种特别适合于进行数字信号处理运算的微处理器,其主要应用是实时快速地实现各种数字信号处理算法 | 数字信号处理器 | 适合数字信号处理运算,实时快速地实现各种数组信号处理算法 | 做数学运算的“大脑 |
| SoC | 即片上系统。从狭义角度讲,它是信息系统核心的芯片集成,是将系统关键部件集成在一块芯片上;从广义角度讲,SoC是一个微小型系统,如果说中央处理器(CPU)是大脑,那么SoC就是包括大脑、心脏、眼睛和手的系统 | 片上系统 | 信息系统核心的芯片集成。微小型系统 | 包括大脑心脏、眼睛和手等、完成某个功能的系统 |
| MPU | 微机中的中央处理器(CPU)称为微处理器(MPU)是构成微机的核心部件,也可以说是微机的心脏。它起到控制整个微型计算机工作的作用,产生控制信号对相应的部件进行控制,并执行相应的操作 | 微处理器 | 微型机的核心部件,起到控制作用 | 缩小版“大脑“ |
| MCU | 微控制单元,又称单片微型计算机或者单片机,是把中央处理器(Central Process Unit;CPU)的频率与规格做适当缩减,并将内存(memory以、计数器(Timer)、USB、A/D转换、UART、PLC、DMA等周边接口,甚至LCD驱动电路都整合在单一芯片上,形成芯片级的计算机,为不同的应用场合做不同组合控制 | 单片微型计算机或单片机 | 芯片级计算机。对处理器做适当缩减,并将内存、计数器等周边接口整合在单一芯片上,可以为不同的应用场合做不同控制组合 | 缩小版“人” |
例题
嵌入式处理器是嵌入式系统的核心部件,一般可分为嵌入式微处理器(MPU)、微控制器(MCU)、数字信号处理器(DSP)和片上系统(SOC)。以下叙述中,错误的是MPU在安全性和可靠性等方面进行增强,适用于运算量较大的智能系统
- MPU在安全性和可靠性等方面进行增强,适用于运算量较大的智能系统(通过cpu卡板集成在芯片内部,利于嵌入式趋于小型化,具有效率性和可靠性,但是没有安全性)
- MCU典型代表是单片机,体积小从而使功耗和成本下降
- DSP处理器对系统结构和指令进行了特殊设计,适合数字信号处理
- SoC是一个有专用目标的集成电路,其中包括完整系统并有嵌入式软件的全部内容(指单个芯片集成完成系统)
存储系统 ★★★★
概述
从速度、容量以及价格三个性能指标来分析存储器
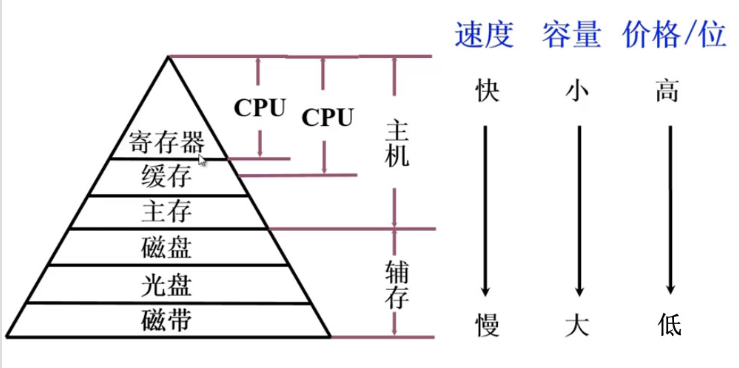
Cache
在计算机体系结构中,Cache 是访问速度最快的层次
目的:主要用于提高 CPU 数据输入输出的速率
为什么 Cache 能够快速的改善系统性能?
- 时间局部性原理:某条指令在某段时间内大量循环操作
- 空间局部性原理:访问了某个存储单元之后紧接着访问临近的存储地址顺序执行(遍历数组)
主存编址
- bit 比特位 0/1
- B 字节 1 B = 8bit
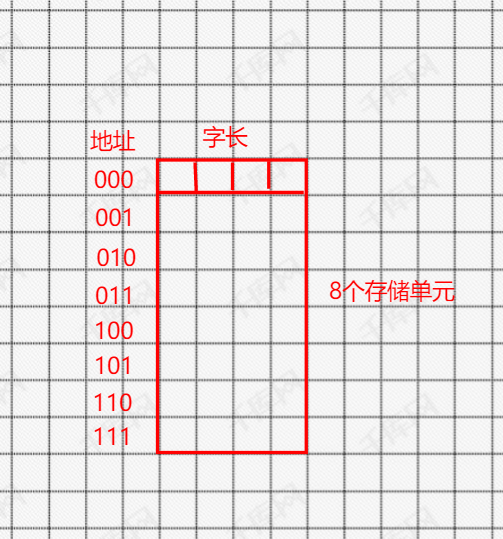
存储单元个数 = 最大地址 - 最小地址 + 1
按字编址和按字节编址的区别
- 按字编址:每个存储单元存储的内容(最小寻址单位就是一个字节)
- 按字节编址:每个存储单元的存储字大小固定为 8bit
总容量 = 存储单元个数 * 编址内容(字或者字节)
总片数 = 总容量 / 每片的容量
磁盘管理
磁盘基本结构与存取过程
磁盘
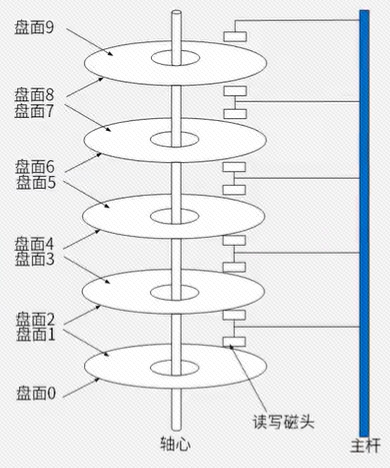
扇面
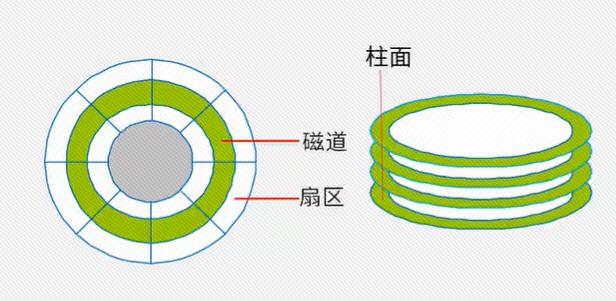
存取时间 = 寻道时间 + 等待时间,寻道时间是指磁头移动到磁道所需的时间;等待时间为等待读写的扇区转到磁头下方所用的时间
磁盘优化分布存储
磁盘管理
-
先来先服务(FCFS)
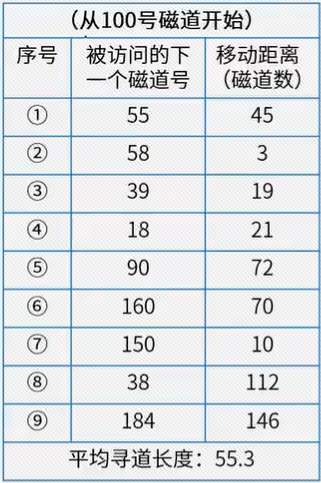
-
最短民道时间优先(SSTF)
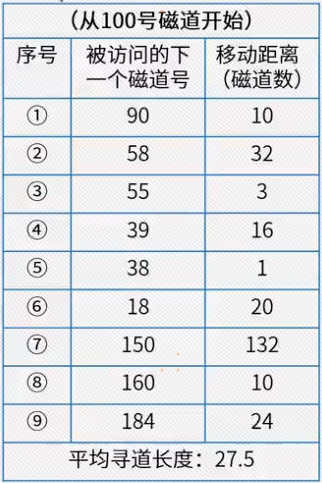
-
扫描算法(SCAN)
-
循环扫描算法(CSCAN)
例题
-
计算机采用分级存储体系的主要目的是为了 解决存储的容量、价格和速度之间的矛盾
- 解决主存容量不足的问题
- 提高存储器读写可靠性
- 提高外设访问效率
- 解决存储的容量、价格和速度之间的矛盾
-
h 表示 Cache 命中率,t1 表示 Cache 存储周期,t2表示主存的存储周期,求 Cache + 主存平均存储周期 t3
t3 = h * t1 + (1-h) * t2(命中则计算访问 Cache 的存储时间,不命中则是计算主存的存储时间)
-
内存按字节编址,利用 8K * 4bit 的存储芯片构成 84000 H 到 8FFFF H 的内存,共需要多少片数?
- 存储单元个数 = 8FFFF H + 1 - 84000 H = 12 * 16^3
- 按字节编址 8 bit
- 总容量 = 存储单元个数 * 编址内容 = 12 * 16^3 * 8 bit
- 每片容量 = 8K * 4bit = 8 * 1024 * 4 bit
- 总片数 = 总容量 / 每片的容量 = 12 * 16^3 * 8 bit / 8 * 1024 * 4 bit = 12个
-
某磁盘磁头从一个磁道移至另一个磁道需要10ms。文件在磁盘上非连续存放,逻辑上相邻数据块的平均移动距离为10个磁道,每块的旋转延迟时间及传输时间分别为100ms和2ms,则读取一个100块的文件需要 20200 ms时间
说明:(10 * 10 + 100 + 2)* 100 = 20200 ms
- 10200
- 11000
- 11200
- 20200
-
假设磁盘臂位于15号柱面上,进程的请求序列如下表表示,如果采用最短移臂调度算法,那么系统的响应序列应为 ⑤①②④③⑥
A:①②③④⑤⑥
B:⑤①②④③⑥
C:②③④⑤①⑥
D:④②③⑤①⑥