计算图与自动微分
- 一、自动梯度计算
- 1.1 数值微分(Numerical Differentiation)
- 1.2 符号微分(Symbolic Differentiation)
- 1.3 自动微分(Automatic Differentiation,AD)
- 1.3.1 计算图
- 1.3.2 正向传播
- 1.3.3 反向传播
- 1.3.4 计算图构建方式
一、自动梯度计算
自动计算梯度的方法可以分为以下三类:数值微分、符号微分和自动微分。
1.1 数值微分(Numerical Differentiation)
数值微分使用数值的方法来计算函数
f
(
x
)
f(x)
f(x)的导数,函数
f
(
x
)
f(x)
f(x)的导数定义为:
f
′
(
x
)
=
lim
Δ
x
→
0
f
(
x
+
Δ
x
)
−
f
(
x
)
Δ
x
f^\prime(x)=\lim_{\Delta x \rightarrow 0} \frac{f(x+\Delta x) - f(x)}{\Delta x}
f′(x)=Δx→0limΔxf(x+Δx)−f(x)
要计算函数 𝑓(𝑥) 在点 𝑥 的导数,可以对 𝑥 加上一个很少的非零的扰动 Δ𝑥,通过上述定义来直接计算函数𝑓(𝑥)的梯度。如在编程中令
Δ
x
=
0.0001
\Delta x=0.0001
Δx=0.0001。
数值微分方法非常容易实现,但
- 很难找到一个合适的扰动Δ𝑥 ,若 Δ x \Delta x Δx过小,会有舍入误差;若过大,会增加截断误差。因此数值微分实用性不大。
- 计算复杂度高,如果有N个参数,则每个参数都需要单独施加扰动,则计算数值微分的复杂度为 O ( N 2 ) O(N^2) O(N2)
1.2 符号微分(Symbolic Differentiation)
符号微分是一种基于符号计算的自动求导方法,符号计算也叫代数计算,是指用计算机处理处理带有变量的数学表达式,这里的变量被看作符号(symbols),一般不需要代入具体的值。符号计算的输入和输出都是书数学表达式,一般包括对数学表达式的化简、因式分解、微分、积分、解代数方程、求解常微分方程等运算。
使用Python中sympy库求函数导数:
import sympy
x = sympy.symbols('x')
func = x ** 2
func_derivative = sympy.diff(func)
print(func_derivative)
2*x
符号微分可以在编译时就计算梯度的数学表示,并进一步利用符号计算方
法进行优化.此外,符号计算的一个优点是符号计算和平台无关,可以在CPU或GPU 上运行.符号微分也有一些不足之处:
- 1)编译时间较长,特别是对于循环,需要很长时间进行编译;
- 2)为了进行符号微分,一般需要设计一种专门的语言来表示数学表达式,并且要对变量(符号)进行预先声明;
- 3)很难对程序进行调试
1.3 自动微分(Automatic Differentiation,AD)
自动微分是一种可以对一个函数进行计算导数的方法,其基本原理是所有的数值计算可以分解为一些基本操作,包含±*/,和一些初等函数exp,log,sin,cos等(可以用计算图表示),然后利用链式法则来自动计算一个复合函数的梯度。
以函数
f
(
x
;
w
,
b
)
f(x;w,b)
f(x;w,b)为例,其中x为变量,w和b为参数。
f
(
x
;
w
,
b
)
=
1
e
−
(
w
x
+
b
)
+
1
f(x;w,b)=\frac{1}{\text{e}^{-(wx+b)}+1}
f(x;w,b)=e−(wx+b)+11
1.3.1 计算图
计算图是数学运算的图形化表示.计算图中的每个非叶子节点表示一个基本操作,每个叶子节点为一个输入变量或常量。因此,将复合函数
f
(
x
;
w
,
b
)
f(x;w,b)
f(x;w,b)分解为一系列的基本操作,构成一个计算图,当x=1,w=0,b=0时,
f
(
x
;
w
,
b
)
f(x;w,b)
f(x;w,b)的计算图如图所示。
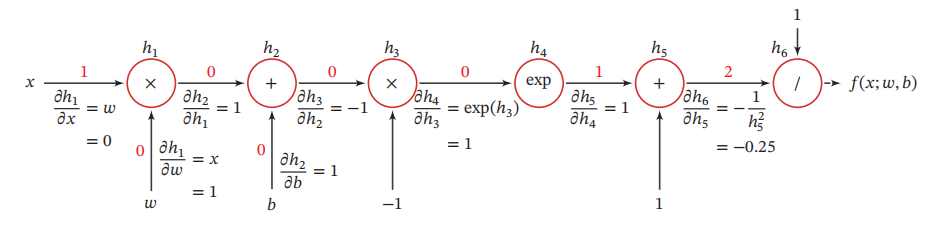
其中红色数字代表变量实际取值。
1.3.2 正向传播
正向传播(forward propagation)是指对神经⽹络沿着从输⼊层到输出层的顺序,依次计算并存储模型的中间变量(包括输出),即对输入计算模型输出。
正向传播输入x=1,w=0,b=0,输出 f ( 1 ; 0 , 0 ) = 0.5 f(1;0,0)=0.5 f(1;0,0)=0.5
1.3.3 反向传播
反向传播(back-propagation)指的是计算神经⽹络参数梯度的⽅法。总的来说,反向传播依据
微积分中的链式法则,沿着从输出层到输⼊层的顺序,依次计算并存储⽬标函数有关神经⽹络各层的中间变量以及参数的梯度
从计算图可以看出,复合函数 f ( x ; w , b ) f(x;w,b) f(x;w,b)由6个基本函数 h i , 1 ≤ i ≤ 6 h_i, 1 \leq i \leq 6 hi,1≤i≤6组成。如下表所示,每个基本函数的导数都十分简单,可以通过规则来实现。

整个复合函数
f
(
x
;
w
,
b
)
f(x;w,b)
f(x;w,b)关于参数
w
w
w和
b
b
b的导数可以通过计算图上的节点
f
(
x
;
w
,
b
)
f(x;w,b)
f(x;w,b)与参数
w
w
w和
b
b
b之间路径上所有的导数连乘得到,即
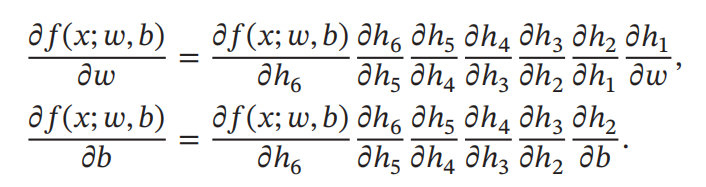
∂
f
(
x
;
w
,
b
)
∂
w
=
∂
f
(
x
;
w
,
b
)
∂
h
6
∂
h
6
∂
h
5
∂
h
5
∂
h
4
∂
h
4
∂
h
3
∂
h
3
∂
h
2
∂
h
2
∂
h
1
∂
h
1
∂
w
=
1
×
−
1
h
5
2
×
1
×
e
h
3
×
−
1
×
1
×
x
=
0.25
\begin{align} \frac{\partial f(x;w,b)}{\partial w} &=\frac{\partial f(x;w,b)}{\partial h_6} \frac{ \partial h_6}{\partial h_5} \frac{\partial h_5}{\partial h_4} \frac{\partial h_4}{\partial h_3} \frac{\partial h_3}{\partial h_2} \frac{\partial h_2}{\partial h_1} \frac{\partial h_1}{\partial w} \\ &=1 \times -\frac{1}{h_5^2} \times 1 \times \text{e}^{h_3} \times-1 \times 1 \times x\\ &= 0.25 \end{align}
∂w∂f(x;w,b)=∂h6∂f(x;w,b)∂h5∂h6∂h4∂h5∂h3∂h4∂h2∂h3∂h1∂h2∂w∂h1=1×−h521×1×eh3×−1×1×x=0.25
如果函数和参数之间有多条路径,可以将这多条路径上的导数再进行相加,得到最终的梯度.
1.3.4 计算图构建方式
计算图按构建方式可以分为
- 动态计算图:在程序运行时动态构建,不容易优化,当不同输入的网络结构不一致时,难以并行计算,但是灵活性比较高.
- 静态计算图:在编译时构建计算图,计算图构建好之后在程序运行时不能改变,在构建时可以进行优化,并行能力强,但灵活性比较差.
参考:
- https://www.bilibili.com/video/BV1PF411h7Ew/?spm_id_from=333.337.search-card.all.click&vd_source=52f9eb63aa834f8c039c3dedc7463736
- 《动手学深度学习》
- 《神经网络与深度学习》
- 《深度学习入门—基于Python的理论与实现》