最后一块石头重量Ⅱ

有一堆石头，每块石头的重量都是正整数。

每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：

如果 x == y，那么两块石头都会被完全粉碎；

如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。

最后，最多只会剩下一块石头。返回此石头最小的可能重量。如果没有石头剩下，就返回 0。

示例：

• 输入：[2,7,4,1,8,1]
• 输出：1

解释：

• 组合 2 和 4，得到 2，所以数组转化为 [2,7,1,8,1]，
• 组合 7 和 8，得到 1，所以数组转化为 [2,1,1,1]，
• 组合 2 和 1，得到 1，所以数组转化为 [1,1,1]，
• 组合 1 和 1，得到 0，所以数组转化为 [1]，这就是最优值。

提示：

• 1 <= stones.length <= 30
• 1 <= stones[i] <= 1000

​ 关键点在想到：让石头尽量分成重量相同的两堆，相撞之后剩下的石头最小；

​ 又因为唯一性，很自然就化解为了01背包问题；

​ 本题物品的重量为stones[i]，物品的价值也为stones[i]。

​ 对应着01背包里的物品重量weight[i]和 物品价值value[i]。

​ 动规五部曲：
​ 1.dp数组含义：
​ dp[j]表示容量为j的背包，最多可以背的最大重量为dp[j]；

​ 2.确定递推公式：

​ dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);

​ 3.初始化：

​ 因为提示中给出1 <= stones.length <= 30，1 <= stones[i] <= 1000，所以最大重量就是30 * 1000 。

​ 而我们要求的target其实只是最大重量的一半，所以dp数组开到15000大小就可以了。

​ 当然也可以把石头遍历一遍，计算出石头总重量 然后除2，得到dp数组的大小。

​ 我这里就直接用15000了。

​ 即vector<int> dp (15001, 0);

​ 4.遍历顺序：

​ 和之前的一致，内层倒序：

for (int i = 0; i < stones.size(); i++) { // 遍历物品
    for (int j = target; j >= stones[i]; j--) { // 遍历背包
        dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
    }
}

​ 5.打印数组：

#include<iostream>
#include<vector>
#include<numeric>
using namespace std;
class solution {
public:
	int lastStoneWeightII(vector<int>& stones){
		int sum = accumulate(stones.begin(), stones.end(), 0);//向下取整求背包的最大空间
		int target = sum / 2;
		vector<int> dp(15001, 0);//根据测试案例调整dp数组大小
		for (int i = 0; i < stones.size(); i++) {
			cout << "The current dp array is:" << endl;
			for (int j = target; j >= stones[i]; j--) {
				dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
			}
			for (int k = 0; k <= target; k++) {
				cout << dp[k] << ' ';
			}
			cout << endl;
		}
		return sum - 2 * dp[target];
	}
};
int main() {
	solution mySolution;
	vector<int> tests = { 2,4,1,1 };
	cout << "The result is:" << mySolution.lastStoneWeightII(tests) << endl;
	return 0;
}

目标和

给定一个非负整数数组，a1, a2, …, an, 和一个目标数，S。现在你有两个符号 + 和 -。对于数组中的任意一个整数，你都可以从 + 或 -中选择一个符号添加在前面。

返回可以使最终数组和为目标数 S 的所有添加符号的方法数。

示例：

• 输入：nums: [1, 1, 1, 1, 1], S: 3
• 输出：5

解释：

• -1+1+1+1+1 = 3
• +1-1+1+1+1 = 3
• +1+1-1+1+1 = 3
• +1+1+1-1+1 = 3
• +1+1+1+1-1 = 3

一共有5种方法让最终目标和为3。

提示：

• 数组非空，且长度不会超过 20 。
• 初始的数组的和不会超过 1000 。
• 保证返回的最终结果能被 32 位整数存下。

​ 先不考虑是否为背包问题，先分析问题本身；其实还是可以视为一个子集划分的问题;

​ 由于数组非负，所以target = sum_plus - sum_minus其中，sum_plus + sum_minus = sum；

​ 所以sum_minus = (sum - target)/2;

​ 找这个sum_minus是否存在即可

​ 动规五部曲：

​ 1.dp数组及其下标含义：

​ dp[j]表示sum_minus为j时有dp[j]种方法使得子集和为sum_minus;

​ 2.确认递推公式：

​ 这里借用二维数组来方便理解：

​ dp[i][j] = dp[i-1][j] + dp[i-1][j -nums[i]];

​ dp[i - 1][j]是不将物品i放入背包的方式数，dp[i-1][j - nums[i]]使将物品i放入背包的方式数；

​ 再次确定此时一维dp数组含义，dp[j]指的是子集和为j的情况下的路径数：

​ 要用若干个元素组成和为j的方案数，那么有两种选择：不选第i个元素或者选第i个元素；

​ 如果不选第i个元素，那么原来已经有多少种方案数就不变；

​ 如果选第i个元素，那么就是在已有的基础上，加上剩下要组成和为j - nums[i] 的方案数就等于dp[j - nums[i]];

​ 所以，很显然，dp[j] = dp[j] + dp[j - nums[i]];

​ 3.初始化：

​ 很显然，根据上面的推导，dp[0] = 1，不然的话所有项都是0，其余dp[j] = 0;

​ 4.遍历顺序：

​ 经典一维01背包

​ 5.打印数组：
​

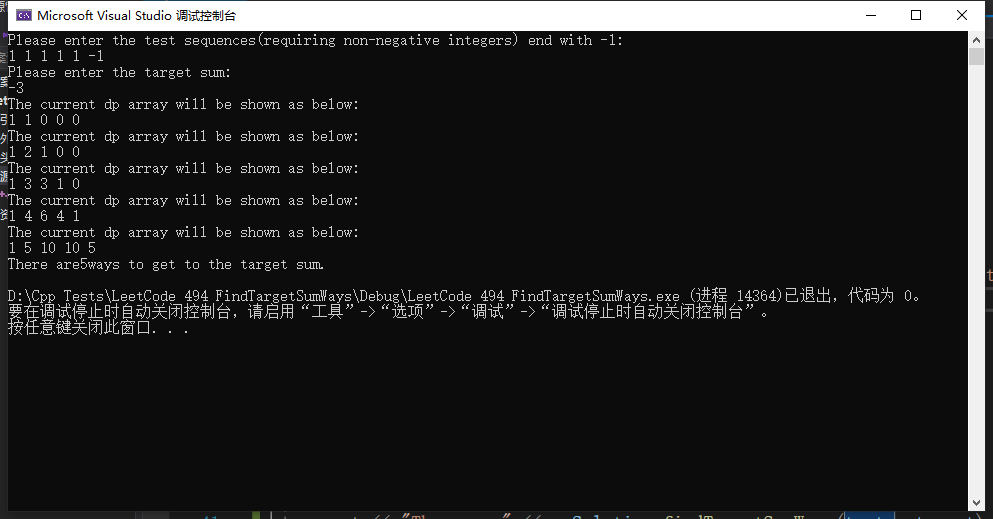
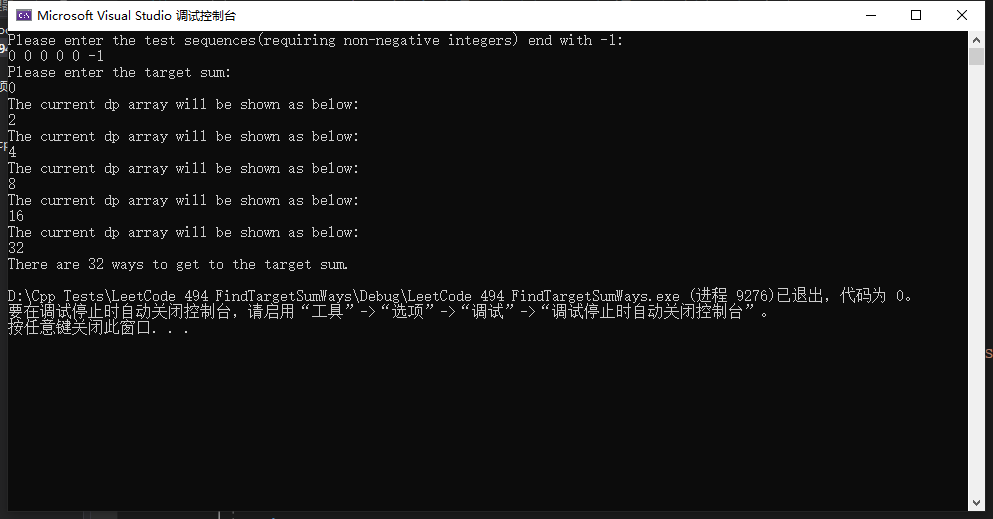
#include<numeric>
#include<iostream>
#include<vector>

using namespace std;

class solution {
public:
	int findTargetSumWays(vector<int>& nums, int target) {
		int sum = accumulate(nums.begin(), nums.end(), 0);
		if (abs(target) > sum)	return 0;
		if ((sum -  target) % 2 == 1)	return 0;
		int sum_minus = (sum - target) / 2;
		vector<int> dp(1001, 0);//因为初始数组和小于1000，target可取范围为-1000-1000，所以sum_minus <= 1000恒成立
		dp[0] = 1;
		for (int i = 0; i < nums.size(); i++) {
			for (int j = sum_minus; j >= nums[i]; j--) {
				dp[j] += dp[j - nums[i]];
			}
			cout << "The current dp array will be shown as below:" << endl;
			for (int k = 0; k <= sum_minus; k++) {
				cout << dp[k] << ' ';
			}
			cout << endl;
		}
		return dp[sum_minus];
	}
};

int main() {
	cout << "Please enter the test sequences(requiring non-negative integers) end with -1:" << endl;
	vector<int> tests;
	int num;
	while (cin >> num && num != -1) {
		tests.push_back(num); // 将输入的整数添加到vector中  
	}
	cout << "Please enter the target sum:" << endl;
	int target;
	cin >> target;
	solution mySolution;
	cout << "There are " << mySolution.findTargetSumWays(tests, target) << " ways to get to the target sum." << endl;
	return 0;
}

一和零

给你一个二进制字符串数组 strs 和两个整数 m 和 n 。

请你找出并返回 strs 的最大子集的大小，该子集中 最多 有 m 个 0 和 n 个 1 。

如果 x 的所有元素也是 y 的元素，集合 x 是集合 y 的 子集 。

示例 1：

• 输入：strs = [“10”, “0001”, “111001”, “1”, “0”], m = 5, n = 3
• 输出：4
• 解释：最多有 5 个 0 和 3 个 1 的最大子集是 {“10”,“0001”,“1”,“0”} ，因此答案是 4 。 其他满足题意但较小的子集包括 {“0001”,“1”} 和 {“10”,“1”,“0”} 。{“111001”} 不满足题意，因为它含 4 个 1 ，大于 n 的值 3 。

示例 2：

• 输入：strs = [“10”, “0”, “1”], m = 1, n = 1
• 输出：2
• 解释：最大的子集是 {“0”, “1”} ，所以答案是 2 。

提示：

• 1 <= strs.length <= 600
• 1 <= strs[i].length <= 100
• strs[i] 仅由 ‘0’ 和 ‘1’ 组成
• 1 <= m, n <= 100

​ 看起来好像很复杂，实际上就是拥有两个维度的背包，容量分别为m和n；

​ 至于strs虽然看上去有许多重复的0 1，但是实际上每个strs[i]只能取一次，所以还是0-1背包问题；

​ 动规五部曲：
​ 1.dp数组含义及其下标：

​ dp[i][j]，表示在子集在最多有m个0，n个1的前提下，最多可以选择有dp[i][j]个元素；

​ 2.递推公式：

​ 先考虑最原始的0-1背包问题:

​ dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + values[i]);

​ 对于本题：

​ dp[i][j] = max(dp[i][j], dp[i - zero_nums][y - one_nums] +1);

​ 3.初始化：
​ 很显然，此时的dp[0][0] = 0;

​ 又因为递推公式是需要比较最大值的，所以所有dp[i][j] = 0;

​ 4.遍历顺序：

​ 经典倒序：

		for (string str : strs) { // 遍历物品
            int oneNum = 0, zeroNum = 0;
            for (char c : str) {
                if (c == '0') zeroNum++;
                else oneNum++;
            }
            for (int i = m; i >= zeroNum; i--) { // 遍历背包容量且从后向前遍历！
                for (int j = n; j >= oneNum; j--) {
                    dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
                }
            }
        }

​ 5.打印dp数组：

#include<iostream>
#include<string>
#include<vector>
using namespace std;
class solution {
public:
	int findMaxFormvector(vector<string>& strs, int m, int n) {
		vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));//dp数组初始化
		for (vector<string>::size_type i = 0; i < strs.size(); i++) {
			string str = strs[i];
			int zero_nums = 0, one_nums = 0;
			for (string::size_type j = 0; j < str.size(); j++) {
				char c = str[j];
				if (c == '1')	one_nums++;
				else zero_nums++;
			}
			for (int i = m; i >= zero_nums; i--) {
				for (int j = n; j >= one_nums; j--) {
					dp[i][j] = max(dp[i][j], dp[i - zero_nums][j - one_nums] + 1);
				}
			}
			cout << "The current dp array will be shown as below:" << endl;
			for (int i = 0; i <= m; i++) {
				for (int j = 0; j <= n; j++) {
					cout << dp[i][j] << ' ';
				}
				cout << endl;
			}
		}
		return dp[m][n];
	}
};

int main() {
	cout << "Please enter the strings(only 0 and 1 are allowed),seperated by enter,quit with\"stop\"" << endl;
	solution ms;
	vector<string> strs;
	string input;
	while (true) {
		getline(cin, input);
		if (input == "stop")	break;
		strs.push_back(input);
	}
	cout << "Please enter the maximum '0' numbers and '1' numbers:" << endl;
	int m, n;
	cin >> m >> n;
	cout << "The maximum subset's elements is: " << ms.findMaxFormvector(strs, m, n) << endl;
	return 0;
}