目录
引言
一、泰勒公式
1.泰勒公式及推导
(1)推导
(2)公式
2.泰勒中值定理
(1)定理1(佩亚诺余项)
(2)定理2(拉格朗日余项)
(3)两个定理的区别
3.麦克劳林公式
二、常用的泰勒公式
三、泰勒公式核心考点
1.求极限
2.求高阶导
3.证明题
总结
ID:HL_5461
引言
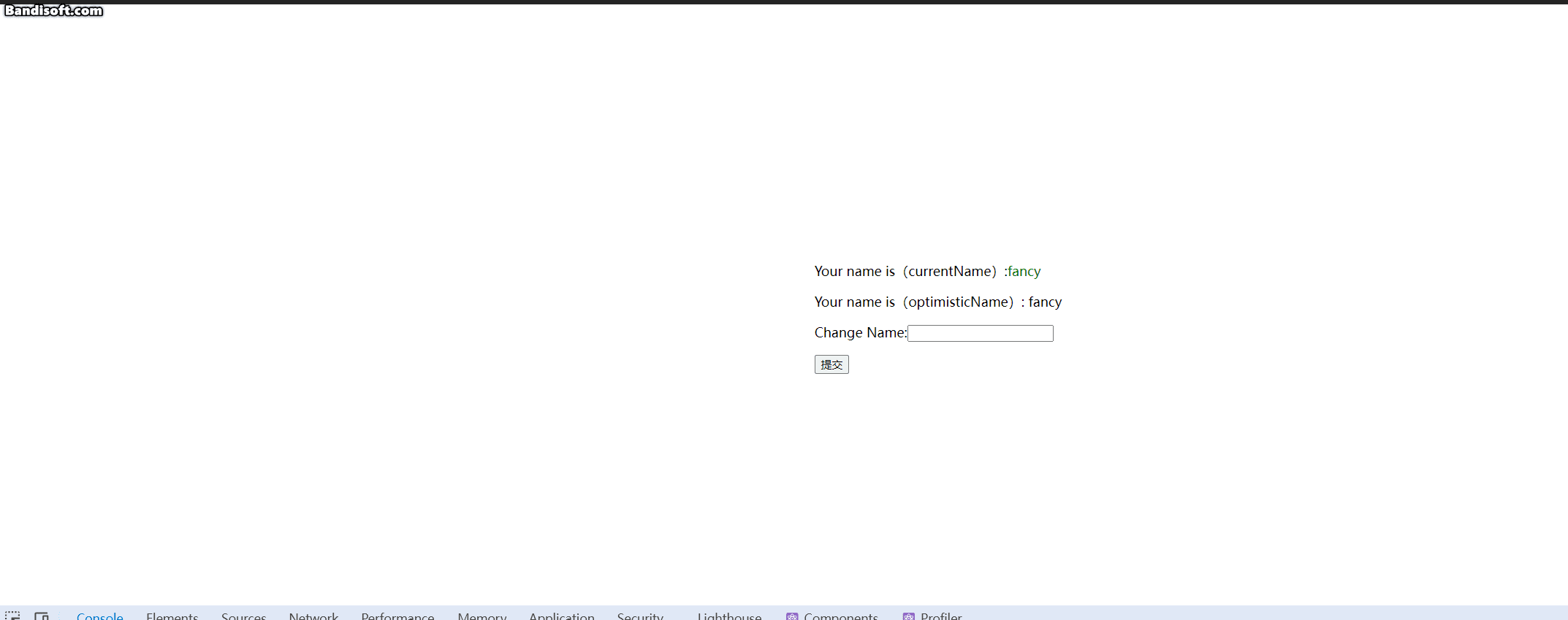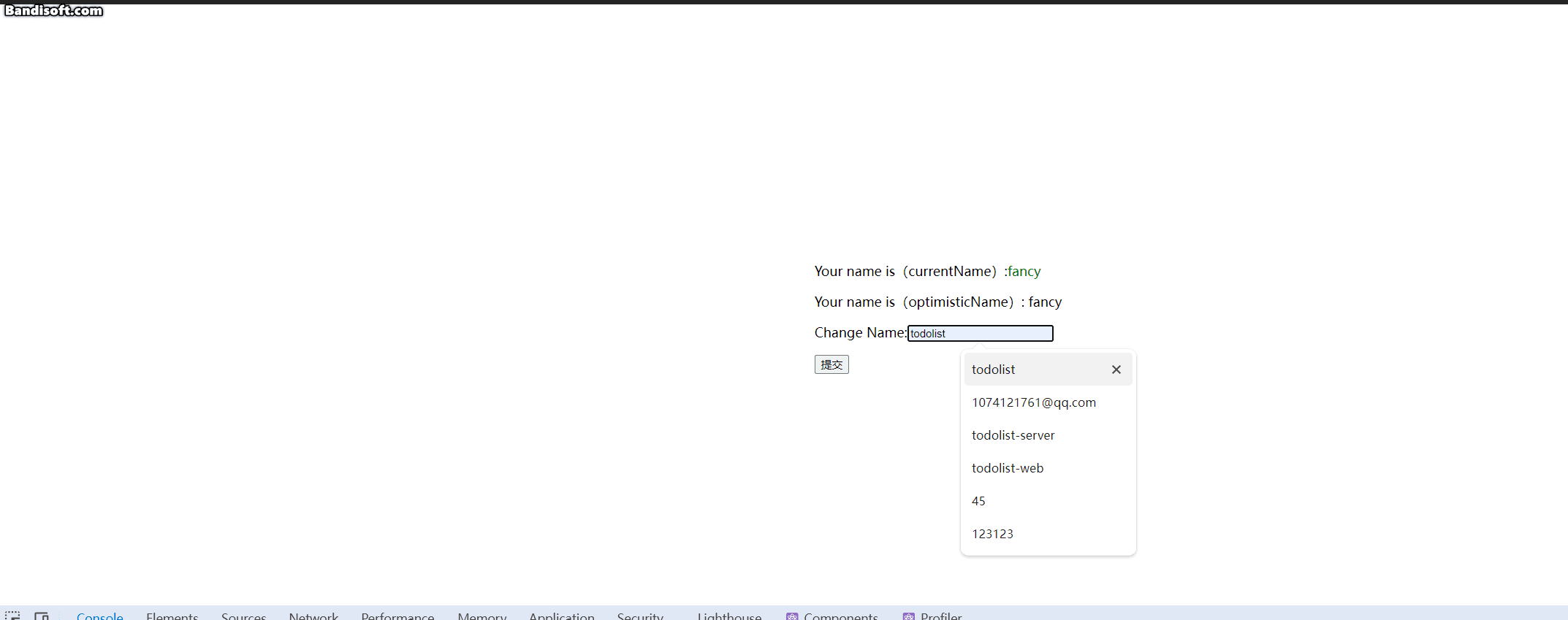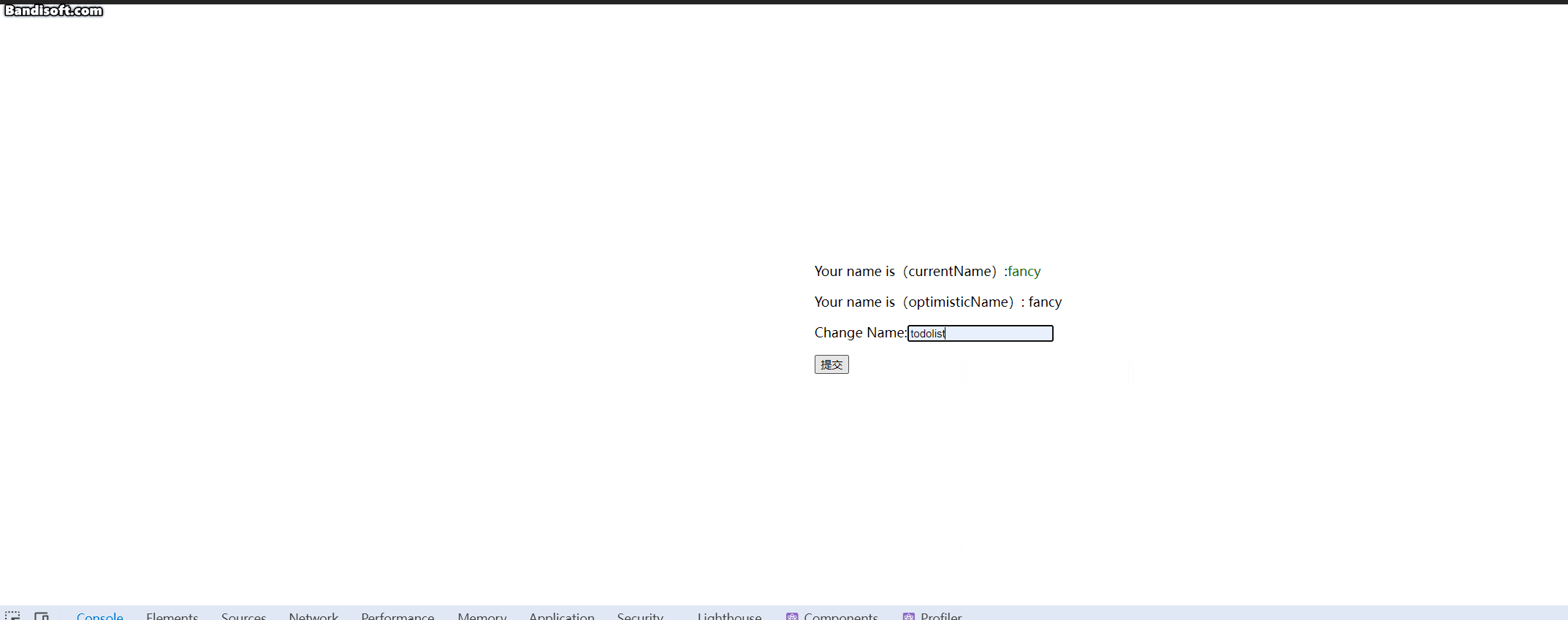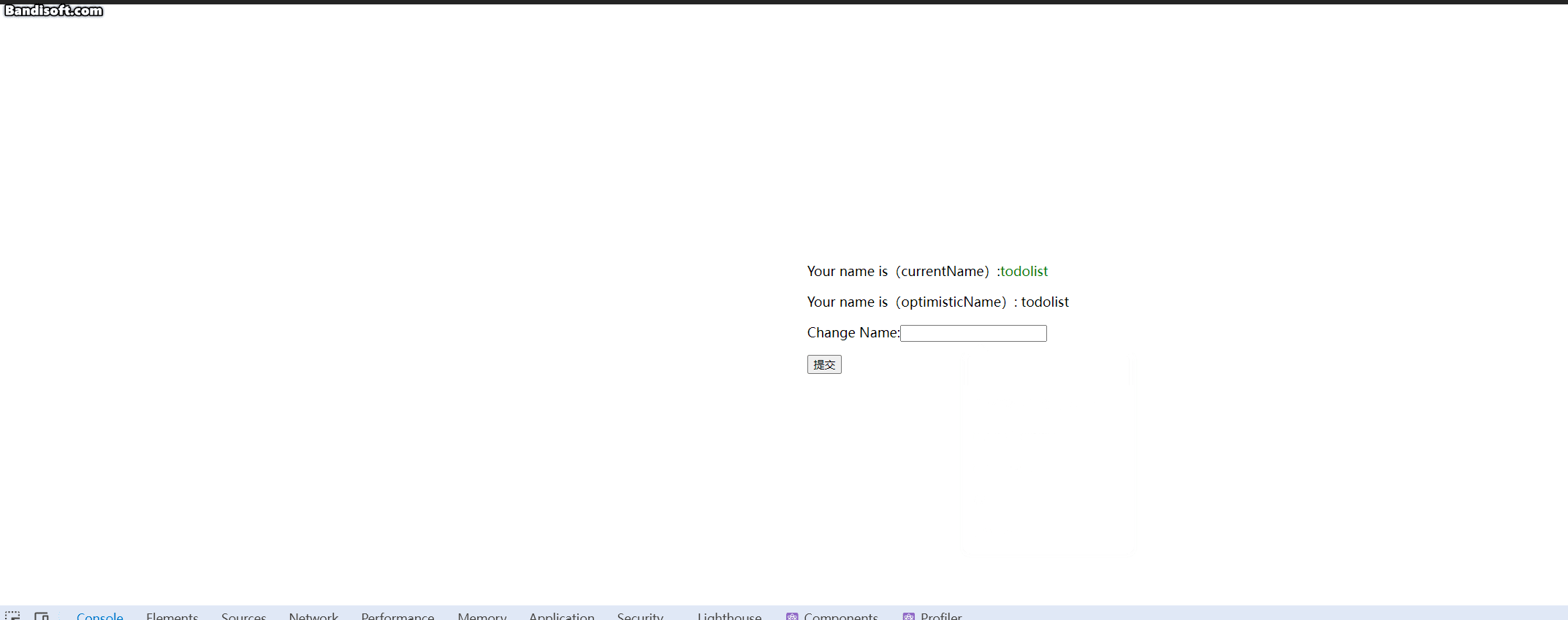
对于任意无穷数,这里以为例,我们可以用多个
的次方将其不断展开,即
类比的,对于一个函数,我们也可以将它写作无穷多x的次方展开,即
这也就是泰勒公式的诞生。
当然就像有限个的次方不能精确表示一个无穷小数一样,上述式子肯定有一定的误差,这个后文讨论。
一、泰勒公式
1.泰勒公式及推导
(1)推导
我们将引言中所写式子记作,所以有:
正如前面所说,这个式子有一定的误差,不能准确表示,所以我们退而求其次,选择让这个式子无限接近
,即
是
的高阶无穷小。
接下来的任务是确定系数。我们先定一个条件:设
在
处n阶可导。
那么如何让非常接近
呢?只需满足两个条件:1.
与
在
处函数值相等;2.
与
在
处直到n阶倒数相等。
我们可以这样理解上面两个条件:函数值相等说明在同一个点处,导数相等说明函数变化一样,值一样变化一样,所以可以近似看作相等。以下是的推导过程:
1
与
在
处函数值相等
,
2
对
与
求一阶导,并带入
,
3
对
与
求二阶导,并带入
,
4
不断求导、总结,所以:
(2)公式
将前面算出的带入
,所以:
由于在引言中说过,如果与
相比有一定误差,所以这里补充一个误差项就能与
相等了。我们将这个误差项称为余项,记作
。
所以泰勒公式就是如下形式:
除了
的前半部分是
在
处的n次多项展开式
称为余项,也是一个误差项
2.泰勒中值定理
泰勒中值定理是对余项的讨论。
(1)定理1(佩亚诺余项)
设
在
处具有直到n阶的导数,则有
其中,
,
称为佩亚诺(Peano)余项。
该展开式称为
在点
邻域的带佩亚诺余项的n阶泰勒公式。
(2)定理2(拉格朗日余项)
设
在包含
的区间
内有直到n+1阶的导数,在区间
上有n阶连续导数,则对任意
时有
其中,
,(
在
与
之间)称为拉格朗日余项。
该展开式称为
在区间
的带拉格朗日余项的n阶泰勒公式。
注:对于拉格朗日余项的泰勒公式,根据定义,题目如果说在区间上有n+1阶的导数,那么做题时需展到n阶,n+1阶留给余项。
(3)两个定理的区别
这里可以结合前面定理内容加粗部分理解
1.成立条件不同。定理2对
的可导性要求更高。2要求区间可导,1只要求点可导;2要求可导至n+1阶,1只要求可导至n阶。
2.x的取值范围不同。定理1需满足
,仅适用于求极限问题;定理2中
可在符合条件的区间
上任取,甚至能取到任意实数,因此中值定理2更广泛地适用于证明题和近成似计算问题。
3.余项形式不同,佩亚诺余项便于求极限,而拉格朗日余项能具体估算近似误差的大小。
3.麦克劳林公式
麦克劳林公式就是令时的泰勒公式:
二、常用的泰勒公式
三、泰勒公式核心考点
1.求极限
方法:按上面给的重要泰勒公式无脑代入
例1:
求极限
将上面式子带入极限:
例2:
设求a,b
代入极限
例3:
设二阶可导,
,求极限
由泰勒公式形式可得:
代入极限:
2.求n阶导数值
方法:依旧上述重要泰勒公式无脑往里代
例1:
求函数在
处的n阶导数
由泰勒公式的唯一性,第n项为
3.证明题
方法:
1.使用拉格朗日余项,对n+1阶可导,展到第n阶
2.和
依题目选择
(证明题比较难,下面讲解会解释思路)
例1:
设在
上二阶可导,且
,求证:
思路:
首先写出公式,因为二阶可导所以展到一阶:
,(
在
与
之间)
由于题目中告知
和
,所以不妨猜测
,代入公式:
在定义域内。
又
代入证毕
这题因为告知导数所以优先猜测
的值,将
代入和相关条件用完之后会发现已经做出来了,所以
的值就无需考虑了
例2:
在
上二阶可导,
,证明
,使得
思路:
首先写出公式,因为二阶可导所以展到一阶:
,(
在
与
之间)
由于题目中未提及导数相关,所以不妨猜测0和1是
,代入公式:
..............1
......2
0和1的相关条件似乎已经用完了
仔细查看上两式,会感觉
的缺少真的很碍眼,难道0和1应该用作
吗?但是如果换作
会发现这样只会减少
一个未知量,并且这样做还会多
一个未知量,好像和上两式没什么区别,所以暂时假定这个思路还是对的,接着往下看(下面是难点)
仔细思考一下
,由于
的缺少所以尽量往
上去想:如何才能有一个
和一个
?结合在区间上的最大值,我们可以联想到极大值。
假定极大值为
,则
,令
取
,则1、2式分别为:
于题目中未提及导数相关,所以不妨猜测0和1是
,代入公式:
..............3
..........4
在
的取值范围内,
和
有确定值,分类讨论能得出
和
的范围
再看题目要求是“存在”,找到一个就OK,所以证毕
这题没有告知导数相关,所以优先猜测
的值,将
代入后发现条件不够,再往后考虑
相关,联系极值,假设并代入,最后可以求得范围
例3:
设在
上二阶可导,且
,其中a,b都是非负常数,证明
思路:
首先写出公式,因为二阶可导所以展到一阶:
,(
在
与
之间)
由于题目中提及
和
,猜测告知条件为
,又加上
在
的取值范围内这一常用隐含条件,则:
到这一步已经条件用完,但是已经无路可走了,所以推翻重来
但是如果改用
,除了泰勒公式原式整个小于等于
啥也做不了,所以再换个思路,试着找点代代
题目没告知什么特殊值,那就只有拿0和1这两个端点试一试了
还是顾及题目给了导数,优先考虑
......................................1
................2
两式相减再取绝对值进行放缩,发现和前面没什么区别,那就改取
.................3
.........4
4-3得:
跟题目要求的
好像有点相像,既然有可能那就先往下做了再说
考虑一下如何把这个碍眼的
替换成题目需要的
(重点)
往定义上想,
是指代确定的
值,但是对于泰勒公式本身,
是可以在定义域上任取的,也就说对定义域上的任意
其实都有上式成立
也就说当
,都有
,这样一来
就成了题目需要的
了
(这里只是为了便于讲解所以放到了后面讨论,写题时可以在写3、4式时直接把
写成
)
对上式取绝对值
然后进行放缩:
把题目给的小于等于条件代入继续放缩:
由于
,继续代入放缩,证毕
这题比较难,还是按照一贯的思路来:因为告知导数所以优先猜测使用
,没用换成
,还是做不出来,继续代值考虑
、
最后发现
可以一试。这题主要还是在于端点值也可以使用这一容易忽视的细节和如何将
考虑作整个定义域上的
值两个难点。
总结
对于泰勒公式题目,首先还是几个重要公式熟背,这样就可以解决大部分题目了。
证明题是泰勒公式的难点,一般使用定理二结合放缩就能解决了,关键在于如何选择和
,这是解决证明题的核心。
若有错误,欢迎大家批评斧正!




![NSSCTF | [SWPUCTF 2021 新生赛]jicao](https://img-blog.csdnimg.cn/direct/c94a49ce360a4ba9ba2bc00132a3cad5.png)