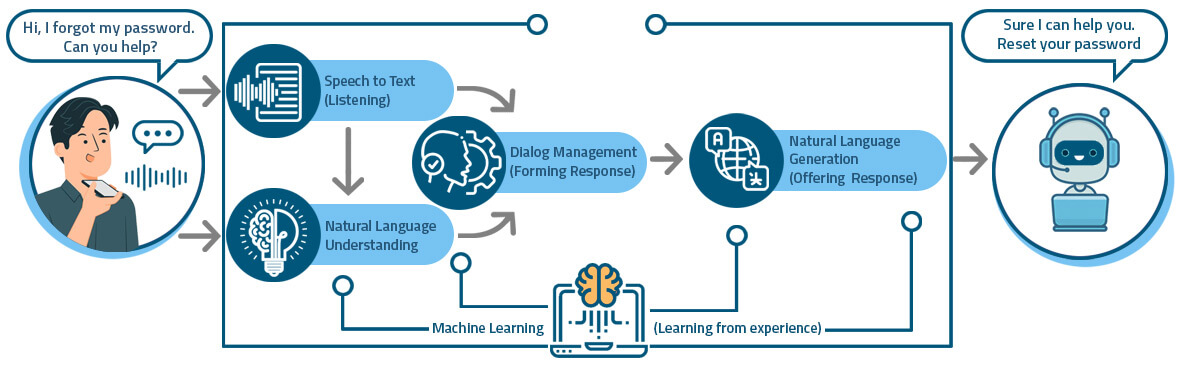
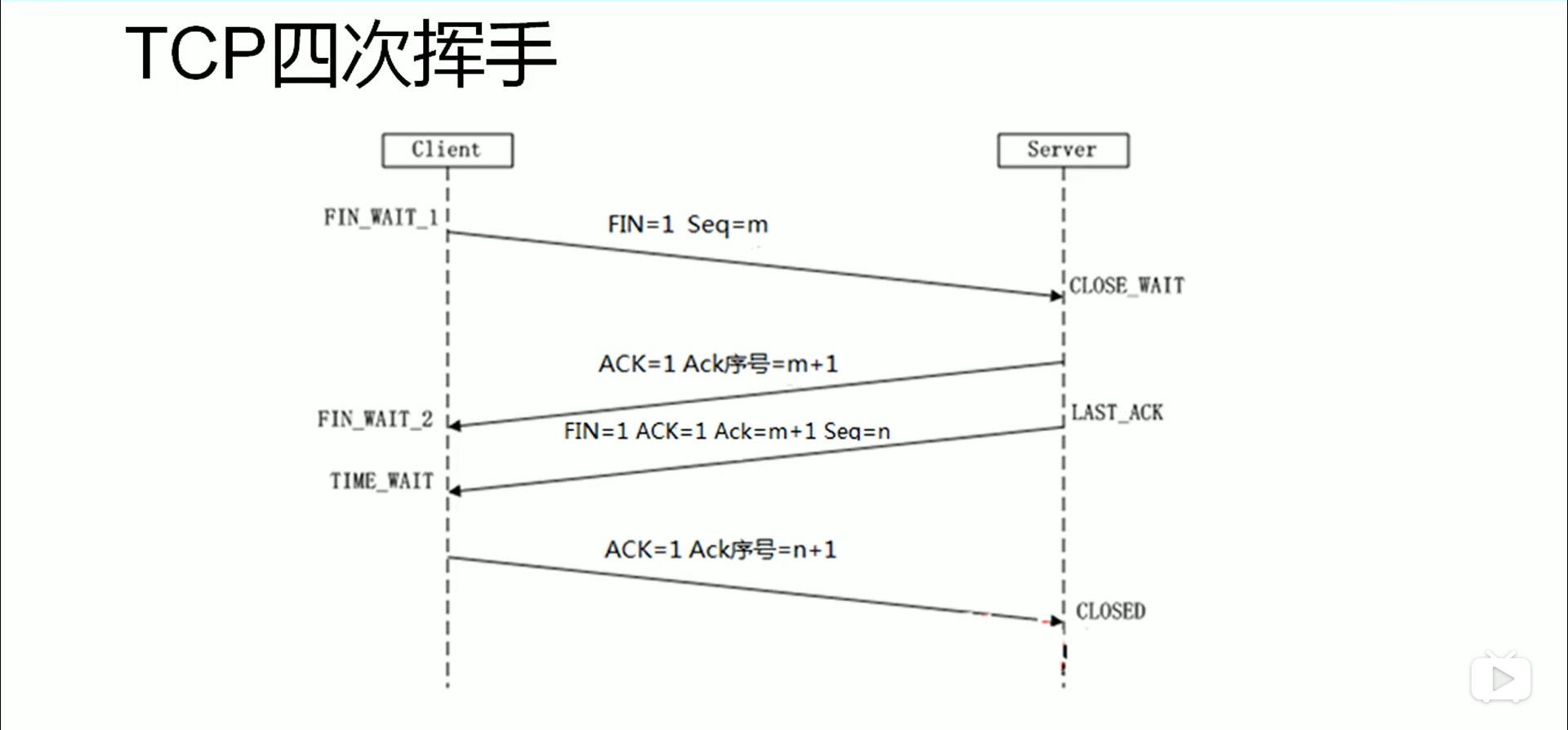
动机
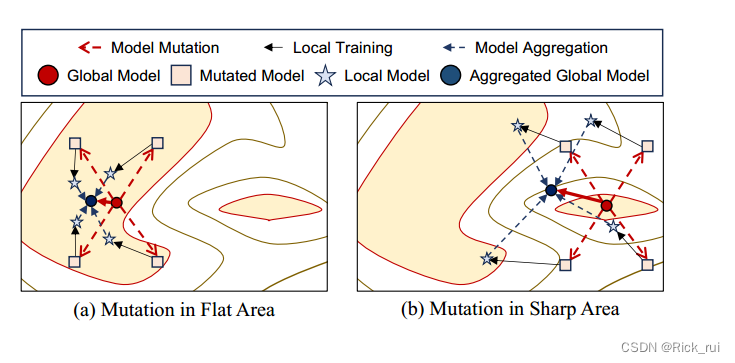
Many previous works observed that the well-generalized solutions are located in flat areas rather than sharp areas of the loss landscapes.
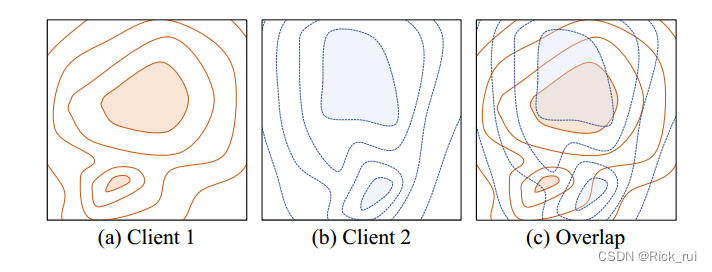
通常,由于每个本地模型的任务是相同的,因此每个客户端的损失情况仍然相似。直观上,与尖锐的最佳区域相比,不同客户端的平坦最佳区域部分重叠的可能性更大。换句话说,当模型收敛到重叠区域时,它可以在大多数客户端中实现高推理性能。
怎么做能达到效果?
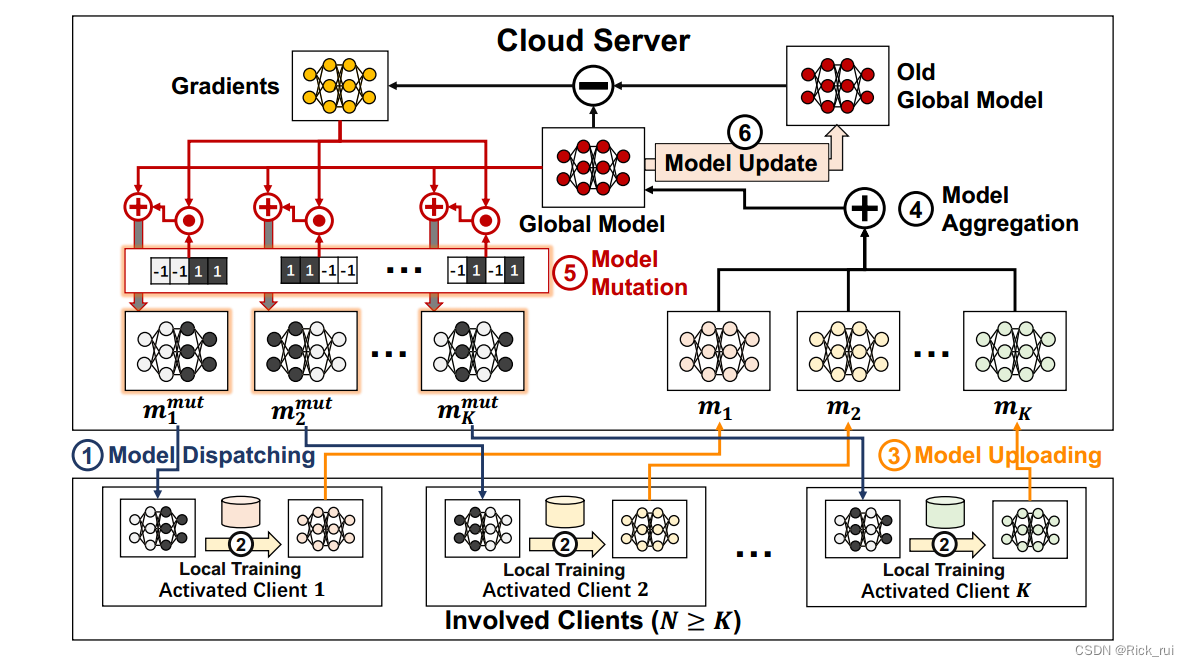
FedMut框架
global model :
ω
g
l
b
=
{
l
a
y
e
r
1
,
l
a
y
e
r
2
,
.
.
.
,
l
a
y
e
r
L
}
.
\omega_{glb} = \{ layer_1, layer_2,..., layer_L \}.
ωglb={layer1,layer2,...,layerL}.
gradients of
ω
g
l
b
\omega_{glb}
ωglb :
g
g
l
b
=
{
l
g
1
,
l
g
2
,
.
.
.
,
l
g
L
}
.
g_{glb} = \{lg_1, lg_2,..., lg_L\}.
gglb={lg1,lg2,...,lgL}.
mutation weight list
L
m
u
t
i
L^{i}_{mut}
Lmuti:
L
m
u
t
i
=
{
v
1
i
,
v
2
i
,
.
.
.
,
v
L
i
}
.
L^{i}_{mut}=\{v^i_1, v^i_2,..., v^i_L\}.
Lmuti={v1i,v2i,...,vLi}.
mutated model
ω
m
u
t
i
\omega^{i}_{mut}
ωmuti
ω
m
u
t
i
=
{
l
a
y
e
r
1
+
α
v
1
i
⋅
l
g
1
,
.
.
.
,
l
a
y
e
r
L
+
α
v
L
i
⋅
l
g
L
}
\omega^{i}_{mut} = \{layer_1+\alpha v^i_1 \cdot lg_1 ,..., layer_L+\alpha v^i_L \cdot lg_L\}
ωmuti={layer1+αv1i⋅lg1,...,layerL+αvLi⋅lgL}
算法