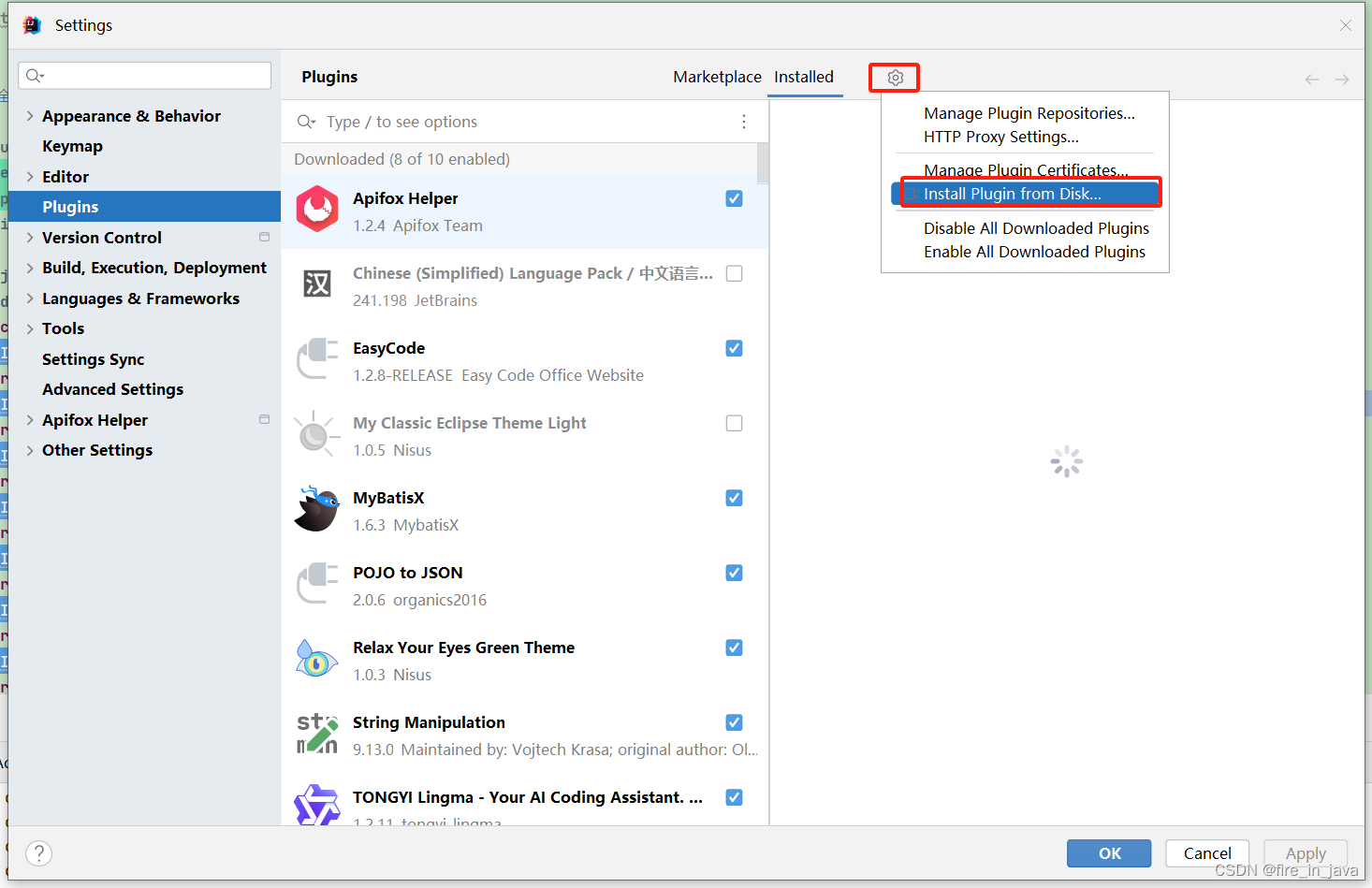
机器人学

1. 刚体运动

1.1 刚体变换

三维空间中可以用坐标$(x,y,z)\in {\mathcal{R}}^3$来描述质点的位置，而质点的运动轨迹可以使用参数形式来进行表示：$p(t)=(x(t),y(t),z(t))\in {\mathcal{R}}^3$。在机器人学中，我们通常关心的问题通常不是一个质点的运动，而是一组质点共同的运动。如果一条杆上的质点保持相对距离不变，我们认为其是一个不变的形体，可以严格定义刚体如下：

刚体

刚体（rigid body）是任意两质点之间距离保持不变的质点的集合，并与物体的任意运动和作用在物体上的任意力无关。用数学的表示即是：
$$||p(t)-q(t)||=||p(0)-q(0)||$$

刚体变换

刚体变换（rigid body transformation），满足以下条件的变换$g:{\mathcal{R}}^3\to {\mathcal{R}}^3$，被称为刚体变换：

1. 长度不变，对于任意的点$p,q\in {\mathcal{R}}^3$，均有$||g(p)-g(q)||=||p-q||$；
2. 叉积不变，对于任意的矢量$v,w\in {\mathcal{R}}^3$，均有$g_{\ast }(v\times w)=g_{\ast }(v)\times g_{\ast }(w)$。

刚体上任意两点之间的距离以及任意两矢量之间的叉积固定不变并不意味着刚体上质点建不能有相对运动，只是这些运动只能是旋转而不能是移动。

1.2 三维空间中的旋转运动

设A为惯性坐标系，B为与刚体固连的动坐标系，$x_{ab},y_{ab},z_{ab}\in {\mathcal{R}}^3$为坐标系B中主坐标轴相对于A坐标系的坐标，依次排列这三个坐标矢量，就构成了一个3x3的矩阵：
$$R_{ab}=[x_{ab},y_{ab},z_{ab}]\in {\mathcal{R}}^{3\times 3}$$

按照这种方式构建的矩阵被称为旋转矩阵（rotation matrix）：物体相对于定坐标系的每一次旋转都对应一个该形式的旋转矩阵。旋转矩阵也可称为位姿（configuration）

旋转矩阵满足以下的性质，设$R\in {\mathcal{R}}^{3\times 3}$为旋转矩阵，$r_1,r_2,r_3\in {\mathcal{R}}^3$为其列矢量，因为旋转矩阵$R$的列矢量是相互正交的所以则有：
$$r_i^T{r}_j=\{\begin{array}{r}0,\text{if }i\ne j\\ 1,\text{if }i=j\end{array}$$
写成矩阵的形式则有，$R{R}^T=R^{T}R=I$，$detR=\pm 1$

群

群（group）定义如下，对于元素可用算子$\circ$构成二元运算的集合$G$，若满足以下条件则被成为群：

1. 封闭性：若$g_1,g_2\in {\mathcal{R}}^{3\times 3}$，则$g_1\circ g_2\in G$；
2. 单位性：对于任意的$g\in G$，一定存在一个单位元素$e$，使得$g\circ e=e\circ g=g$；
3. 可逆性：对于任意的$g\in G$，一定存在唯一的逆$g^{-1}\in G$，使得$g\circ g^{-1}=g^{-1}\circ g=e$；
4. 结合性：若$g_1,g_2,g_3\in G$，则有$(g_1\circ g_2)\circ g_3=g_1\circ (g_2\circ g_3)$

所有旋转矩阵的集合满足群的性质，被称为$SO(3)$，符号$SO(3)$是special orthogonal的缩写，$SO(3)$是一个群。

求质点坐标的相对变换

如果坐标系A和坐标系B之间只存在旋转变换，$q$在B坐标系中的坐标为$q_b=(x_b,y_b,z_b)$，且已知坐标系B相对于坐标系A的旋转矩阵为$R_{ab}=[x_{ab},y_{ab},z_{ab}]\in {\mathcal{R}}^{3\times 3}$，那么$q$在A坐标系中的坐标为
$$q_a=\left[\begin{array}{ccc}{x}_{ab}& y_{ab}& z_{ab}\end{array}\right]\left[\begin{array}{c}{x}_b\\ y_b\\ z_b\end{array}\right]=R_{ab}{q}_b$$
即旋转矩阵$R_{ab}$表示一点从坐标系B到坐标系A坐标的旋转变换（不包含平移变换）。

旋转矩阵的合成法则

旋转矩阵可以通过矩阵相乘加以结合，从而形成新的旋转矩阵。如果坐标系C相对于坐标系B的姿态为$R_{bc}$，坐标系B相对于另一坐标系A的姿态为$R_{ab}$，那么，坐标系C相对于坐标系A的位形为
$$R_{ac}=R_{ab}{R}_{bc}$$

用线性算子来计算叉积

有两个矢量$a=[a_1,a_2,a_3{]}^T,b=[b_1,b_2,b_3{]}^T$，两矢量的叉积结果为：
$$a\times b=\left[\begin{array}{c}{a}_2{b}_3-a_3{b}_2\\ a_3{b}_1-a_1{b}_3\\ a_1{b}_2-a_2{b}_1\end{array}\right]$$
可以表示为$a\times b=\hat{a}b$，其中
$$\hat{a}=\left[\begin{array}{ccc}0& -a_3& a_2\\ a_3& 0& -a_1\\ -a_2& a_1& 0\end{array}\right]$$
这样可以简便地计算叉积。

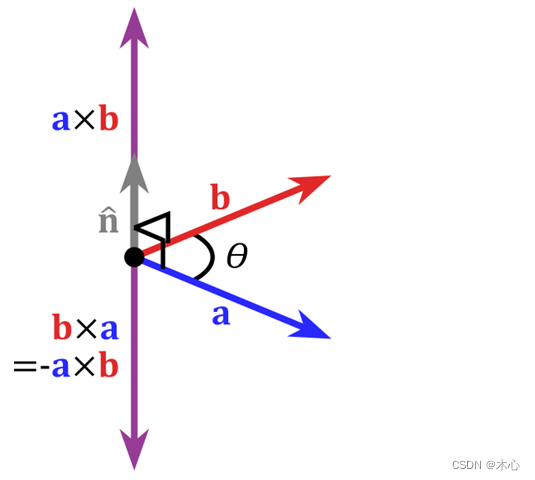
叉积的右手法则

叉积的概念非常有用，可以通过两个向量的叉乘，生成第三个垂直于a，b的法向量，从而构建X、Y、Z坐标系。如下图所示，用右手从叉积符号前的矢量转向叉积符号后的矢量，大拇指的指向就为结果矢量的方向。叉积在三维空间中的意义是生成一个垂直于两个矢量的新矢量，叉积在二维空间中的意义是两矢量所构成的平行四边形的面积。

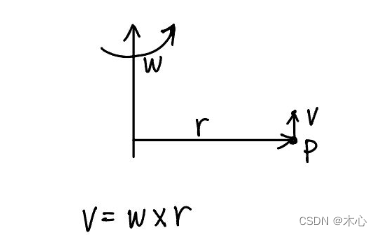
叉积用于计算线速度

线速度$v$是角速度$\omega$（角速度的方向为旋转轴的方向）与垂直于旋转轴且指向质点的矢量$r$的叉积，
$$v=\omega \times r$$
如图所示：

旋转的指数坐标

设$\omega \in {\mathcal{R}}^3$是表示旋转方向的单位矢量，$\theta \in \mathcal{R}$为旋转角度，物体的每次转动都存在一个旋转矩阵$R\in SO(3)$与之对应，因此可以将旋转矩阵$R$表示为旋转轴$\omega$和旋转角度$\theta$的函数。推导过程如下：

已知刚体上一质点的速度$v$与角速度$w$满足关系$v=w\times r$，$r$为旋转轴到质点的矢量。考虑旋转体上一质点$q$的速度，物体以单位角速度绕$\omega$作匀速旋转，那么$q$点的速度$\dot{q}$可以表示为：
$$\dot{q}(t)=\omega \times q(t)=\hat{\omega }q(t)$$
求解这个微分方程可以得到
$$q(t)=e^{\hat{\omega }t}q(0)$$
其中$q(0)$是质点$q$的起始位置，$e^{\hat{\omega }t}$是矩阵指数，由矩阵分析的知识可以知道，该矩阵指数可以进行展开如下：
$$e^{\hat{\omega }t}=I+\hat{\omega }t+\frac{(\hat{\omega }t{)}^2}{2!}+\frac{(\hat{\omega }t{)}^3}{3!}+\cdots$$
又由于已经规定了旋转的角速度为单位角速度，那么旋转矩阵就可以写成旋转轴$\omega$和旋转角度$\theta$的函数了:
$$R(\omega ,\theta )=e^{\hat{\omega }\theta }$$
算子$\hat{\omega }$是反对称阵，满足${\hat{\omega }}^T=-\hat{\omega }$，我们将所有这种$3\times 3$的反对称阵组成的矢量空间记为$so(3)\in SO(3)$。

Rodrigues公式

对于前面提到的矩阵指数$e^{\hat{\omega }\theta }$，我们难以直接计算，我们需要借助Taylor展开来进行化简。首先，我们需要指导算子$\hat{\omega }$的幂是怎么计算的：
$$\begin{gathered} {\hat{\omega }}^2=\omega {\omega }^T-||\omega |{|}^{2}I \\ {\hat{\omega }}^3=-||\omega |{|}^2\hat{\omega } \end{gathered}$$
且规定了以单位速度进行旋转，则$||\omega ||=1$，那么之前的Taylor展开可以化简为：
$$e^{\hat{\omega }\theta }=I+(\theta -\frac{{\theta }^3}{3!}+\frac{{\theta }^5}{5!}-\cdots )\hat{\omega }+(\frac{{\theta }^2}{2!}-\frac{{\theta }^4}{4!}+\frac{{\theta }^6}{6!}-\cdots ){\hat{\omega }}^2$$
然后再根据$\sin \theta$和$\cos \theta$的Taylor展开可以进一步化简为：
$$e^{\hat{\omega }\theta }=I+\hat{\omega }\sin \theta +{\hat{\omega }}^2(1-\cos \theta )$$
当$||w||\ne 1$的时候，上述公式可以修正为：
$$e^{\hat{\omega }\theta }=I+\frac{\hat{\omega }}{||\omega ||}\sin (||\omega ||\theta )+\frac{{\hat{\omega }}^2}{||\omega |{|}^2}(1-\cos (||\omega ||\theta ))$$
这就是用于计算旋转矩阵$R$的Rodrigues公式。

计算旋转矩阵的例子

让我们举一个例子，假设我们要绕单位向量$u=[0,0,1{]}^T$（绕z轴）旋转$\theta =\frac{\pi }{2}$弧度，我们使用Rodrigues’ formula来计算旋转矩阵：

首先计算反对称矩阵$\hat{u}$
$$\begin{gathered} \hat{u}=\left[\begin{array}{ccc}0& -u_z& u_y\\ u_z& 0& -u_x\\ -u_y& u_x& 0\end{array}\right]=\left[\begin{array}{ccc}0& -1& 0\\ 1& 0& 0\\ 0& 0& 0\end{array}\right] \\ {\hat{u}}^2=\left[\begin{array}{ccc}-1& 0& 0\\ 0& -1& 0\\ 0& 0& 0\end{array}\right] \end{gathered}$$
然后带入Rodrigues公式
$$\begin{array}{rl}{R}_z(\theta )& =I+\sin \theta \hat{u}+(1-\cos \theta ){\hat{u}}^2\\ & =\left[\begin{array}{ccc}1& & \\ & 1& \\ & & 1\end{array}\right]+\left[\begin{array}{ccc}0& -\sin \theta & 0\\ -\sin \theta & 0& 0\\ 0& 0& 0\end{array}\right]+\left[\begin{array}{ccc}\cos \theta -1& 0& 0\\ 0& \cos \theta -1& 0\\ 0& 0& 0\end{array}\right]\\ & ={\left[\begin{array}{ccc}\cos \theta & -\sin \theta & 0\\ \sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right]}_{\theta =\frac{\pi }{2}}\\ & =\left[\begin{array}{ccc}0& -1& 0\\ 1& 0& 0\\ 0& 0& 1\end{array}\right]\end{array}$$

四元数

四元数（quafernions）是复数的推广，四元数通过四个数来描述旋转运动，给出了$SO(3)$的一个全局参数表示法。四元数是一个矢量，其一般的表示形式为：
$$Q=q_0+q_{1}i+q_{2}j+q_{3}k$$
其中$q_0$为$Q$的标量部分，$q=(q_1,q_2,q_3)$为矢量部分。

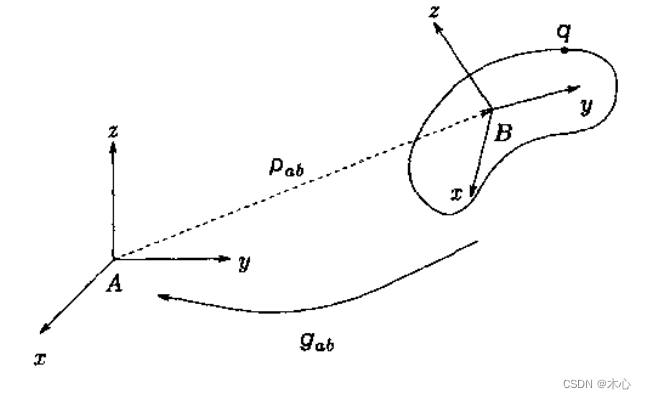
1.3 三维空间中的刚体运动

通常来说，刚体运动包括旋转和平移两部分。如图描述固定于刚体上的动坐标系B相对于惯性坐标系A的位姿，设坐标系A的原点至坐标系B的原点的位置矢量为$p_{ab}\in {\mathcal{R}}^3$，B系相对于A系的姿态为$R_{ab}\in SO(3)$。B系相对于A系的运动包括平移$p_{ab}$和旋转$R_{ab}$，所以系统的位姿由$g_{ab}=(p_{ab},R_{ab})$确定，系统的位形空间为${\mathcal{R}}^3$与$SO(3)$的乘积空间，记为$SE(3)$，意为：Special Euclidean
$$SE(3)=|(p,R):p\in {\mathcal{R}}^3,R\in SO(3)|={\mathcal{R}}^3\times SO(3)$$

与旋转的情况类似，元素$g=(p,R)\in SE(3)$既可以用于确定刚体的位形，又可以用于由一点的坐标到另一坐标系的坐标变换。若，$q_a,q_b\in {\mathcal{R}}^3$是分别属于A系和B系的坐标，当已知$q_b$时，$q_a$可以通过坐标变换来得到
$$\begin{array}{rl}{q}_a& =g_{ab}(q_b)\\ q_a& =p_{ab}+R_{ab}{q}_b\end{array}$$
其中$g_{ab}=(p_{ab},R_{ab})\in SE(3)$表示B系相对于A系的位形，用符号$g(q)$来表示这一刚体变换，即：
$$g(q)=p+Rq$$

齐次坐标表示法

为了使包含平移和旋转的刚体变换更简单（像纯旋转变化那样通过一个矩阵运算就能表示），所以引入了齐次坐标表示法。

首先给质点的坐标增加一个维度，最后一个维度设置为1，组成一个四维矢量（称为齐次坐标）：
$$\bar{q}=[q_1,q_2,q_3,1{]}^T$$
矢量是通过质点的坐标相减获得的，所以矢量的齐次表示为：
$$\bar{v}=[v_1,v_2,v_3,0{]}^T$$
矢量和点的齐次坐标表示的第四个分量分别为0和1，请注意这一个差别。将上述的刚体变换$q_a=p_{ab}+R_{ab}{q}_b$写成矩阵的形式：
$${\bar{q}}_a=\left[\begin{array}{c}{q}_a\\ 1\end{array}\right]=\left[\begin{array}{cc}{R}_{ab}& p_{ab}\\ 0& 1\end{array}\right]\left[\begin{array}{c}{q}_b\\ 1\end{array}\right]=:{\bar{g}}_{ab}{\bar{q}}_b$$
${\bar{g}}_{ab}$称为$g_{ab}\in SE(3)$的齐次表示。通常，若$g=(p,R)\in SE(3)$，那么
$$\bar{g}=\left[\begin{array}{cc}R& p\\ 0& 1\end{array}\right]$$

齐次表示刚体变换的逆

如果$g=(p,R)\in SE(3)$，那么$\bar{g}$的逆可以由矩阵的逆来进行确定
$${\bar{g}}^{-1}=\left[\begin{array}{cc}{R}^T& -R^{T}p\\ 0& 1\end{array}\right]$$

刚体变换的组合

刚体变换的组合将构成新的刚体变换，若$g_{bc}\in SE(3)$表示坐标系C相对于坐标系B的位形，$g_{ab}$表示B系相对于A系的为形，那么通过齐次表示可以获得C系相对于A系的位形
$$\begin{array}{rl}{\bar{g}}_{ac}& ={\bar{g}}_{ab}{\bar{g}}_{bc}\\ & =\left[\begin{array}{cc}{R}_{ab}& p_{ab}\\ 0& 1\end{array}\right]\left[\begin{array}{cc}{R}_{bc}& p_{bc}\\ 0& 1\end{array}\right]\\ & =\left[\begin{array}{cc}{R}_{ab}{R}_{bc}& R_{ab}{p}_{bc}+p_{ab}\\ 0& 1\end{array}\right]\end{array}$$

计算刚体运动的例子

考虑刚体绕平行于z轴且经过点$(0,l_1,0)\in {\mathcal{R}}^3$的一条直线的旋转运动，如图所示，求刚体位形的齐次表示

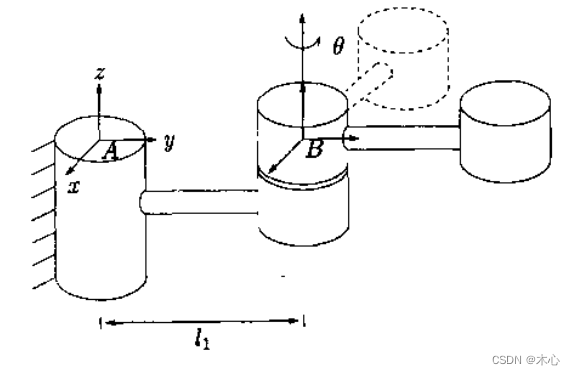
由之前的例子可以知道，B系相对于A系的姿态矩阵为：
$$R_{ab}=\left[\begin{array}{ccc}\cos \theta & -\sin \theta & 0\\ \sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right]$$
B系原点在A系中的坐标为
$$p_{ab}=\left[\begin{array}{c}0\\ l_1\\ 0\end{array}\right]$$
所以刚体位形的齐次表示矩阵为
$${\bar{g}}_{ab}(\theta )=\left[\begin{array}{cc}{R}_{ab}& p_{ab}\\ 0& 1\end{array}\right]=\left[\begin{array}{cccc}\cos \theta & -\sin \theta & 0& 0\\ \sin \theta & \cos \theta & 0& l_1\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$
在本文以下的表述中，刚体运动$g$的齐次表示不再使用$\bar{g}$来加以区分。

刚体运动的指数坐标和运动旋量

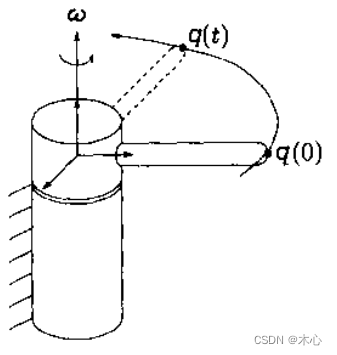
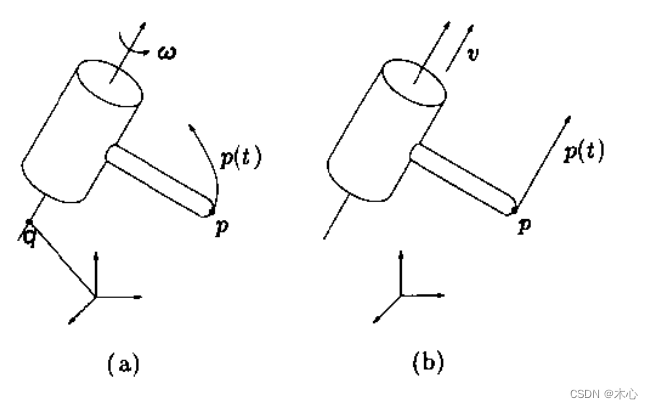
定义：运动旋量（twist）$\xi =[v,\omega {]}^T$，通常包含两个部分，分别是线速度$v$和角速度$\omega$。

考虑一个单臂机器人的旋转例子，如下图所示：

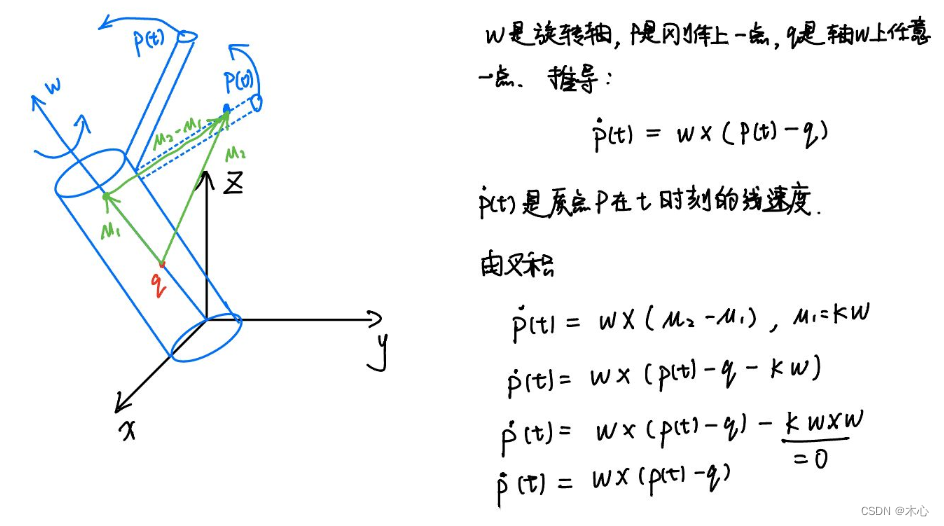
臂端点$p(t)$的线速度为：
$$\dot{p}(t)=\omega \times (p(t)-q)$$
将上述式子写成齐次的形式
$$\begin{array}{rl}\left[\begin{array}{c}\dot{p}\\ 0\end{array}\right]& =\left[\begin{array}{cc}\hat{w}& -\omega \times q\\ 0& 0\end{array}\right]\left[\begin{array}{c}p\\ 1\end{array}\right]\\ \left[\begin{array}{c}\dot{p}\\ 0\end{array}\right]& =\hat{\xi }\left[\begin{array}{c}p\\ 1\end{array}\right]\end{array}$$
其中

$$\hat{\xi }=\left[\begin{array}{cc}\hat{w}& -\omega \times q\\ 0& 0\end{array}\right],v=-\omega \times q$$
上述微分方程的解为：
$$\bar{p}(t)=e^{\hat{\xi }t}\bar{p}(0)$$
其中$e^{\hat{\xi }t}\in R^{4\times 4}$被称为矩阵$\hat{\xi }t$的矩阵指数，可以展开为：
$$e^{\hat{\xi }t}=I+\hat{\xi }t+\frac{(\hat{\xi }t{)}^2}{2!}+\frac{(\hat{\xi }t{)}^3}{3!}+\cdots$$
如果是单位旋转角速度，那么$t$可以完全由$\theta$进行代替。

从这个例子我们可以得到旋量的意义和计算方式：
$$\begin{gathered} \xi =\left[\begin{array}{c}v\\ \omega \end{array}\right]=\left[\begin{array}{c}-\omega \times q\\ \omega \end{array}\right] \\ \hat{\xi }=\left[\begin{array}{cc}\hat{\omega }& v\\ 0& 0\end{array}\right] \end{gathered}$$
包含了一个绕轴$\omega$的旋转，和沿着$\omega$轴线的平移运动，如下图所示

可以把这个运动想象成拧螺丝，如下图所示

矩阵指数$e^{\hat{\xi }\theta }$可以通过如下方式来进行计算
$$g=e^{\hat{\xi }\theta }=\left[\begin{array}{cc}{e}^{\hat{\omega }\theta }& (I-e^{\hat{\omega }\theta })(\omega \times v)+\omega {\omega }^{T}v\theta \\ 0& 1\end{array}\right]$$
其中$e^{\hat{\omega }\theta }=I+\hat{\omega }\sin \theta +{\hat{\omega }}^2(1-\cos \theta )$，这是$SE(3)$中的元素，它与前面的刚体变换不同，它描述的不是点在不同坐标系之间的变换，而是点由初始位置$p(0)\in {\mathcal{R}}^3$到$p(\theta )\in {\mathcal{R}}^3$经过了如下刚体运动的位置坐标之间的变换
$$p(\theta )=e^{\hat{\xi }\theta }p(0)$$
上式子中，$p(0)$和$p(\theta )$均在同一参考系中。运动旋量的指数可以理解为描述刚体由起始位置到最终位形的变换。

Reference

[1]机器人操作的数学导论-MLS中文版