【模板】二维前缀和_牛客题霸_牛客网 (nowcoder.com)

理解题意：

要求的是(x1,y1) - (x2,y2)这段区间的和。

解法：二维前缀和

1. 和一维前缀和一样，需要有一个同等规模的dp数组，用来保存一段连续区域的和。

在二维dp中，可以把数组分为四部分，如下图：

dp[xi][yi] 求的是由(1,1) - (xi,yi)区域的和，就是算A+B+C+D的和。而在此中，直接求B,C的值可不好求，因为在之前的dp数组中找不到（这就与一维数组的dp不同了），所以结合一下，先求A+B,A+C的和，再减去多加的A即可。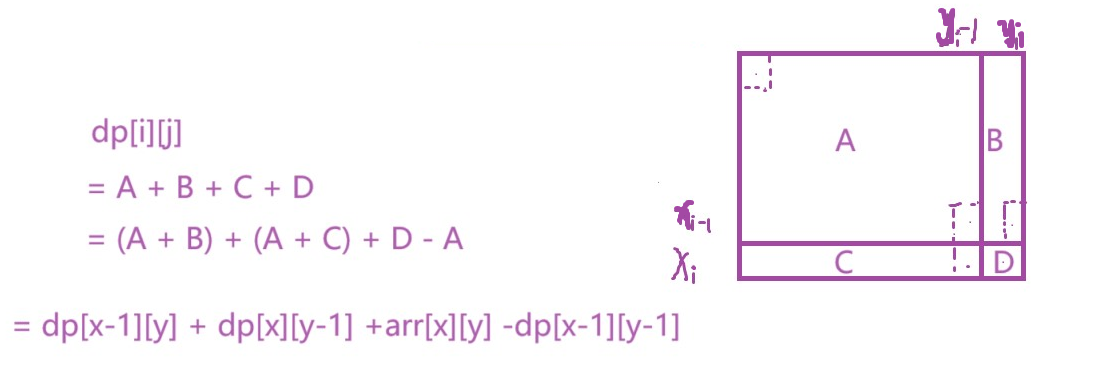

2.使用前缀和dp

要求的是中间一段区间的面积：D

int main() 
{
    //1.把值输入到原始数组
    int n = 0,m = 0,q = 0;
    cin >> n >> m >> q;
    vector<vector<int>> arr(n+1,vector<int>(m+1));
    for(int i = 1;i<=n;i++)
        for(int j = 1;j<=m;j++)
            cin >> arr[i][j];
    //2.创建dp数组
    vector<vector<long long int>> dp(n+1,vector<long long int>(m+1));
    for(int i = 1;i<=n;i++)
        for(int j = 1;j<=m;j++)
            dp[i][j] = dp[i-1][j] + dp[i][j-1] + arr[i][j] - dp[i-1][j-1];
    //3.使用dp数组
    int x1 = 0,y1 = 0,x2 = 0,y2 = 0;
    while(q--)
    {
        cin >> x1 >> y1 >> x2 >> y2;
        cout<< dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1] <<endl;
    }
}