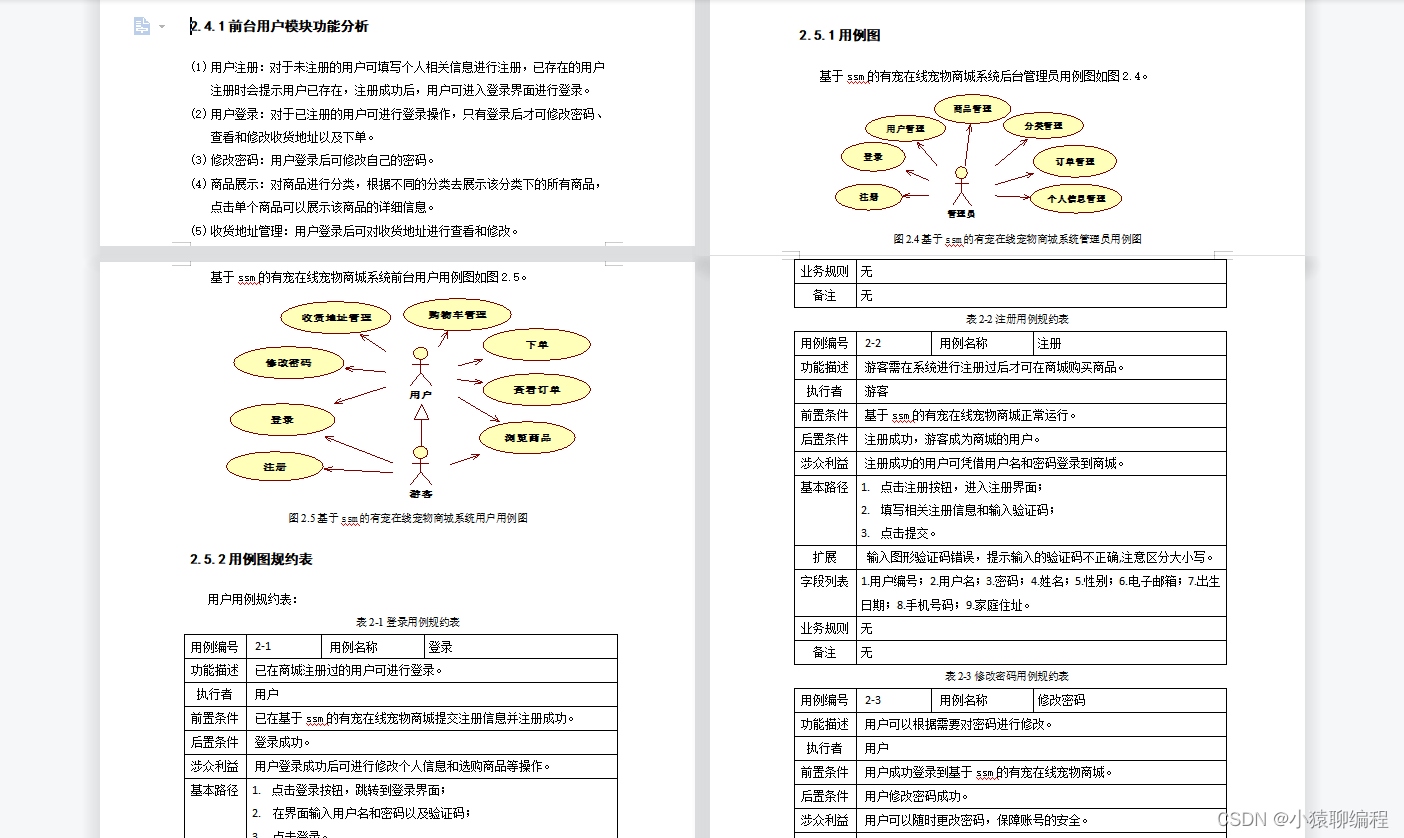
边缘概率密度图是一种在多变量数据分析中常用的图形工具，用于显示每个单独变量的概率密度估计。它通常用于散点图的边缘，以便更好地理解单个变量的分布情况，同时保留了散点图的相关性信息。

在边缘概率密度图中，每个变量的概率密度估计通常通过直方图或核密度估计（KDE）进行计算。直方图将变量的值范围分成若干个区间，并统计每个区间中观察值的数量，然后将数量除以总观察值数量得到概率密度。而核密度估计则是通过在每个数据点周围放置核函数，并根据核函数的形状和宽度来估计概率密度。

边缘概率密度图通常与散点图一起显示，其中散点图展示了两个变量之间的关系，而边缘概率密度图则展示了每个变量的分布情况。这有助于发现变量之间的相关性以及每个变量的个体特征。如下图所示：

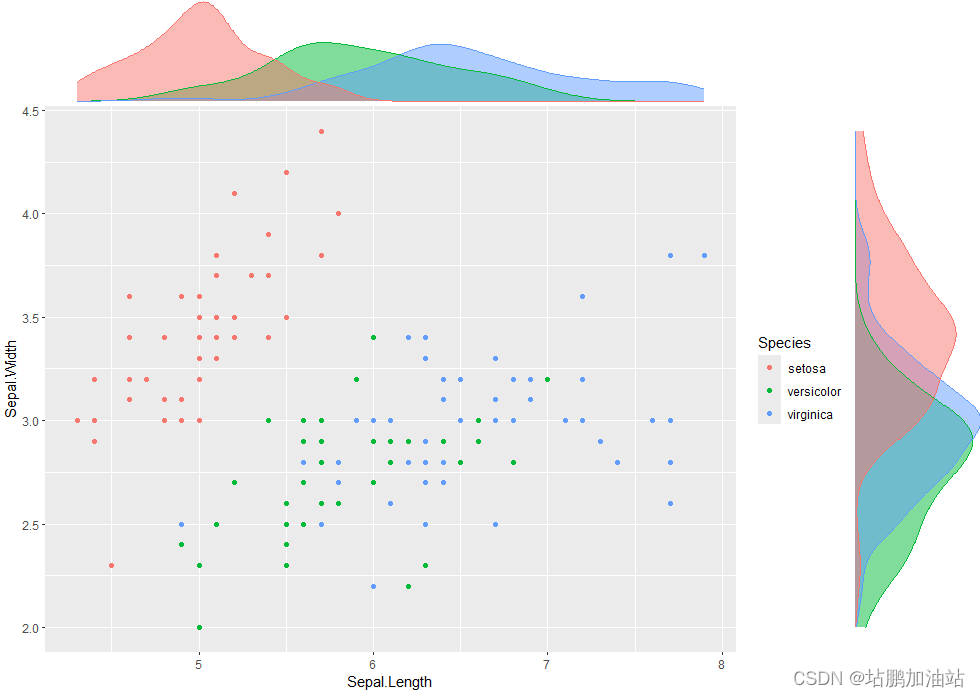 代码如下：

library("ggExtra")
library("ggplot2")

piris <- ggplot(iris, aes(Sepal.Length, Sepal.Width, colour = Species)) +
  geom_point()
ggMarginal(piris, groupColour = TRUE, groupFill = TRUE)

• piris <- ggplot(iris, aes(Sepal.Length, Sepal.Width, colour = Species)) + geom_point()：首先，创建了一个散点图 piris，其中 x 轴表示 Sepal.Length（花萼长度），y 轴表示 Sepal.Width（花萼宽度），并根据 Species（鸢尾花种类）变量进行颜色编码。

• ggMarginal(piris, groupColour = TRUE, groupFill = TRUE)：然后，使用 ggMarginal() 函数对 piris 图进行了包装，以创建带有边际图的散点图。参数 groupColour = TRUE 和 groupFill = TRUE 用于在边际图中反映颜色组。这意味着对于每个不同的鸢尾花种类，都会生成一个单独的边际图，以反映该组中的数据分布情况。

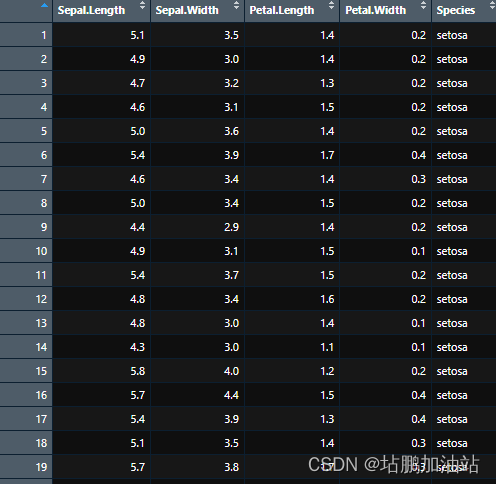
iris的数据集形式如下：