理解一下公钥加密的概念

公钥加密需要一对钥匙,公钥和私钥,公钥可以公开,而私钥不能泄露。

那就可以用公钥给明文加密

而只有私钥才能进行解密

而要想实现这个过程,就需要满足两个点
1:加密简单易行
2:解密困难,这里的困难说的是没有私钥的解密困难
椭圆曲线

先不用管这个公式是如何得到的
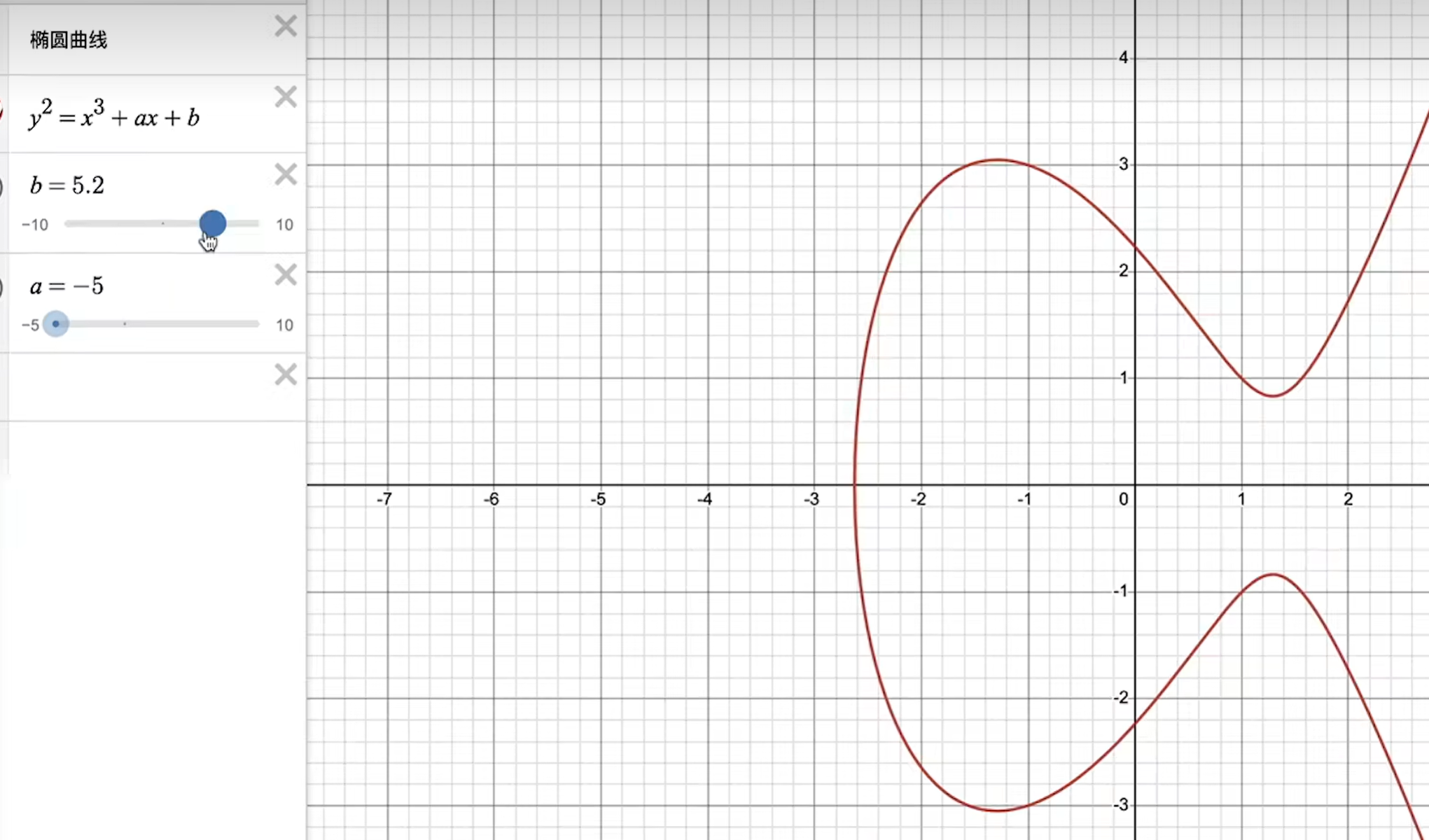
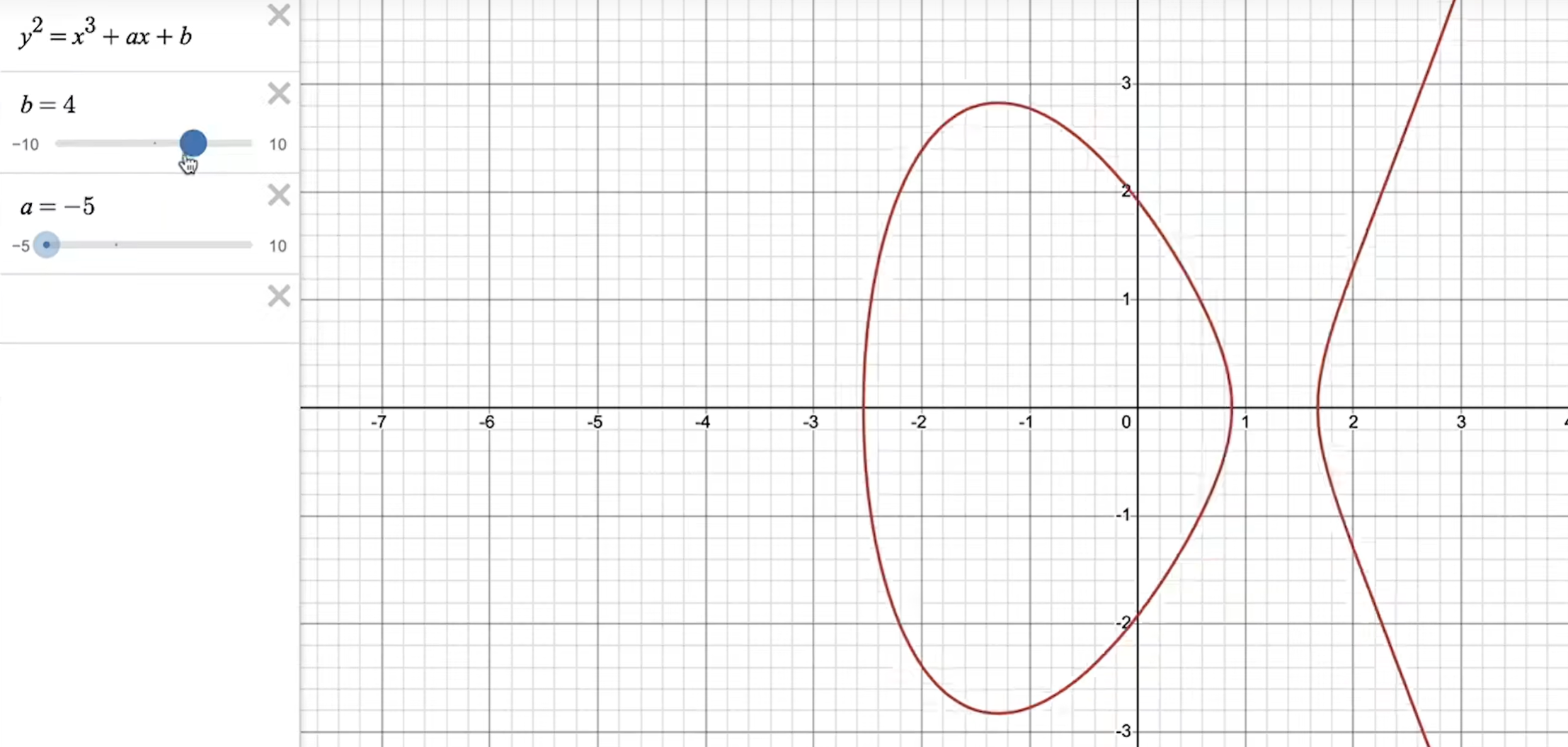
当b的数值发生变化的时候,这里的图形就会也跟着变化,但是图形总体就是一个椭圆和一条曲线,也就是椭圆和曲线的综合体。这也就是椭圆曲线。
分析一下椭圆曲线的特征,观察下面的图片
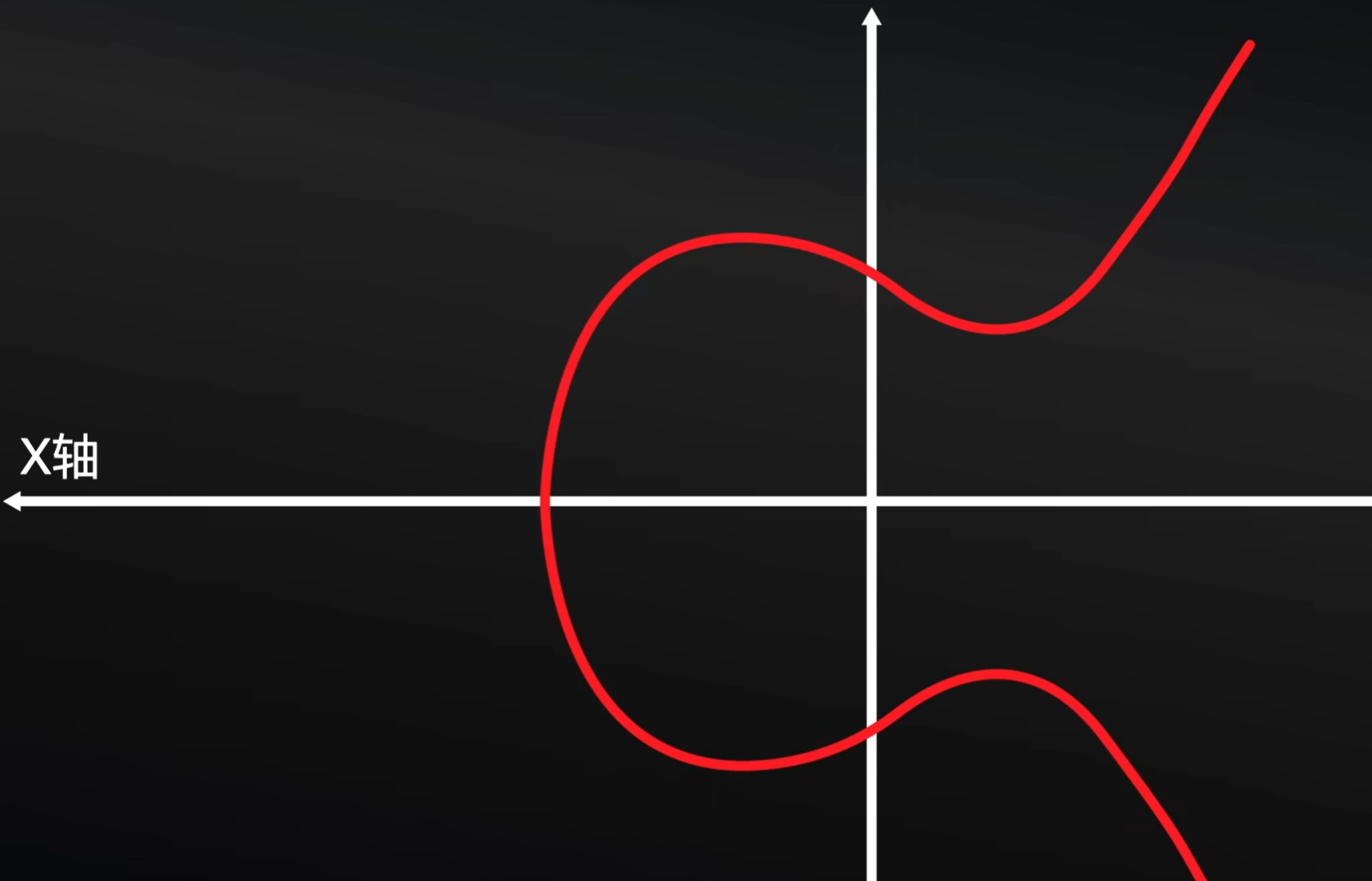
以X轴为中心,对折,我们可以发现,图形线条其实是可以重合的,也就是说。你再上方画一个点,那么下方也一定有一个点是对称的。上下方距离水平线X轴是相同的。
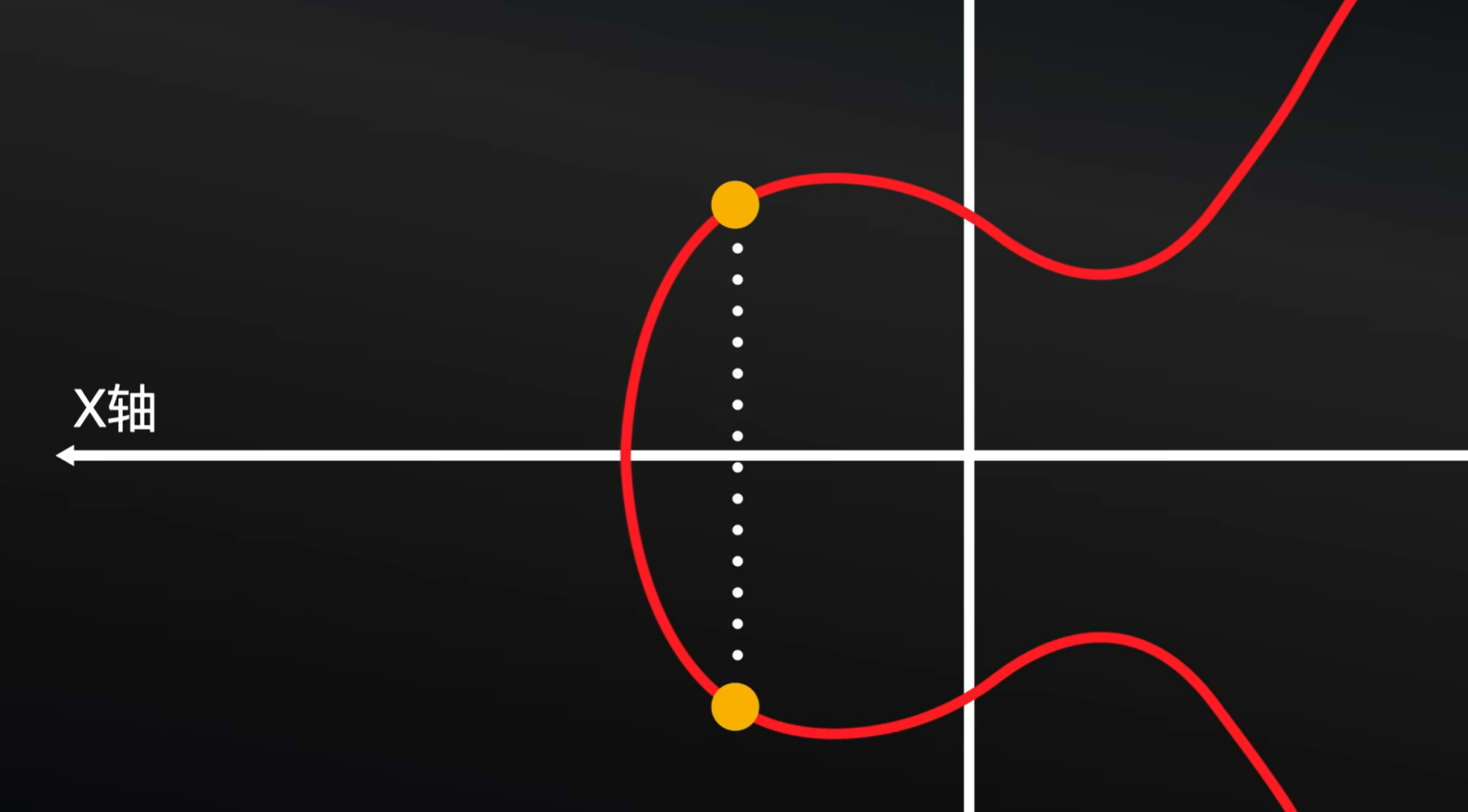
同时,在这个图形上,随便画两个点,而后连线这两个点,形成一条线,延长这条线,这条线就会和图形有第三个交点。当然这里是要求除了垂直线以外的。
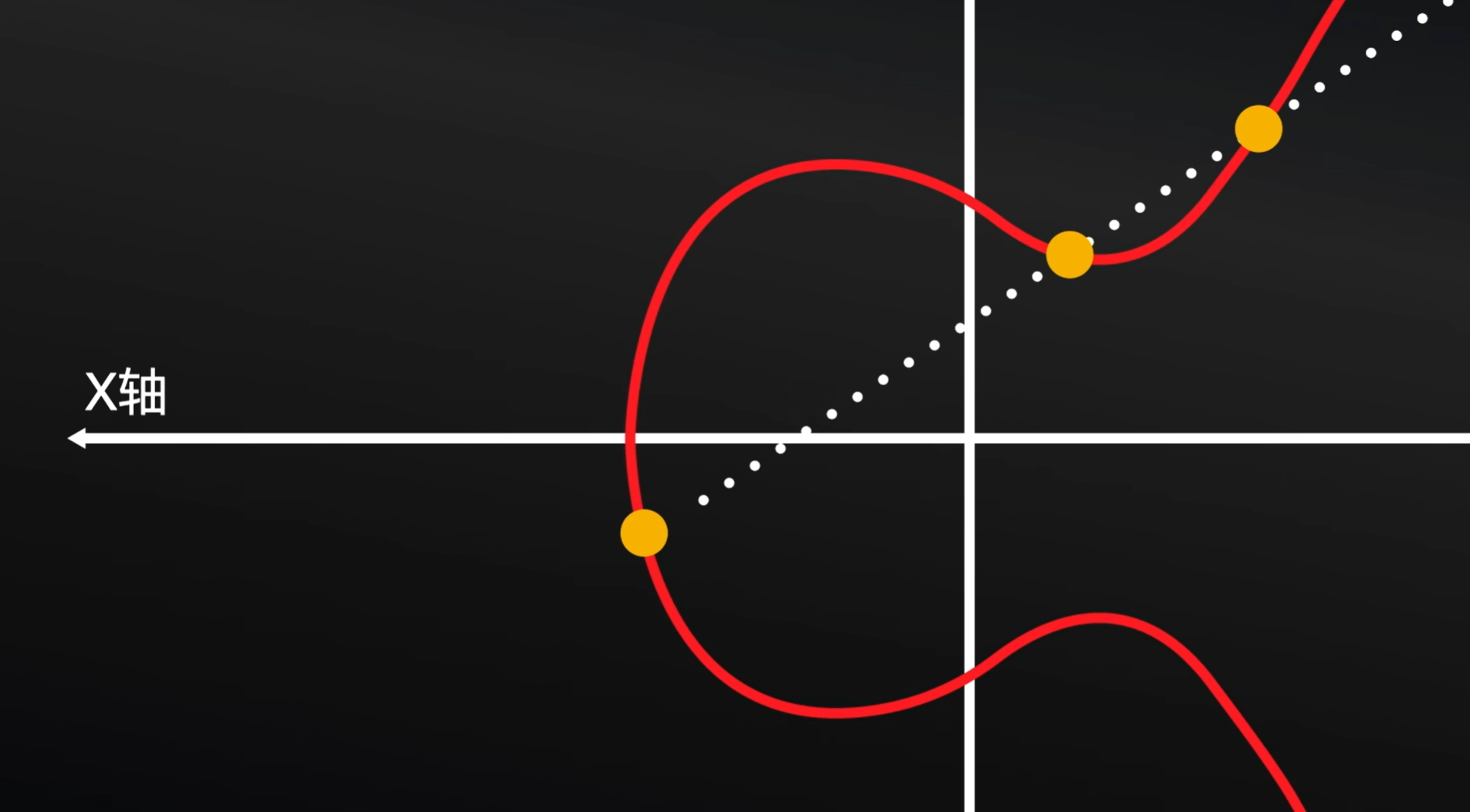
根据以上两个特点,咱们就有的玩了。
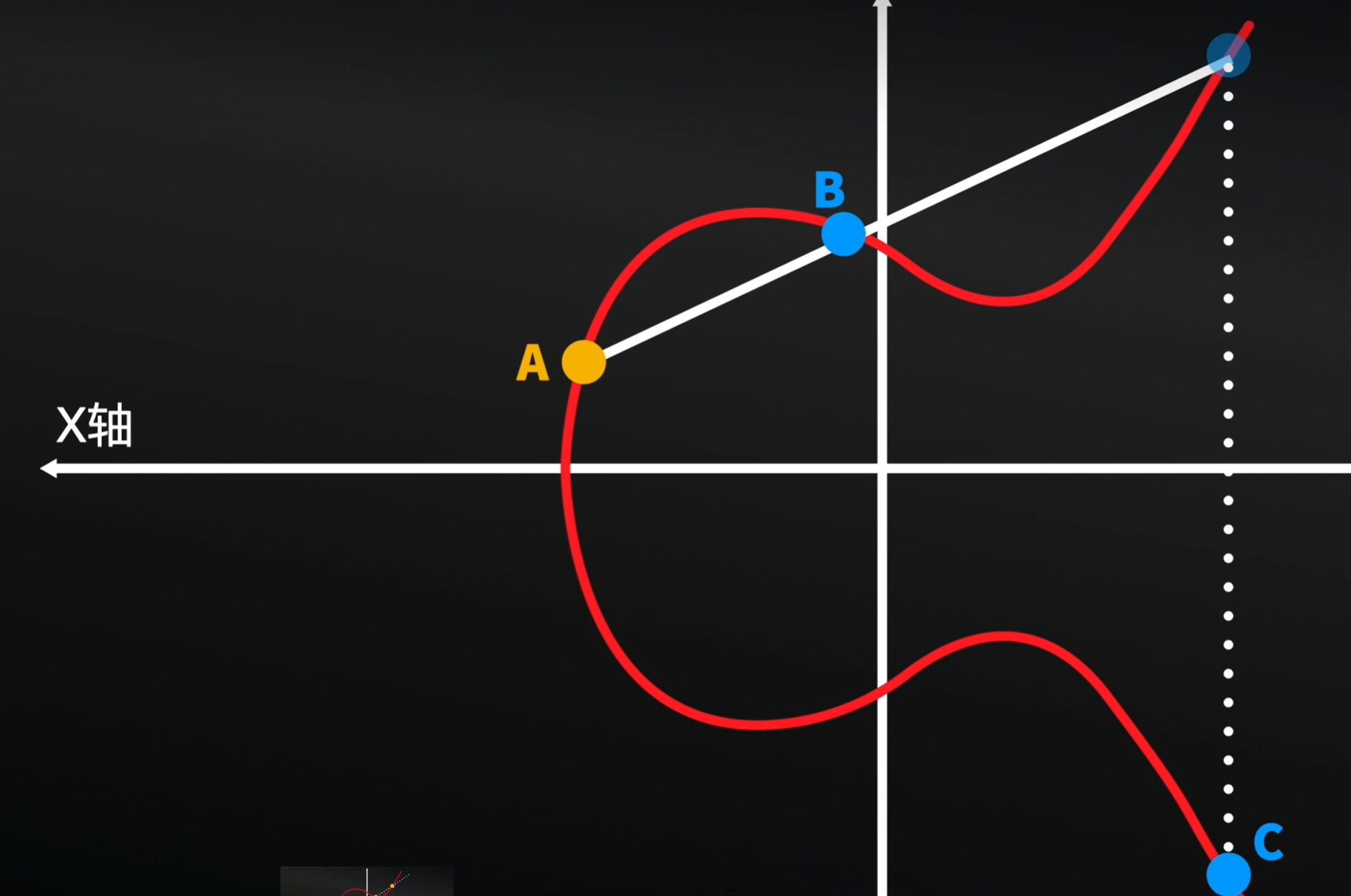
我们在这个图形上随便选择两个点A,B,而后形成一条线以后,延长这个线,形成一个交点,然后再找到这个交点的在这个图形上的对称点。我们将这个点称之为C。
这里我们通过A,B得到C,我们这里就将这个运算称之为点运算,即是:A点B得到C ,这里的点运算其实也就是椭圆曲线上的加法运算。
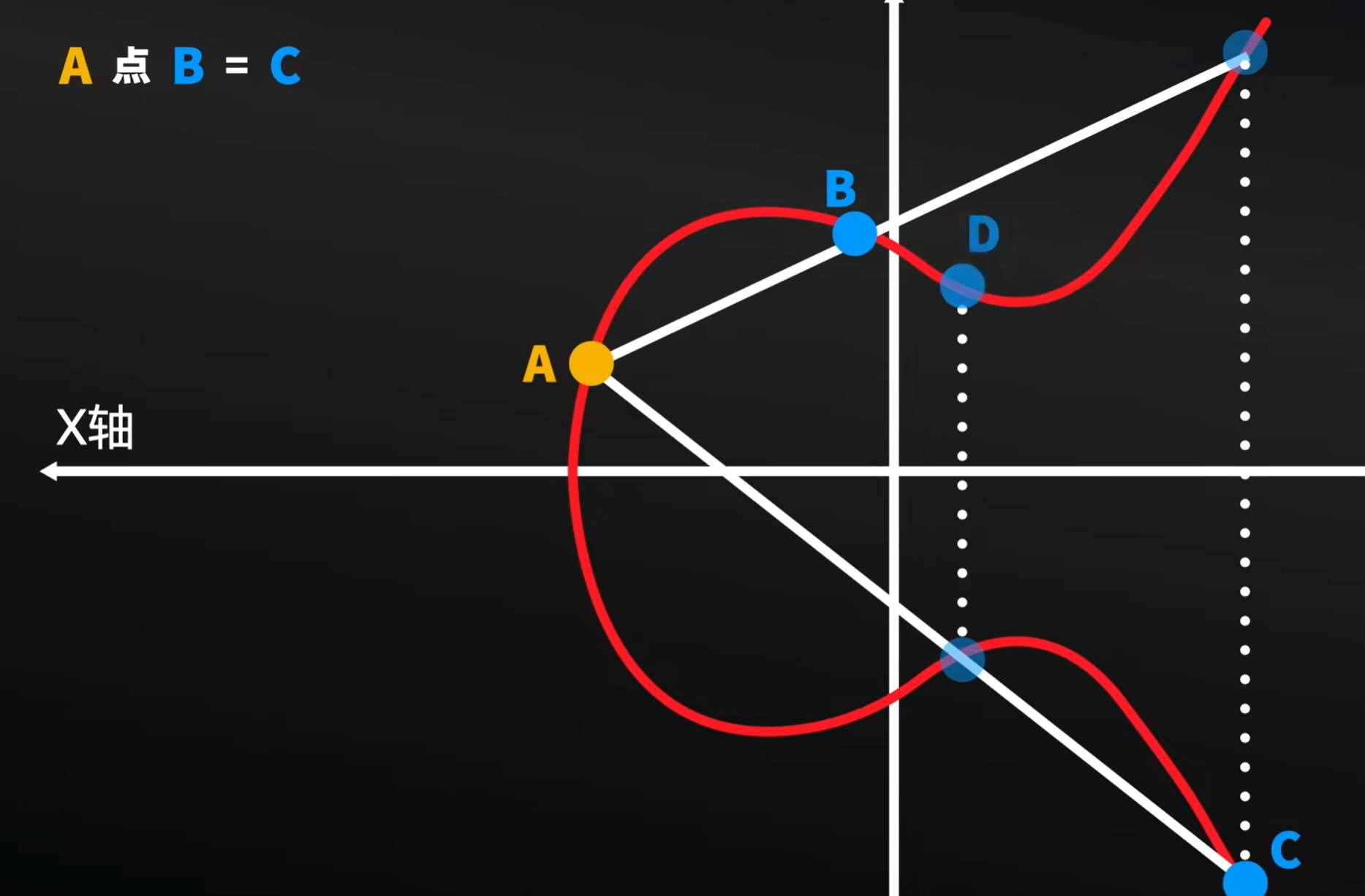
现在我们将A和C进行连线,而这条线也和图形有一个交点,对这个交点找到在图像上的对称点,我们称之为D点。我们就可以称为A点C得到D。
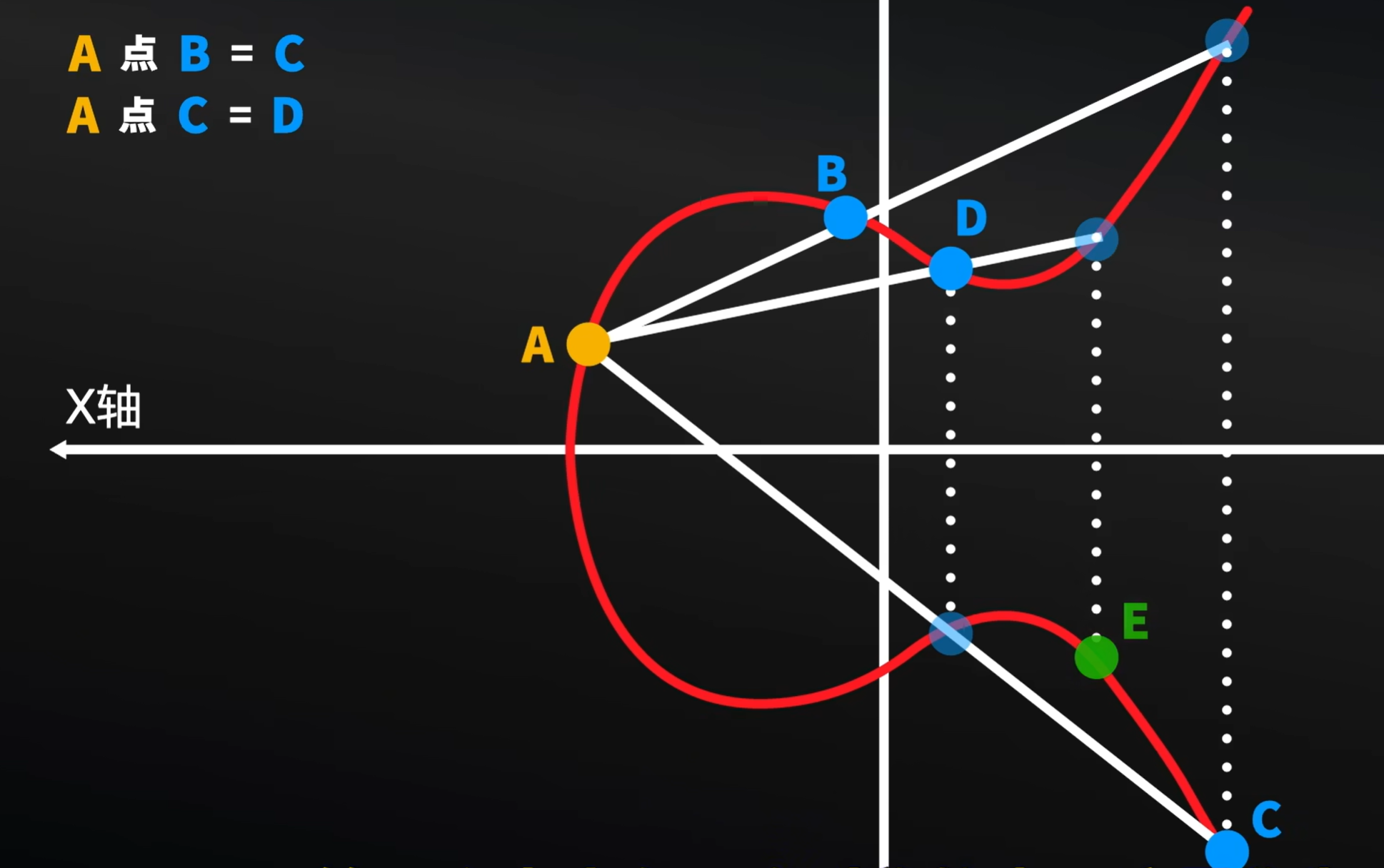
而后A和D连线,形成一条线,与图形交与一点,这个点在图形上的对称点是E,我们称之为A点D得到E。

那么当你们都不知道以上过程的话,问起点A终点是E,请问:经过多少次的点运算得到了E呢?在没有这些线条的时候,大部分人很难知道这个过程。这是很难知道的,同RSA的困难问题。也就符合了前面说的公钥加密的特点:正向简单,而逆向简单。但是用到实际加密过程中,我们还要考虑一种特殊情况。
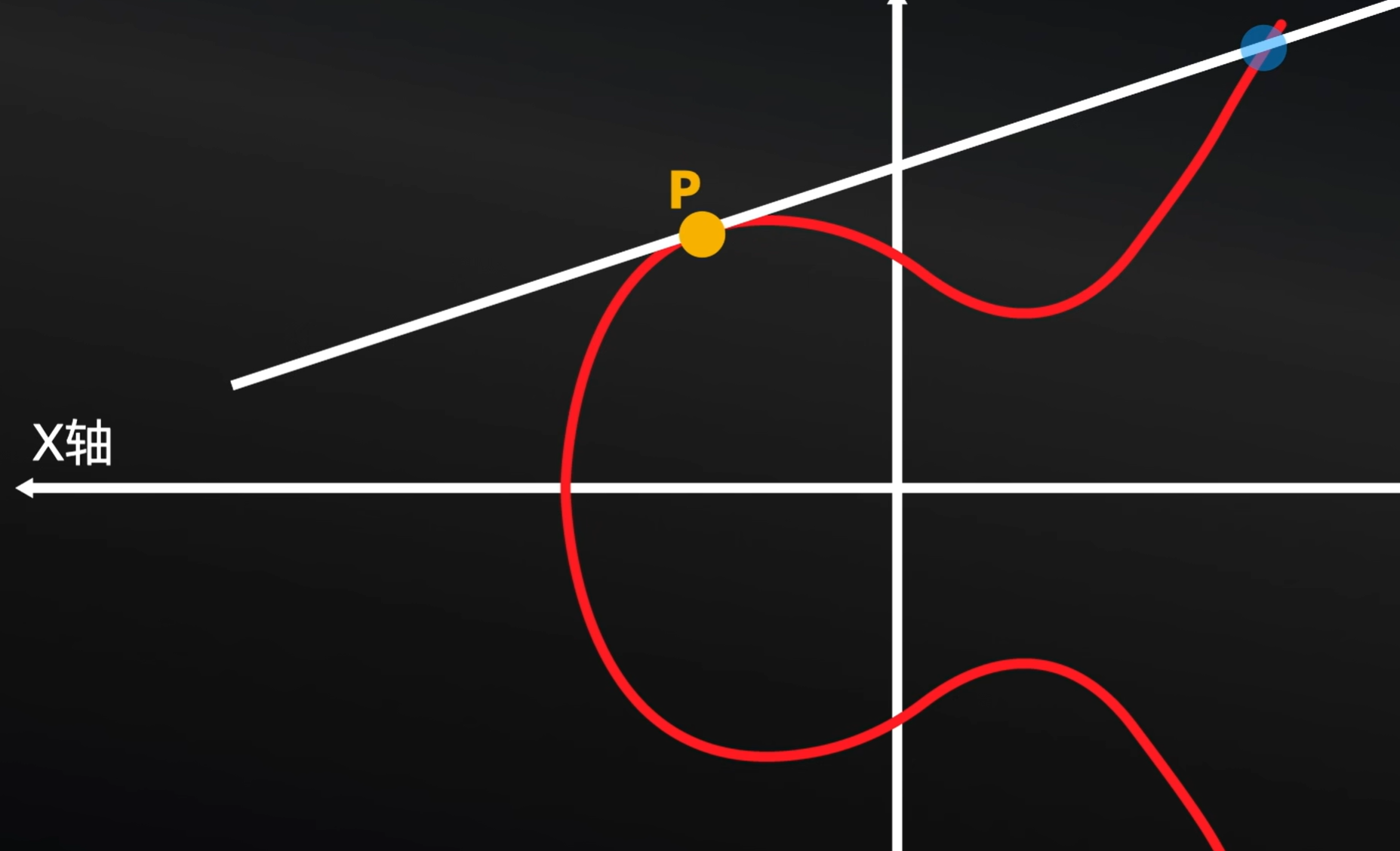
当发生了图中的情况的时候,该如何定义运算呢?这不就是一条切线嘛?
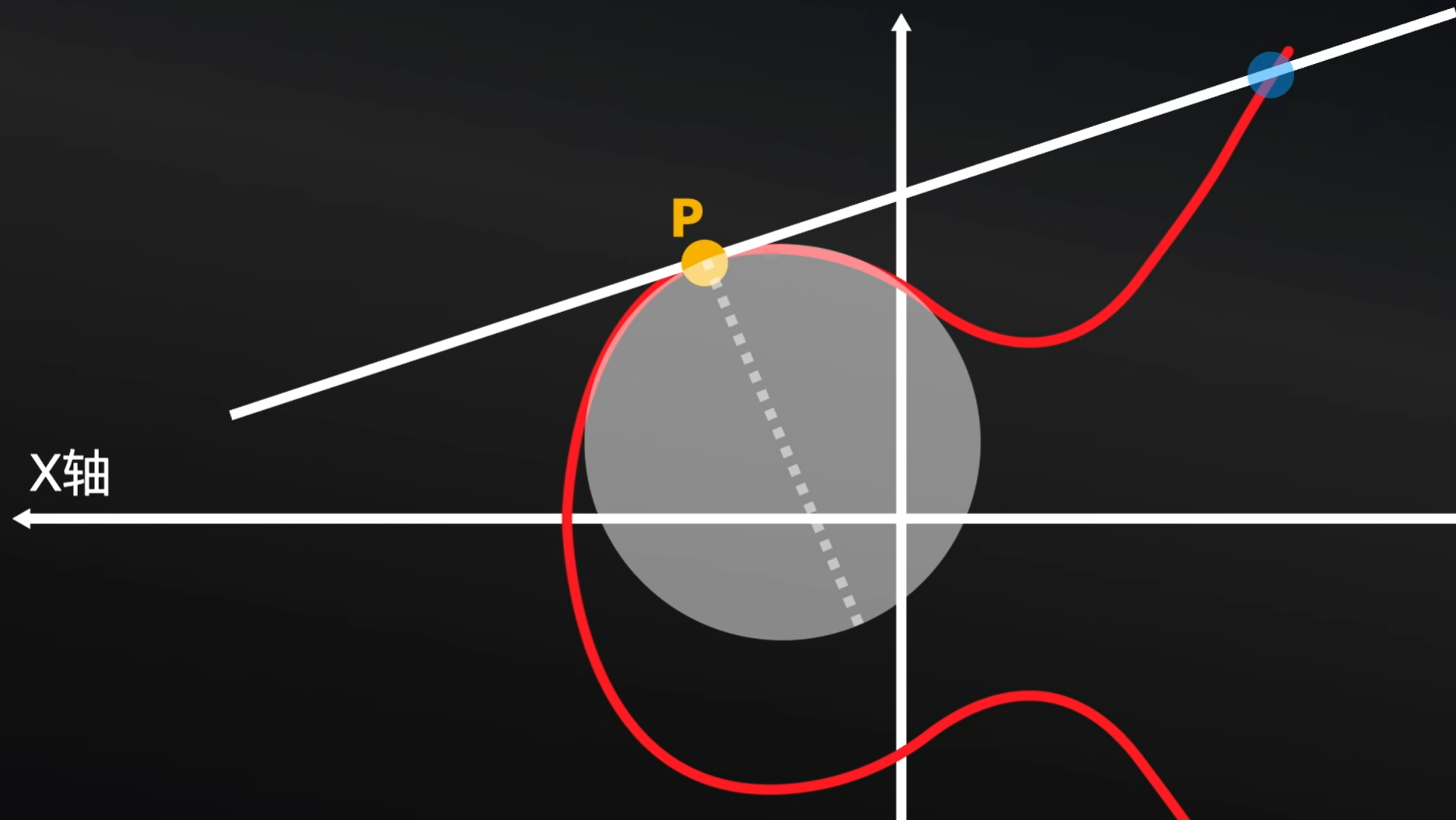
切线垂直于经过切点的半径。
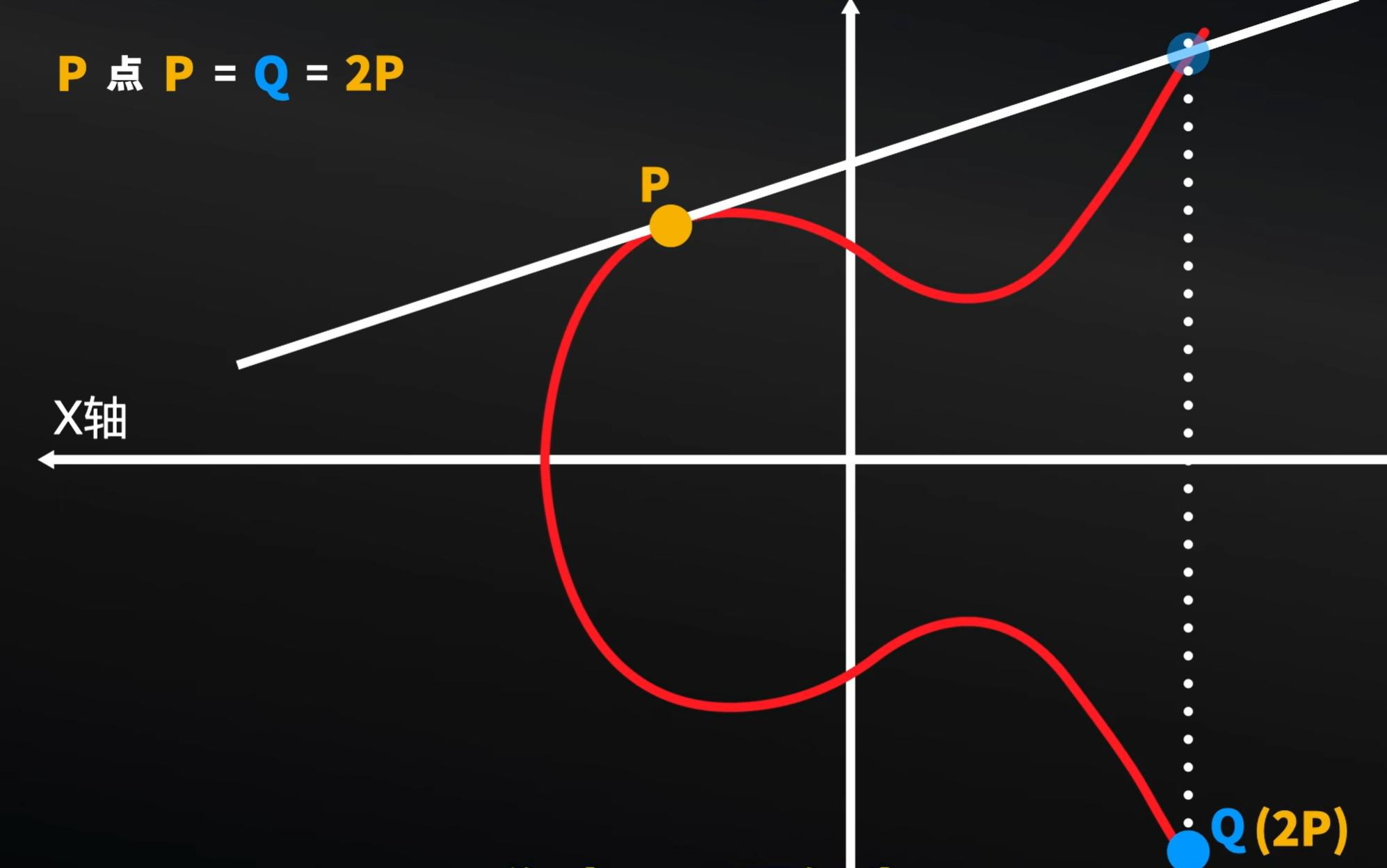
我们将这个情况中,找到延长P后和图像的交点的对称点。我们称之为P点P等于Q.也可以理解为P+P=2P
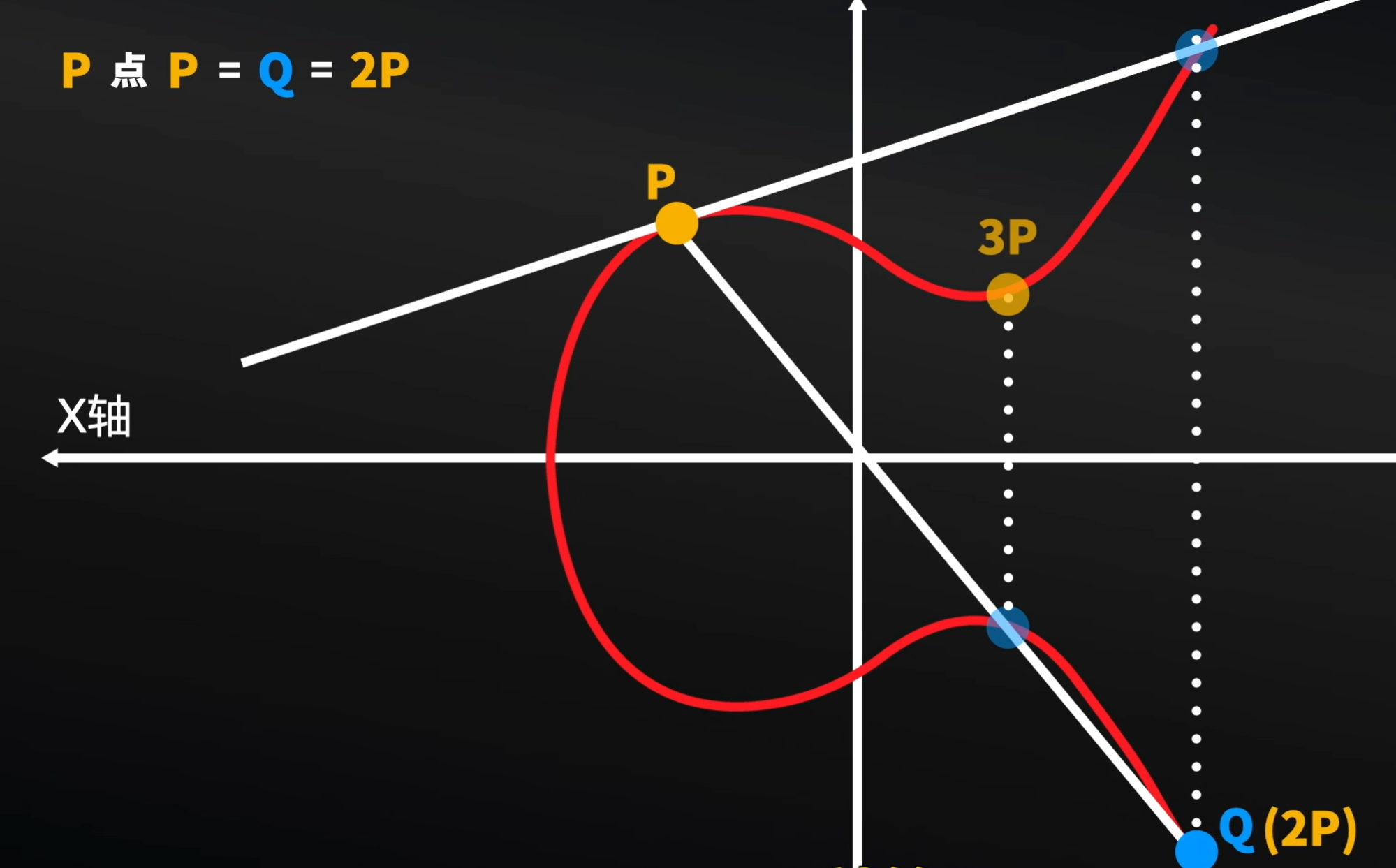
而后P和2P连线,和图形交与一点,这个点在这个图形上也有一个对称的点,我们将之称之为3P
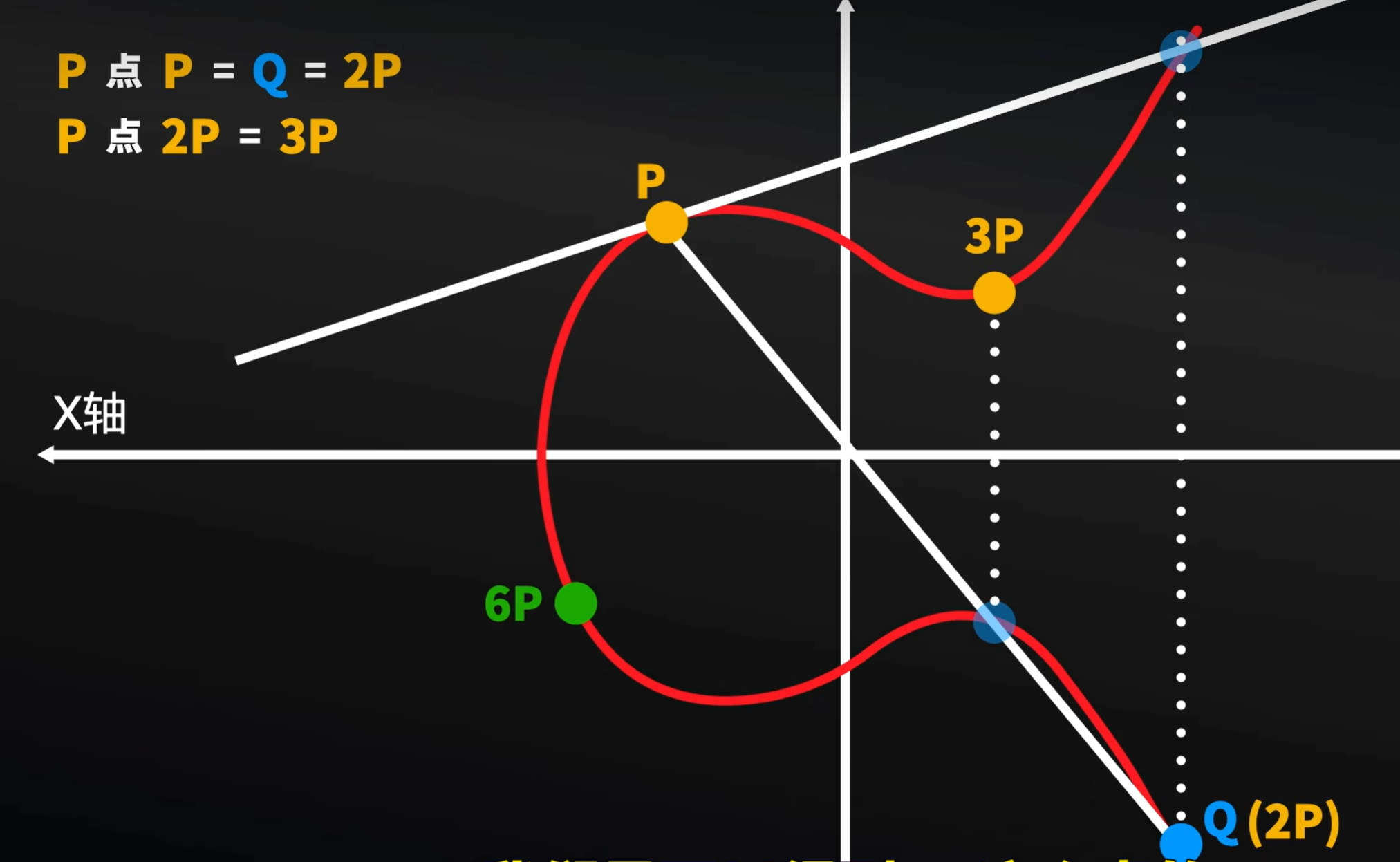
将这个过程延长下去,我们就可以得到6P这个点的。
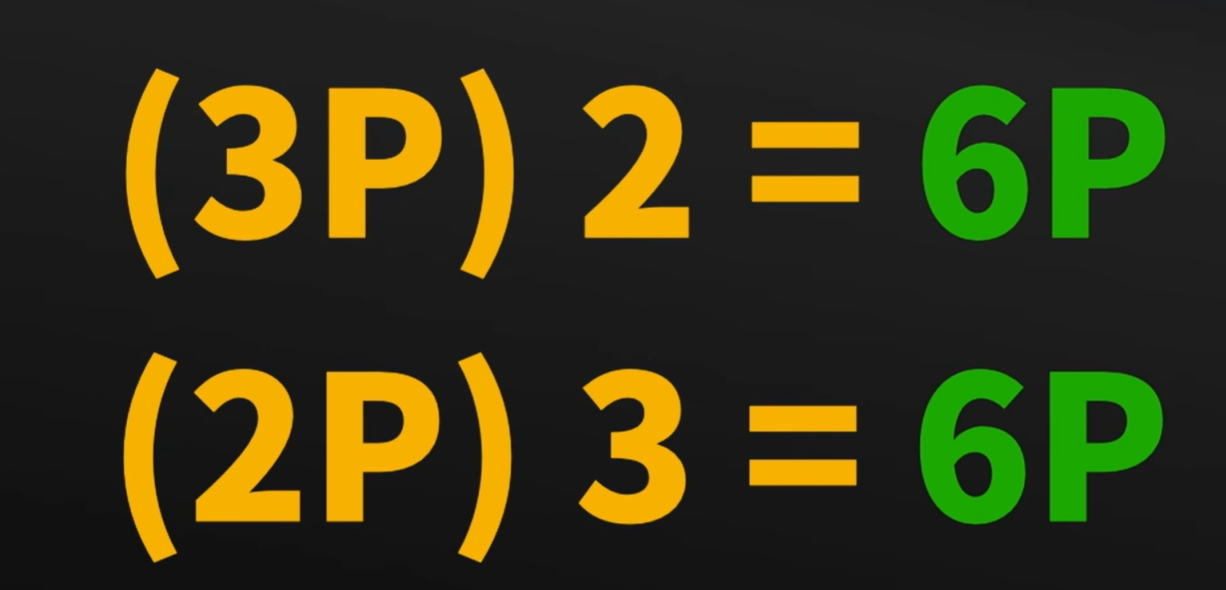
对6P来说,3P点两次可以得到6P,2P点3次也可以得到6P,这就是椭圆曲线上的乘法问题。
ECDHE=椭圆曲线和DH混合起来的算法
复习一下什么是DH算法
Alice和Bob要生成一种只要他们俩才知道的颜色,而Alice有一种私有颜色:青色。Bob也有一种私有的颜色是红色。他俩公开了一种颜色是黄色。Alice用公开的黄色和私有的青色混合到一块生成了一个颜色:绿色,发给Bob。Bob用私有的红色和公开的黄色混合成橙色发给Alice.


Alice将私有的青色和拿到的橙色混合成便便色。Bob将拿到的绿色和私有的红色也混合成便便色。这个颜色就是两者通过交换得到的。而其他人没有这个私有的颜色,很难得到这个颜色。

那么我们就可以将椭圆曲线的特征加到这个DH算法当中。 这也就是我们要讲的ECDHE.
Alice生成一个私钥a,而后再确定生成椭圆上的一个点:G,这个G点是公开的,是大家都知道的G点。Alice要生成一个公钥A,A就通过前面提到的椭圆曲线来计算。即公钥A=aG.
这里就是G这个点进行点运算,次数是a.也就是G点G点G一共进行了a次。得到了椭圆曲线上的一个点A。
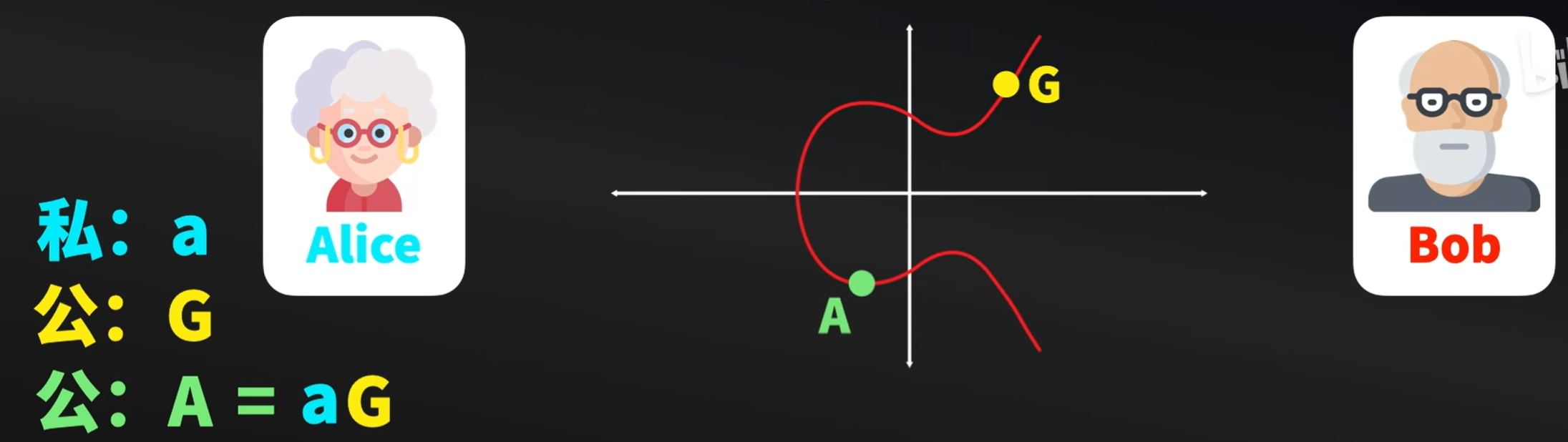
现在Alice把A和G发送给Bob,也是就说A和G是公开的。根据前面的推导,知道A和G推导出a简直难于上青天。知道起点和终点,但是中间经历了多少次,是非常难于计算的。这也就是椭圆曲线加进来的奥妙。
当Bob收到后,也生成了一个私钥b,而后生成椭圆曲线上一个B,B也就是b进行b次点G运算得到的。G点G点G一共进行了b次。Bob将生成的B发给Alice,就算别人知道B和G,也很难知道b
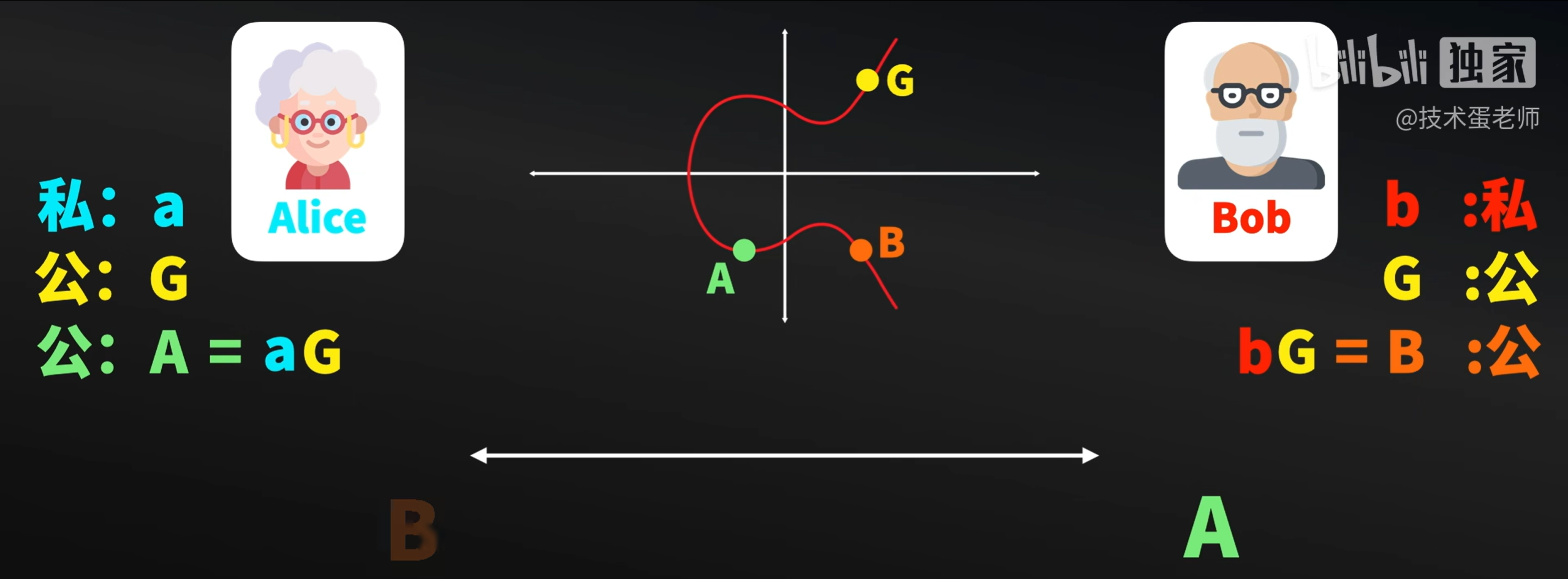
现在Alice将收到的B和a进行运算得到新密钥。Bob用收到的A和b也计算出新的密钥。而这个密钥也就只有他们知道。而且这个密钥是相同的。
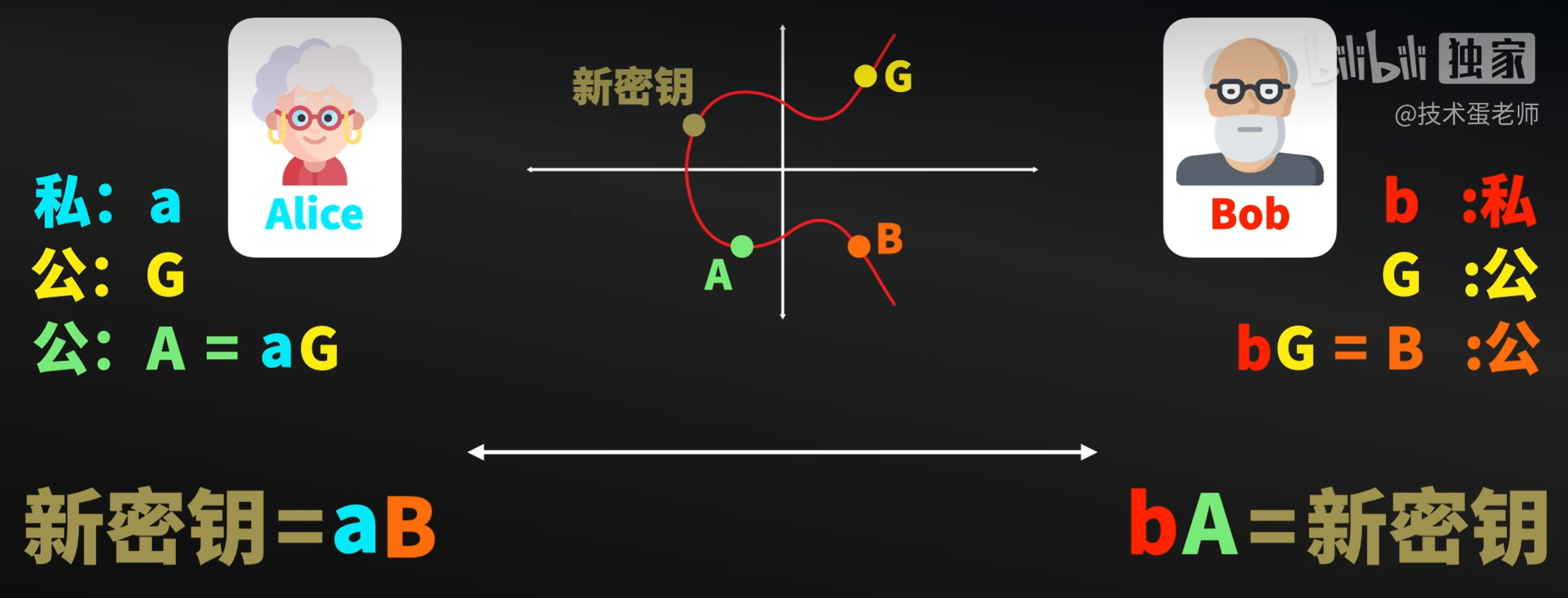
为什么密钥是相同的?在Alice那边有A=aG,而将这个公式带入新密钥=bA中就是baB,Bob也同理。
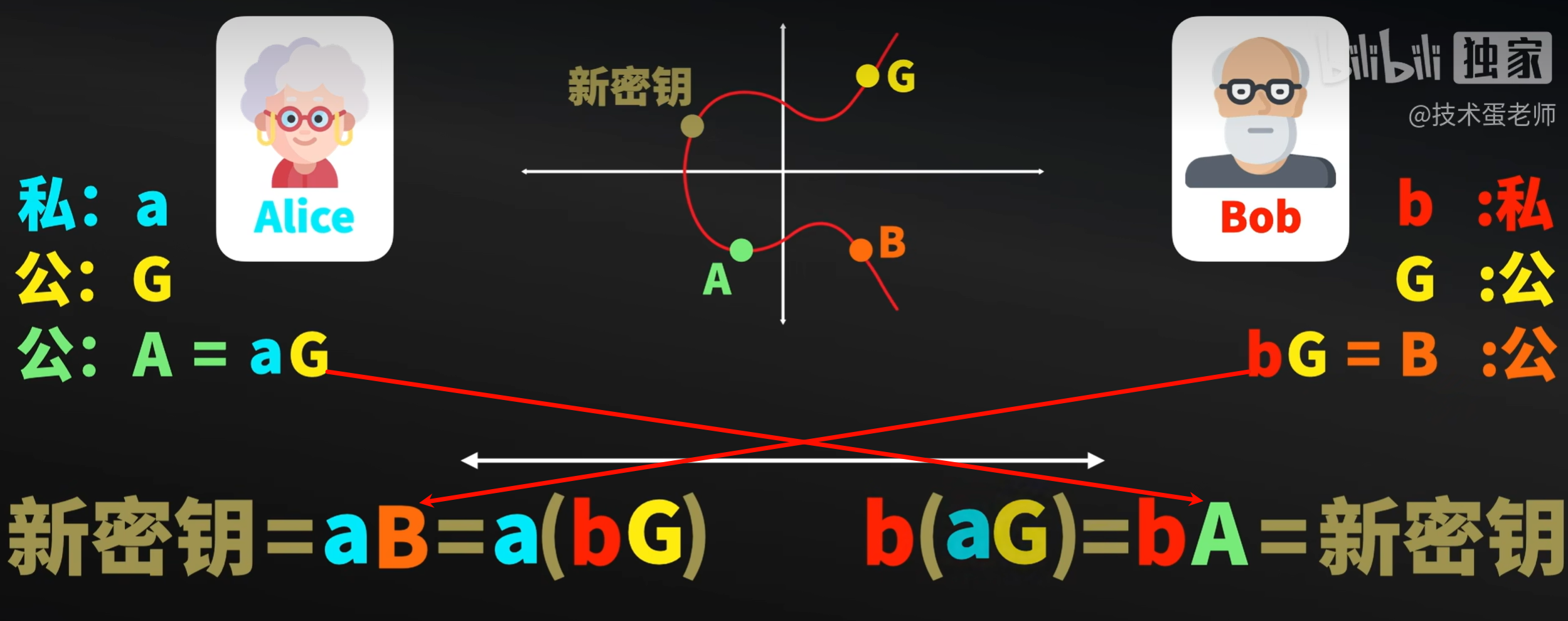
这样一看就知道密钥是相同的,只不过是a和b互换了位置。
优势
和RSA比都是正向简单,逆向困难,但两者中RSA更容易破解。