题目传送门
[PKUSC2018] 星际穿越
简述题意
给定一张 n n n 个点的无向图和 q q q 次询问,每一个点 i i i 与 ∀ j ∈ [ l i , i − 1 ] \forall j \in [l_i , i -1] ∀j∈[li,i−1] 都存在一条长度为 1 1 1 的无向边,每次询问给定 l i , r i , x i l_i,r_i,x_i li,ri,xi,求 1 r i − l i + 1 ∑ y = l i r i d i s t ( x i , y ) \frac{1}{r_i-l_i+1}{\sum_{y=l_i}^{r_i}{dist(x_i,y)}} ri−li+11∑y=liridist(xi,y) 的最简分数形式。
- n , q ≤ 3 × 1 0 5 , 1 ≤ l i < r i < x i ≤ n n,q\leq 3\times 10^5,1\le l_i < r_i < x_i \le n n,q≤3×105,1≤li<ri<xi≤n
思路
Subtask1 & 2
直接把图建出来,对每一个点暴力跑一遍
dijkstra
\text{dijkstra}
dijkstra,每次询问累和即可。
时间复杂度
O
(
n
2
l
o
g
n
)
O(n^2logn)
O(n2logn),可以得到
45
p
t
s
45pts
45pts。
Subtask3
与正解强相关!
先把图降维成序列问题,把 n n n 个点抽象成 n n n 个元素的序列 a a a。
考虑贪心,由于
l
i
<
r
i
<
x
i
l_i < r_i < x_i
li<ri<xi,因此一定尽可能往右跳,才能最小化步数。
不妨令
n
x
t
i
,
j
nxt_{i,j}
nxti,j 表示从
i
i
i 开始跳
j
j
j 步,能到达的最小点。
显然 n x t i , 0 = l i nxt_{i,0} = l_i nxti,0=li,然而 n x t i , 1 nxt_{i,1} nxti,1 一定等于 l l x i l_{l_{x_i}} llxi 嘛?
不是。如果有一个点 j ∈ [ l x i , i − 1 ] j \in [l_{x_i},i-1] j∈[lxi,i−1] 满足 l j ≤ l l x i l_j \le l_{l_{x_i}} lj≤llxi,那么跳到 j j j 一定比跳到 l x i l_{x_i} lxi 更优,因此有:
n x t i , j = min { l n x t i , j − 1 , . . . , l i − 1 , l i , l i + 1 , . . . , l n } nxt_{i,j}=\min\{l_{nxt_{i,j-1}},...,l_{i-1},l_i,l_{i+1},...,l_n\} nxti,j=min{lnxti,j−1,...,li−1,li,li+1,...,ln}
为什么要考虑
[
i
+
1
,
n
]
[i+1,n]
[i+1,n] 这一部分呢?因为有可能往右跳比往左跳更优,举个例子可能更形象:
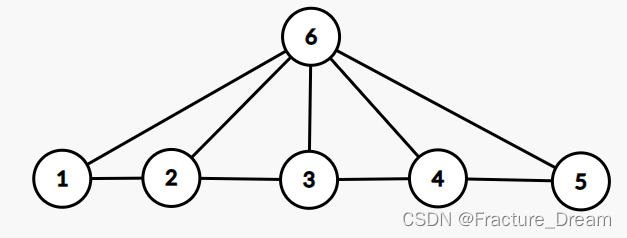
假如 5 5 5 是起点, 1 1 1 是终点,那么很显然 5 → 6 5 \rightarrow 6 5→6 比 5 → 4 5 \rightarrow 4 5→4 更优。
因此枚举每个点作为起点,进行一次上述过程即可。
最坏时间复杂度
O
(
n
2
)
O(n^2)
O(n2),可以得到
75
p
t
s
75pts
75pts。
Subtask4
上述做法中,发现我们的时间复杂度瓶颈在于 j j j 这一维,而且正解时间复杂度应该是 O ( n l o g n ) O(nlogn) O(nlogn),这都启发我们倍增。
不妨令 d p i , j dp_{i,j} dpi,j 表示从 i i i 开始跳 2 j 2^j 2j 步能够到达的最小点。
那么有经典倍增式 d p i , j = d p d p i , j − 1 , j − 1 dp_{i,j} = dp_{dp_{i,j-1},j-1} dpi,j=dpdpi,j−1,j−1。
然后显然有
d
p
i
,
0
=
l
i
dp_{i,0}=l_i
dpi,0=li?大多数人的第一想法可能都是这样初始化,然而这显然是错的!
再举个例子。
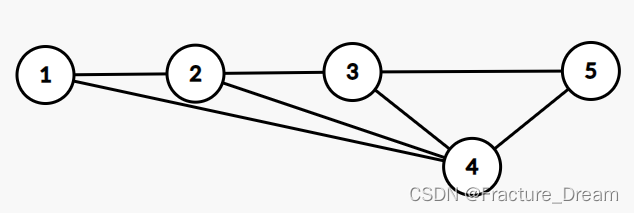
如上图,如果这样初始化就有
d
p
5
,
1
=
d
p
d
p
5
,
0
,
0
=
d
p
3
,
0
=
2
dp_{5,1}=dp_{dp_{5,0},0}=dp_{3,0}=2
dp5,1=dpdp5,0,0=dp3,0=2,然而显然可以
5
→
4
→
1
5 \rightarrow 4 \rightarrow 1
5→4→1,为什么会出错呢?由
subtask3
\text{subtask3}
subtask3 的做法可得,我们没有考虑往右跳的情况。
然而每个点都会出现往右跳的情况吗?
显然不是。具体地,有如下引理:
引理:
在任意最优情形下,只有起点可能往右跳,其他点一定只会向左跳。
证明也是显然的,如果当前点往右跳到 x x x 更优,那为何不直接从上一个点(一定会有前驱点)跳到 x x x 呢?
因此,我们只需要考虑起点往右跳的情况,就可以保证递推的重要性,因此 d p i , 0 = min { l i , l i + 1 , . . . , l n } dp_{i,0}=\min\{l_i,l_{i+1},...,l_n\} dpi,0=min{li,li+1,...,ln}(至于那些 i i i 往右跳无法到达的点一定有 l j > i l_{j} > i lj>i,所以考虑了也无所谓),发现这样初始化代入上述例子也是对的。
考虑如何回答询问。不妨令
s
u
m
i
,
j
sum_{i,j}
sumi,j 表示
i
i
i 到
[
d
p
i
,
j
,
i
−
1
]
[dp_{i,j},i-1]
[dpi,j,i−1] 的距离和。
那么有
s
u
m
i
,
0
=
i
−
d
p
i
,
0
sum_{i,0}=i-dp_{i,0}
sumi,0=i−dpi,0。
- 先考虑 [ d p i , j − 1 , i − 1 ] [dp_{i,j-1},i-1] [dpi,j−1,i−1] 这一部分的贡献,即 s u m i , j − 1 sum_{i,j-1} sumi,j−1。
- 再考虑 [ d p i , j , d p i , j − 1 − 1 ] [dp_{i,j},dp_{i,j-1}-1] [dpi,j,dpi,j−1−1] 这一部分的贡献,我们已知从 d p i , j − 1 dp_{i,j-1} dpi,j−1 这个点走到这些点的距离,即为 s u m d p i , j − 1 , j − 1 sum_{dp_{i,j-1},j-1} sumdpi,j−1,j−1,所以只需要从 i i i 走 2 j − 1 2^{j-1} 2j−1 到 d p i , j − 1 dp_{i,j-1} dpi,j−1,一共要走 d p i , j − 1 − d p i , j dp_{i,j-1}-dp_{i,j} dpi,j−1−dpi,j 次。
总结一下有:
s
u
m
i
,
j
=
s
u
m
i
,
j
−
1
+
s
u
m
d
p
i
,
j
−
1
,
j
−
1
+
2
j
−
1
×
(
d
p
i
,
j
−
1
−
d
p
i
,
j
)
sum_{i,j}=sum_{i,j-1}+sum_{dp_{i,j-1},j-1}+2^{j-1}\times(dp_{i,j-1}-dp_{i,j})
sumi,j=sumi,j−1+sumdpi,j−1,j−1+2j−1×(dpi,j−1−dpi,j)
注意,在上述推导过程中,我们并未考虑从起点往右跳的贡献,这一部分会在后文详细阐述。
求得 d p , s u m dp,sum dp,sum 以后,即可处理询问:
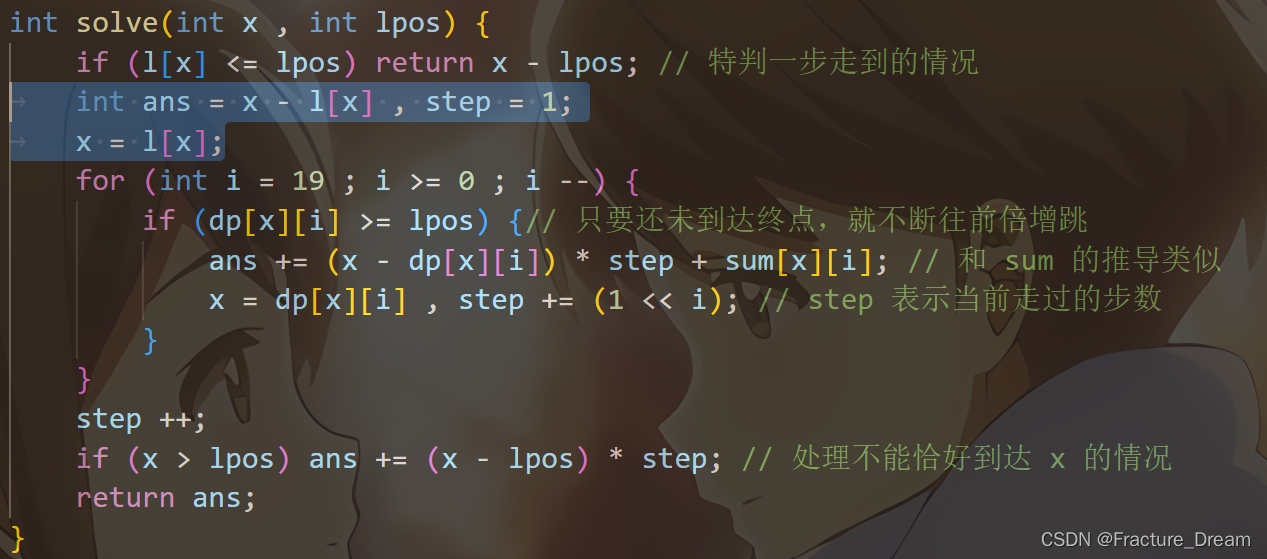
该函数旨在求出求出
x
x
x 走到
[
l
p
o
s
,
x
−
1
]
[lpos, x-1]
[lpos,x−1] 的距离和。
有注释的部分应该很好理解,瓶颈在于框出的两行代码,网上大多数题解这一部分都没有写明白。
为什么要强制走到 l x l_x lx 呢?注意到,我们之前 s u m sum sum 的推导并没有考虑 x x x 最开始往右跳的贡献,所以我们要强制选择一个点,那么为什么选择了 l i l_i li 呢?
- 如果 x x x 最开始向右跳到 y y y 更优,那么从 l x l_x lx 出发可以且一定会跳到 y y y,就等价于 x x x 跳到 y y y,区别在于 l x l_x lx 出发可以顺便处理这一部分的贡献。
- 如果 x x x 最开始向左跳到 x x x 更优,同理,从 l x l_x lx 出发也一定会跳到 y y y。
通俗的讲,先强制选择
l
x
l_x
lx 其作用就在于等着被替代成其他点。表面上从
x
x
x 跳到了
l
x
l_x
lx,实际是从
x
x
x 跳到了
y
y
y。
即
x
→
l
x
→
y
x \rightarrow l_x \rightarrow y
x→lx→y 等价于
x
→
y
x \rightarrow y
x→y,但前者可以处理向右跳的贡献。
结合样例可以更好理解。
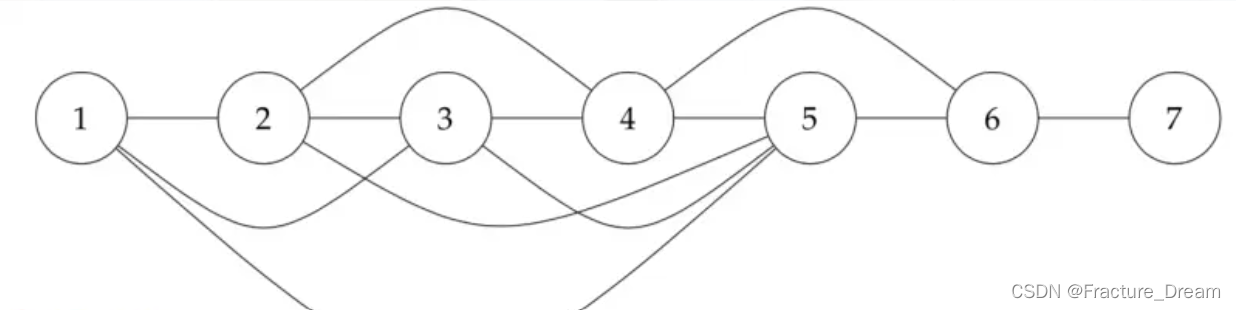
如果 6 6 6 为起点,那么我们会强制跳到 4 4 4,表面上错过了可以直达 1 1 1 的 5 5 5,但是 4 4 4 是可以且一定会向右跳到 5 5 5 的,因为我们的倍增是最优的。
代码
一道非常好的倍增题!!!
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN = 3e5 + 5;
int n , q , dp[MAXN][20] , sum[MAXN][20] , l[MAXN];
int solve(int x , int lpos) { // 求出 x 走到 [lpos , x-1] 的距离和
if (l[x] <= lpos) return x - lpos; // 特判一步走到的情况
int ans = x - l[x] , step = 1;
x = l[x];
for (int i = 19 ; i >= 0 ; i --) {
if (dp[x][i] >= lpos) {// 只要还未到达终点,就不断往前倍增跳
ans += (x - dp[x][i]) * step + sum[x][i]; // 和 sum 的推导类似
x = dp[x][i] , step += (1 << i); // step 表示当前走过的步数
}
}
step ++;
if (x > lpos) ans += (x - lpos) * step; // 处理不能恰好到达 x 的情况
return ans;
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr) , cout.tie(nullptr);
cin >> n;
for (int i = 2 ; i <= n ; i ++) cin >> l[i] , dp[i][0] = l[i];
for (int i = n - 1 ; i >= 2 ; i --) dp[i][0] = min(dp[i + 1][0] , dp[i][0]);
for (int i = 1 ; i <= n ; i ++) sum[i][0] = i - dp[i][0];
for (int j = 1 ; j <= 19 ; j ++) {
for (int i = 2 ; i <= n ; i ++) {
dp[i][j] = dp[dp[i][j - 1]][j - 1];
sum[i][j] = sum[i][j - 1] + sum[dp[i][j - 1]][j - 1] + (dp[i][j - 1] - dp[i][j]) * (1 << j - 1);
}
}
cin >> q;
while(q --) {
int ql , qr , x;
cin >> ql >> qr >> x;
int div = (qr - ql + 1) , w = solve(x , ql) - solve(x , qr + 1);
int g = __gcd(div , w);
w /= g , div /= g; // 约分
cout << w << '/' << div << '\n';
}
return 0;
}