在数据结构的学习中,队列是一种常用的线性数据结构,它遵循先进先出(FIFO)的原则。而单调队列是队列的一种变体,它在特定条件下保证了队列中的元素具有某种单调性质,例如单调递增或单调递减。单调队列在处理一些特定问题时非常有用,比如滑动窗口的单调性问题。
单调队列所解决的问题
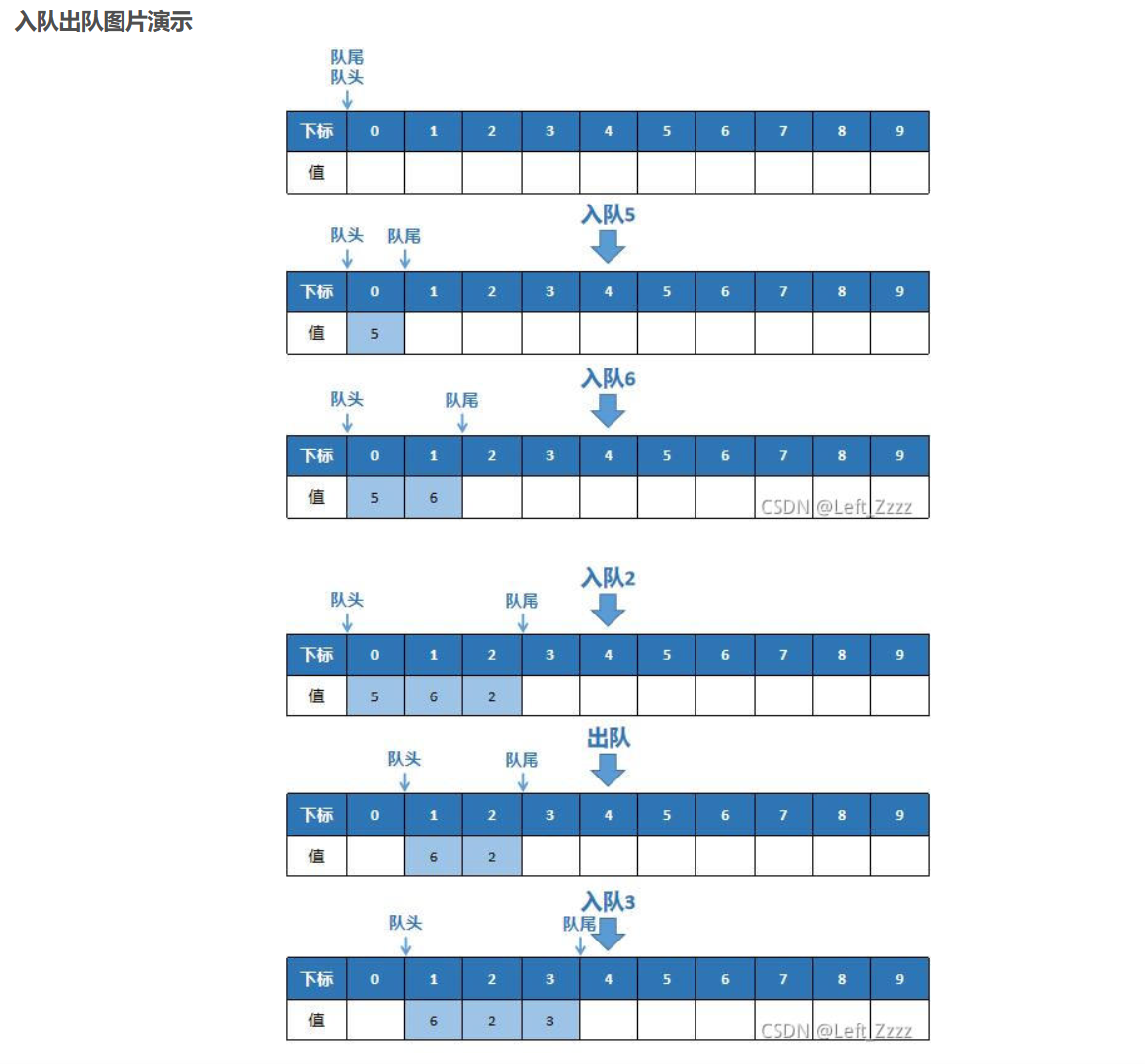
单调队列主要是为了求滑动窗口最大/最小值。单调队列是双端队列(首尾两边都可以append和pop)。具体而言,我们会在单调队列的队尾pop和append,会在队首pop
滑动窗口:只能左边界L向右移动或不动、右边界R向右移动或不动,二者不能向左移动。
基本概念
单调队列的类型:
从头到尾递减:可以求滑动窗口内的最大值
从头到尾递增:可以求滑动窗口内的最小值
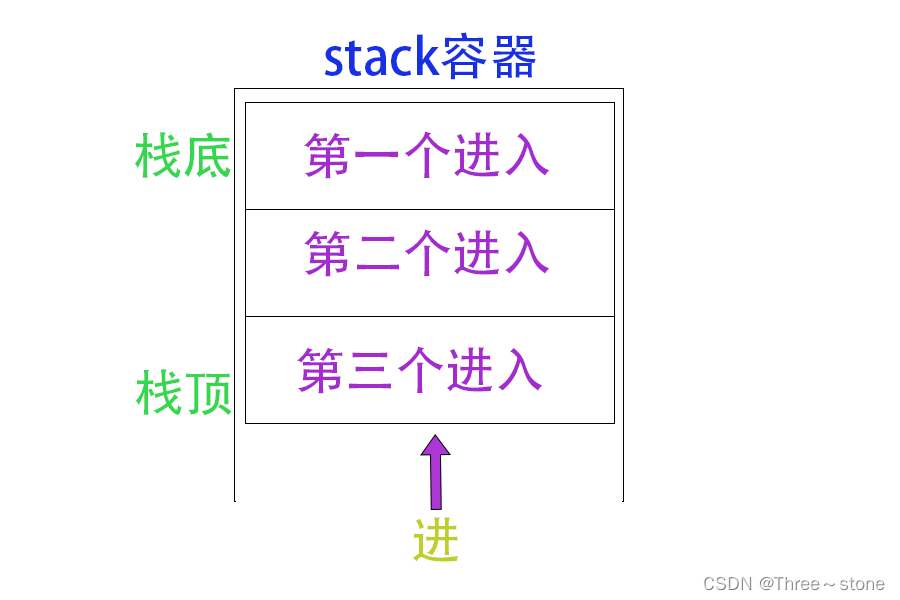
我们之前学过单调栈:

由上图可以看出,对于栈内元素来说:
- 在栈内左边的数就是数组中左边第一个比自己小的元素;
- 但元素被弹出时,遇到的就是数组中右边第一个比自己小的元素。
对于将要入栈的元素来说:在对栈进行更新后(即弹出了所有比自己大的元素),此时栈顶元素就是数组中左侧第一个比自己小的元素;
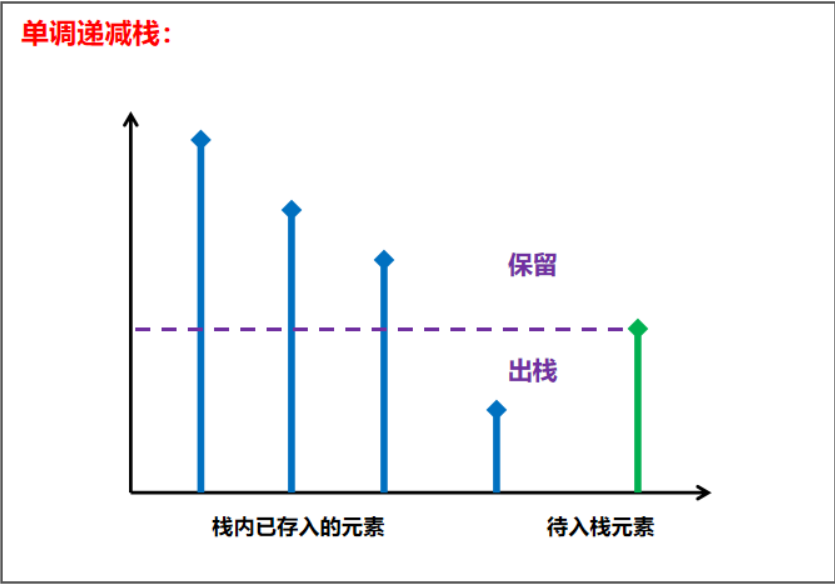
由上图可以看出,对于栈内元素来说:
- 在栈内左边的数就是数组中左边第一个比自己大的元素;
- 但元素被弹出时,遇到的就是数组中右边第一个比自己大的元素。
对于将要入栈的元素来说:在对栈进行更新后(即弹出了所有比自己小的元素),此时栈顶元素就是数组中左侧第一个比自己大的元素;
!!!!!!!!!!!!!!单调队列在这里的操作其实是和单调栈差不多的!!!!!!!!!!
为什么要选择这样的单调性:
首先规定队首的元素是我们需要的最值(这一点非常重要),所以递减队列的队首是最大值,递增队列的队首是最小值。其次我们从下面对队列中元素的理解也可以看到。从队首到队尾的元素成为所需最值的优先级需要依次递减。
在单调队列中,头和尾都可以pop,但只有尾可以append。
特别注意:单调队列里存放的是index(下标)而不是元素值(其实也可以是(value, index)这种),这是因为我们无法用元素值来判断元素是否过期。但是我们在谈论元素大小时,指的不是index的大小,而是index在原数组对应value的大小。
用法
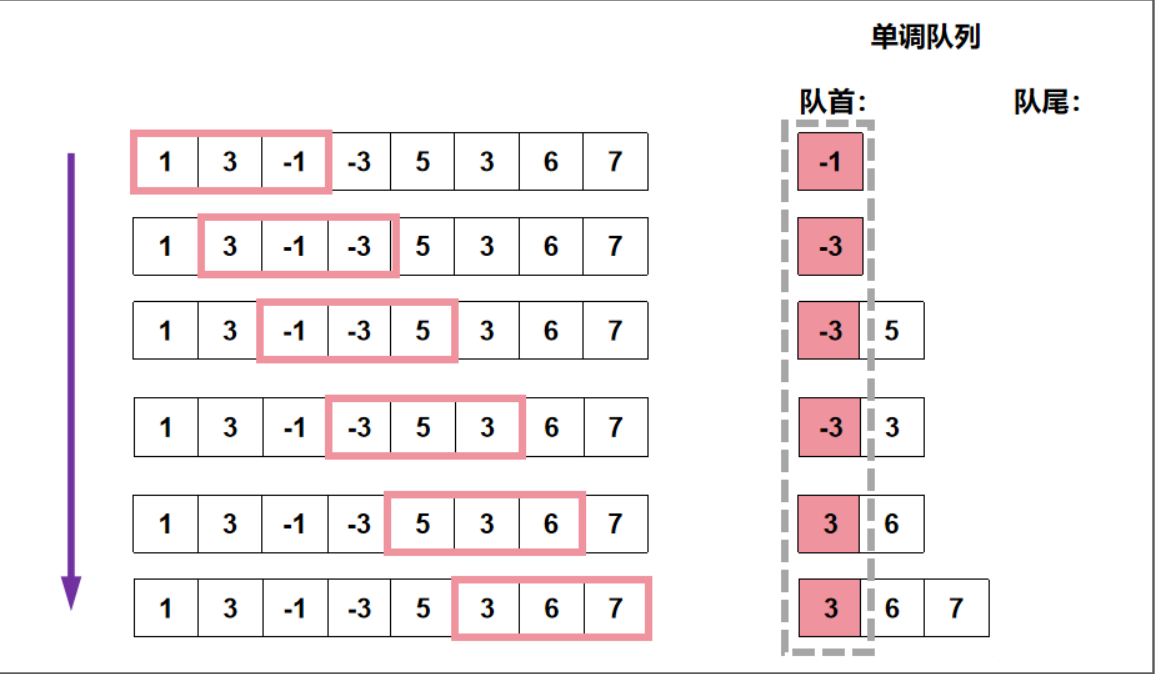
以求最大值的单调队列为例,其进出队规则如下:
该单调队列要求其中元素是从头到尾递减。遍历一个数组,所有元素依次入队。
在入队时,若该元素比队尾元素小,直接从队尾入队仍能保持单调性,那么从尾部直接入队即可。
若该元素比队尾元素大,那么要将队尾元素不停pop,直到队尾元素比该元素大(满足单调性),将该元素从队尾入队。
另外注意,当元素过期(已经不在滑动窗口内),将该元素在队首出队。
什么时候生成记录:每当形成一个窗口时就收集答案。
如何获取滑动窗口的最大值:即双端队列头部的值
理解单调队列的进出原因:
队列中的元素表示,如果此时从左往右,那么从队首到队尾的元素表示能够成为滑动窗口最大值的优先级(即哪些元素会依次称为最大值)。优先级高的元素应当值更大、值相同的情况下下标更晚过期(这就处理了具有重复值的情况)。
我们按照这样的理解来审视上面的进出队规则:
如果我们希望从队尾入队的元素比队尾已有的元素大,说明其称为最大值的优先级更高,所以需要pop掉已有的队尾元素。如果希望入队的元素比队尾已有元素小,说明其优先级低,所以可以直接入队。
对于重复值情况的说明:当即将入队的元素和队尾此时的元素重复的时候,新来的元素其下标更晚过期,所以其优先级更高,所以队中的旧元素应当被pop掉。因此队中的元素其实是严格递减的。
如何解决滑动窗口内的最小值问题呢?其实是一样的,不过我们把最小值放在队首,队中元素依次递增。
Java实现单调队列
在Java中,我们可以通过继承LinkedList类来实现一个单调队列。下面是一个简单的单调递增队列的实现示例:
import java.util.LinkedList;
public class MonotonicQueue {
private LinkedList<Integer> queue;
public MonotonicQueue() {
queue = new LinkedList<>();
}
public void offer(int num) {
// 维护单调性,移除所有比当前元素大的元素
while (!queue.isEmpty() && queue.getLast() < num) {
queue.pollLast();
}
queue.offer(num);
}
public int peek() {
return queue.peekFirst();
}
public int poll() {
return queue.poll();
}
// 检查队列是否为空
public boolean isEmpty() {
return queue.isEmpty();
}
}
单调队列的c语言(数组版)
int deque[1000];
int h = 0, t = 0;
int pop {
if (h < t) {
t--;
}
return deque[t];
}
int isEmpty() {
return h == t;
}
void push(int x) {
deque[t++] = x;
}
int peek(){
return deque[t-1];
}
int poll(){
return deque[h++];
}
int main(){
//操作,如
while(h<t&&deque[t-1]<nums[i]){
t--;
}
}
示例:
239. 滑动窗口最大值 - 力扣(LeetCode)

在队列中,索引对应的元素值是递减的,队首元素对应的元素值最大,队尾元素对应的元素值最小。
在这里双端队列来实现单调。队列中存储的是数组中元素的索引。
初始化一个h,t变量用来表示队头队尾
先从数组的第一个元素开始遍历,维护一个递减的双端队列。在这个阶段,由于窗口大小为 k,所以只需要遍历数组的前 k-1 个元素。
如果当前元素大于队尾元素,则将队尾元素出队,直到队列为空或者当前元素小于等于队尾元素。然后将当前元素的索引入队。
在这个时候,虽然队列里的东西不一定是k-1,但是初始化的窗口已经到了k-1.
然后从第 k 个元素开始遍历数组,每次遍历都会对双端队列进行维护,并且将当前窗口的最大值,也就是队头元素(h)记录在结果数组中。
在滑动窗口阶段,从第 k 个元素开始遍历数组。继续维护递减的双端队列,将当前元素入队。然后将当前窗口的最大值记录在结果数组中。
在每次左边窗口加1时,判断队首元素是否已经不在当前窗口内,如果不在,则将队首元素出队。
最后返回答案数组即可
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
int[] deque = new int[nums.length];
int h = 0, t = 0;
for (int i = 0; i < k - 1; i++) {
while (h < t && nums[deque[t - 1]] <= nums[i]) {
t--;
}
deque[t++] = i;
}
int x = nums.length - k + 1;
int[] ans = new int[x];
for (int l = 0, r = k - 1; l < nums.length - k + 1; l++, r++) {
while (h < t && nums[deque[t - 1]] <= nums[r]) {
t--;
}
deque[t++] = r;
ans[l] = nums[deque[h]];
if (deque[h] == l) {
h++;
}
}
return ans;
}
}
// 定义一个指向整数的指针数组,用于存储滑动窗口中元素的索引
int deque[numsSize];
// 初始化头部和尾部索引
int h = 0, t = 0;
// 填充双端队列的前 k-1 个元素
for (int i = 0; i < k - 1; i++) {
// 维护双端队列的单调性:移除所有比当前元素小的元素
while (h < t && nums[deque[t - 1]] <= nums[i]) {
t--;
}
// 将当前元素的索引加入到双端队列中
deque[t++] = i;
}
// 分配内存用于存储滑动窗口最大值的结果
int* ans = (int*)malloc(sizeof(int) * (numsSize - k + 1));
// 滑动窗口遍历整个数组
for (int l = 0, r = k - 1; l < numsSize - k + 1; l++, r++) {
// 维护双端队列的单调性:移除所有比当前元素小的元素
while (h < t && nums[deque[t - 1]] <= nums[r]) {
t--;
}
// 将当前窗口的最后一个元素的索引加入到双端队列中
deque[t++] = r;
// 当前窗口的最大值是双端队列头部元素对应的值
ans[l] = nums[deque[h]];
// 如果双端队列头部元素的索引正好是窗口左边界,则移除头部元素
if (deque[h] == l) {
h++;
}
}
// 更新返回的最大值数组的大小
*returnSize = numsSize - k + 1;
// 返回结果数组
return ans;
862. 和至少为 K 的最短子数组 - 力扣(LeetCode)

class Solution {
// 初始化ans为一个较大的数值,以便在遍历过程中找到更小的值
int ans = 100001;
public int shortestSubarray(int[] nums, int k) {
// deque数组用于存储当前考虑的子数组的索引,实现单调队列的功能
int[] deque = new int[nums.length + 1];
// 初始化双端队列的头和尾索引
int h = 0, t = 0;
// sum数组用于存储前缀和,sum[i]表示nums从0到i的元素和
long[] sum = new long[nums.length + 1];
// 初始化前缀和数组的第一个元素为0
sum[0] = 0;
// 循环遍历数组nums
for (int i = 0; i <= nums.length; i++) {
// 如果不是第一个元素,计算当前位置的前缀和
if (i != 0)
sum[i] = sum[i - 1] + nums[i - 1];
// 维护单调队列:移除所有使得sum[i] - sum[deque[h]] >= k的元素
// 因为这些元素之前的子数组和已经不可能满足和至少为k
while (h < t && sum[i] - sum[deque[h]] >= k) {
ans = Math.min(ans, i - deque[h++]); // 更新最短子数组长度
}
// 维护单调队列:移除所有使得sum[i] <= sum[deque[t - 1]]的元素
// 因为这些元素对于找到和至少为k的最短子数组没有帮助
while (h < t && sum[i] <= sum[deque[t - 1]]) {
t--; // 移除队尾元素
}
// 将当前元素的索引加入到单调队列中
deque[t++] = i;
}
// 如果ans没有被更新,则说明不存在和至少为k的子数组,返回-1
return ans > 100000 ? -1 : ans;
}
}
结语
单调队列是一种强大的数据结构,它在处理与窗口相关的算法问题时特别有用。通过维护队列的单调性,我们可以有效地减少不必要的计算,提高算法的效率。
希望这篇博客能够帮助您更好地理解单调队列以及如何在Java中实现和应用它。如果您有任何问题或想要了解更多信息,请在评论区告诉我。