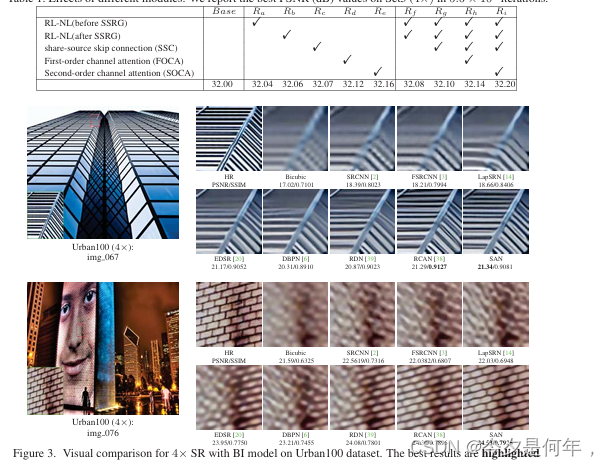
小提琴图
   小提琴图和箱线图类似，用来显示数据分布和概率密度。结合了箱线图和密度图的特征，用来显示数据的分布形状。

输入
    数据: 输入数据集 

输出
    选中的数据: 从图中选中的实例 
    数据: 增加了一列，显示数据点是否被选中 
    

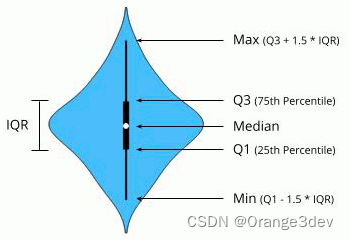
小提琴图的作用与箱形图类似。它显示了在不同类别变量的几个水平上的定量数据的分布，以便可以比较这些分布。
与箱形图不同，小提琴图中的所有组件都对应于实际数据点，而小提琴图特征的是潜在分布的高斯密度估计。

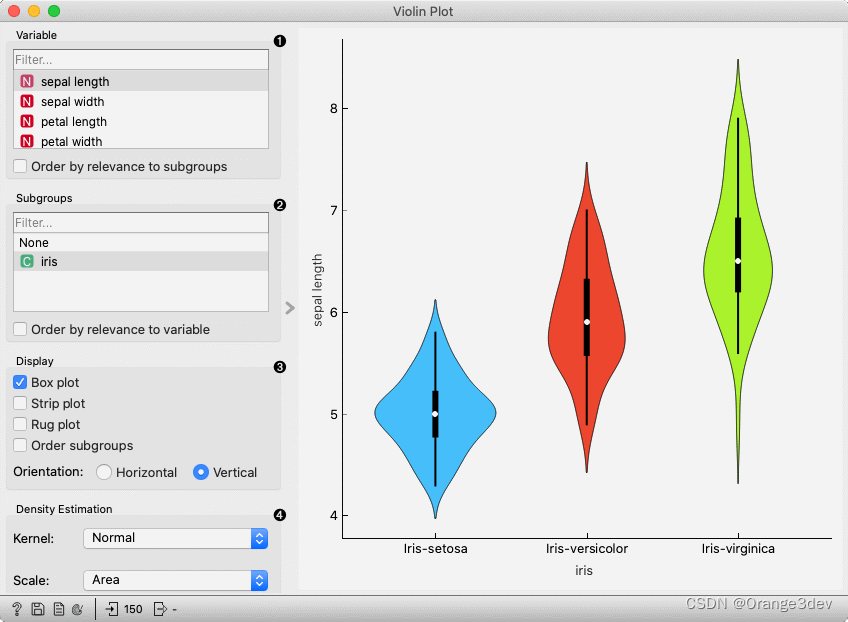
1.选择您想要绘制的变量。勾选按相关性到子组排序以按卡方或ANOVA对选定子组进行排序。
2.选择子组以显示由离散子组显示的小提琴图。勾选按相关性到变量排序以按卡方或ANOVA对选定变量进行排序。
3.箱形图: 勾选以显示底层箱形图。

带状图(Strip plot): 勾选以显示由点表示的底层数据。
  地毯图(Rug plot): 勾选以显示由线表示的底层数据。
  排序子组: 勾选以按中位数（升序）排序小提琴。
  方向: 确定小提琴的方向。
kernel density estimation 核密度估计
核函数: 选择用于估计密度的核函数。可能的核函数有：高斯、Epanechnikov 和线性。
缩放: 选择用于缩放每个小提琴宽度的方法。
      如果选择面积，每个小提琴将具有相同的面积。
      如果选择计数，小提琴的宽度将按该bin中的观察值数量进行缩放。
      如果选择宽度，每个小提琴将具有相同的宽度。

软件下载链接: https://pan.baidu.com/s/12drK7Mz7YSqrwIQk5Wh5cw?pwd=8tnd 

视频教程：关注我不迷路, 抖音：Orange3dev

https://www.douyin.com/user/MS4wLjABAAAAicBGZTE2kX2EVHJPe8Ugk3_nlJk9Nha8OZh4Bo_nTu8

1-组件概览
2-树查看器-决策树
3-箱线图-离散属性分布
4-箱线图-要素计算
5-箱线图-连续属性分布
6-小提琴图
7-分布图
8-散点图-智能数据可视化
9-散点图-探索性数据分析
10-散点图-高亮选择数据
11-折线图
12-条形图
13-筛网图
14-马赛克图
15-自由投影
16-线性投影
17-雷达图
18-热力图
19-韦恩图
20-轮廓图
21-毕达哥拉斯树
22-毕达哥拉斯森林
23-CN2规则查看器
24-诺莫图