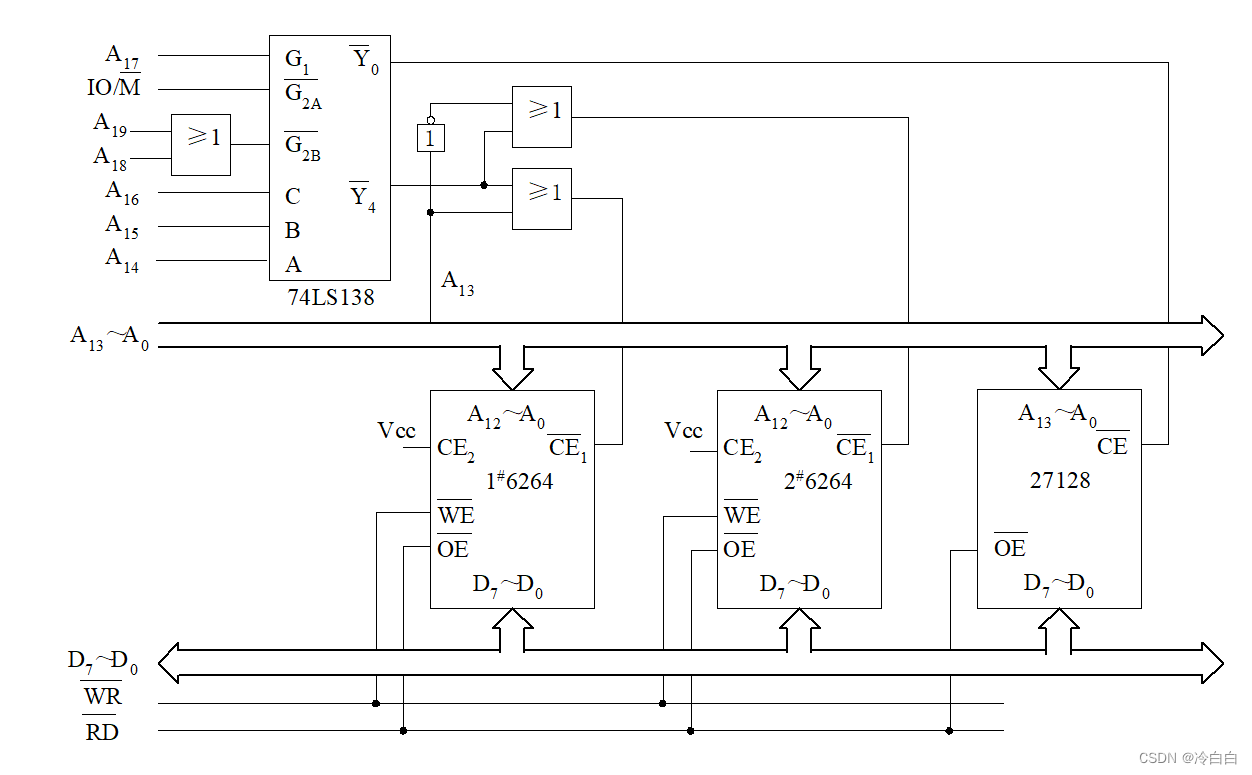
借助这一道题目来严谨证明一下Huffman树的构造方法的正确性
对任意一颗\(k\)叉huffman树,他都可以等价于一个类似于合并果子的过程,即每次取出最多\(k\)个点进行合并,然后\(k\)个点的权值和就是新的点的权值,然后把这个新的点加入决策集合,最终操作的只剩下一个点。不难证明,huffman树所求的带权路径和就是合并过程中产生的每个点的点权和(包括最开始的点)
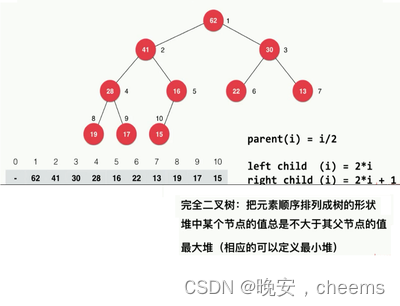
蓝书上的关于最后一次不足\(k\)个的论点给了我们一个启发:在huffman树中(没有添加权值为\(0\)的节点),除了倒数第二层(注意最后一层全部都是叶子)可能存在不满\(k\)叉的节点,从第一层到倒数第三层的所有节点的叉数都是满的;而倒数第二层也不会存在两个点或以上不满\(k\)叉,否则的话我们将这些点按顺序排好权值和显然不变,如下
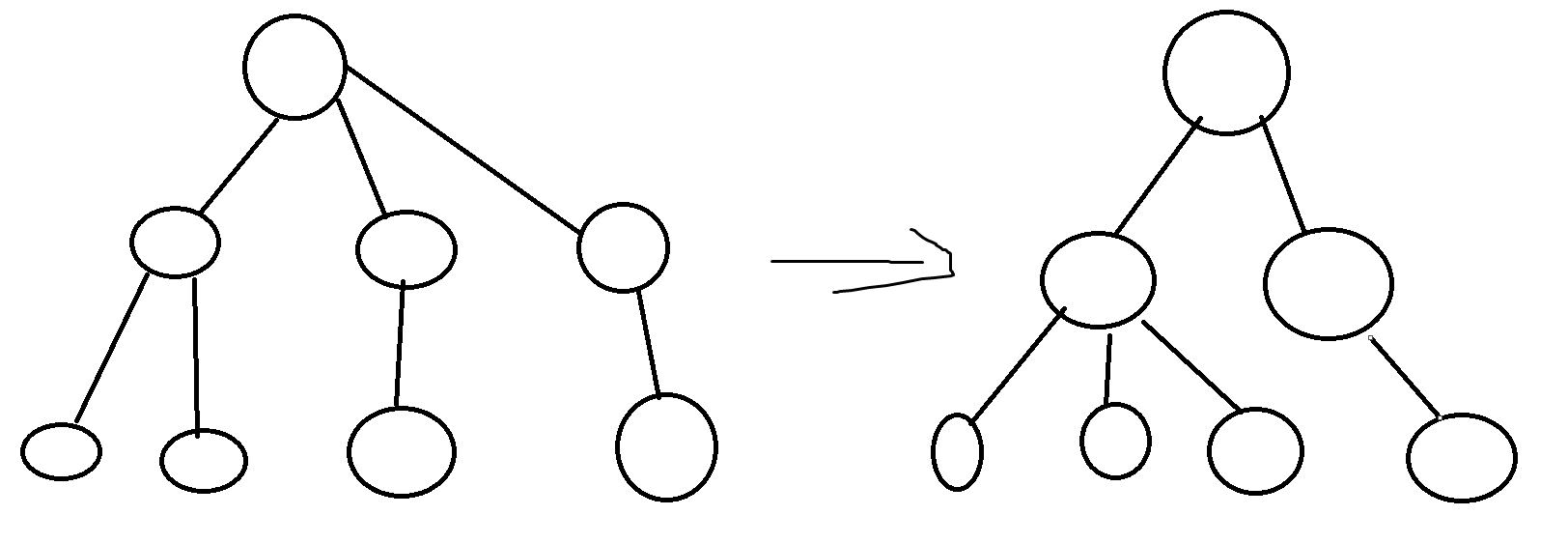
而根据我们前面的等价,上述表述就是说明我们除了可能在第一次取的时候不取满\(k\)个点,剩下的合并的时候都是一次性从决策集合里面拿\(k\)个点出来的
我们再来考察取的过程。对于任意一种合并的方案,我们显然是每次合并决策集合中最小的若干个点是最优的(用决策包容性证明,相当于越早合并被记录的次数就越多)。那么就可以构造出来一种方案了:根据我们上面的等价过程,我们只有在第一次的时候取不满\(k\)个点,剩下的时候全部都从决策集合里面拿\(k\)个点就好了。为了程序的一致性,我们在最开始的时候加入若干个零点就可以不用判断边界条件了