环境:Win10+Visual Studio 2022 Community
在本次实验中需要用到第一篇文章实验内容的代码及环境,详情请见:传送门
目录
一、实验目的
二、实验步骤
1.扫描线填充算法
2.图形的缩放算法
3.对称变换算法
4.消隐算法
5.金刚石图形算法
一、实验目的
1.熟练掌握图形的扫描线填充算法
2.熟练掌握图形缩放算法
3.熟练掌握图形的对称变换算法
4.熟练掌握图形的消隐算法
5.熟练掌握生成金刚石图案算法
二、实验步骤
1.扫描线填充算法
(1)打开工程项目,在菜单项“图形填充”下建立子菜单项“扫描线填充算法”,在其属性窗口将属性项Name的属性值改为“ScanLineFill”。

(2)双击菜单项“扫描线填充算法”,系统建立一个空的菜单响应函数ScanLineFill_Click。在该函数中加入如下语句:
private void ScanLineFill_Click(object sender, EventArgs e)
{
MenuID = 31;
PressNum = 0;
Graphics g = CreateGraphics(); //创建图形设备
g.Clear(BackColor1); //设置背景颜色
}(3)在窗口类Form1中增加一个数组group用来存放图形顶点。因为其他的算法也需要这样的数组,因此将其增设在Form1类成员中。
Point[] group = new Point[100]; //创建一个能放100个点的点数组(4)在Form1_MouseClick函数中,增加菜单指示变量MenuID为31(即开始扫描线填充算法)时的程序操作语句如下:
if (MenuID == 31) //扫描线填充算法
{
if (e.Button == MouseButtons.Left) //如果按左键,存顶点
{
group[PressNum].X = e.X;
group[PressNum].Y = e.Y;
if (PressNum > 0) //依次画多边形
{
g.DrawLine(Pens.Red, group[PressNum - 1], group[PressNum]);
}
PressNum++; //记录多边形顶点数
}
if (e.Button == MouseButtons.Right) //如果按右键,结束顶点采集,开始填充
{
g.DrawLine(Pens.Red, group[PressNum - 1], group[0]); //最后一条边
ScanLineFill1(); //调用填充算法,开始填充
PressNum = 0; //清零,为绘制下一个图形做准备
}
}(5)在Form1_MouseMove函数中,增加菜单指示变量MenuID为31时的程序操作语句如下:
if (MenuID == 31 && PressNum > 0)
{
if (!(e.X == OldX && e.Y == OldY))
{
g.DrawLine(BackPen, group[PressNum - 1].X, group[PressNum - 1].Y, OldX, OldY);
g.DrawLine(MyPen, group[PressNum - 1].X, group[PressNum - 1].Y, e.X, e.Y);
OldX = e.X;
OldY = e.Y;
}
}(6)ScanLineFill1函数是用来实现算法的函数,到现在为止还没实现。系统不能容忍一个还没实现的函数被使用,因此会提示错误。为消除错误,建立一个空函数如下:
private void ScanLineFill1()
{
}(7)按F5键编译执行,可以用鼠标点击一系列左键,确定封闭多边形顶点位置,点击鼠标右键,结束多边形顶点选择,多边形自动封闭,在窗口中画出封闭多边形。
(8)现在实现扫描线算法。首先,应该建立边结构,边结构中保留了每一条非水平边的信息。一条边基本信息是两个端点,为了后续算法顺利进行,将信息组织为上端的Y坐标、下端点的X坐标和斜率的倒数。在教科书中,以下端点的Y坐标对边结构进行分类,每条边下端点的Y坐标信息暗含在ET表中,为了编程方便,本书将下端点的Y坐标也建立在边结构中。因此,在Form1类中建立如下结构数据类型:
public struct EdgeInfo
{
int ymax, ymin; //Y的上下端点
float k, xmin; //斜率倒数和X的下端点
//为四个内部变量设置的公共变量,方便外界存放数据
public int YMax
{
get { return ymax; }
set { ymax = value; }
}
public int YMin
{
get { return ymin; }
set { ymin = value; }
}
public float XMin
{
get { return xmin; }
set { xmin = value; }
}
public float K
{
get { return k; }
set { k = value; }
}
//构造函数,这里用来初始化结构变量
public EdgeInfo(int x1, int y1, int x2, int y2) //(x1,y1):下端点;(x2,y2):上端点
{
ymax = y2;
ymin = y1;
xmin = (float)x1;
k = (float)(x1 - x2) / (float)(y1 - y2);
}
}(9)group数组中依次存放着封闭多边形顶点,相邻的两个点构成封闭多边的一条边。首先需要根据group数组中的各条边,建立各边的边结构。设立一个边结构数组edgelist,从group数组中依次取出每一条边,生成边结构,存入边结构数组;
(10)按照算法,还要建立ET表和AEL表,并随着扫描线的不断上移,将ET表中的边逐步插入AEL表,并按算法改变边结构中的数据。如果严格按照算法执行,编程难度很大。分析算法可知,具体的填充是在AEL表中完成,而AEL表由ET表中与扫描线相交的边(即ymin>=y<ymax)组成,只要根据当前扫描线位置y从边结构数组中找出所有与扫描线相交的边结构,就得到当前AEL表,就可以进行扫描线填充。这样就不需要建立结构复杂、难以表达的ET表了,因此编程实现方法可以直接建立AEL表。必须解决的一个问题是算法的结束条件。按照算法,当ET表和AEL表均为空时,算法结束,现在没有ET表了,如何结束?分析算法整个过程,对于一个图形的填充,扫描线的有效范围是从图形的最低点到图形的最高点。因此,对于存在与Group数组中的图形,只要找到了图形的最低点和最高点,扫描线运动范围就确定了。为此,要设置两个变量,确定算法操作范围,插入如下语句:
private void ScanLineFill1()
{
EdgeInfo[] edgelist = new EdgeInfo[100]; //建立边结构数组
int j = 0, yu = 0, yd = 1024; //活化边的扫描范围从yd到yu
group[PressNum] = group[0]; //将第一点复制为数组最后一点
for (int i = 0; i < PressNum; i++) //建立每一条边的边结构
{
if (group[i].Y > yu)
{
yu = group[i].Y; //找出图形最高点
}
if (group[i].Y < yd)
{
yd = group[i].Y; //找出图形最低点
}
if (group[i].Y != group[i + 1].Y) //只处理非水平边
{
if (group[i].Y > group[i + 1].Y) //下端点在前,上端点在后
{
edgelist[j++] = new EdgeInfo(group[i + 1].X, group[i + 1].Y, group[i].X, group[i].Y);
}
else
{
edgelist[j++] = new EdgeInfo(group[i].X, group[i].Y, group[i + 1].X, group[i + 1].Y);
}
}
}
Graphics g = CreateGraphics();
for (int y = yd; y < yu; y++)
{
var sorted = from item in edgelist //定义存放选择结果的集合,从edgelist中选边结构
where y < item.YMax && y >= item.YMin //选择条件
orderby item.XMin, item.K //集合元素排序条件
select item; //开始选
int flag = 0; //设置一个变量用来标记是第一个还是第二个点
foreach (var item in sorted) //两两配对,画线
{
if (flag == 0) //第一点
{
FirstX = (int)(item.XMin + 0.5); //取点,改标记,不画
flag++;
}
else //第二点
{
g.DrawLine(Pens.Blue, (int)(item.XMin + 0.5), y, FirstX - 1, y); //画,改标记
flag = 0;
}
}
for (int i = 0; i < j; i++) //将dx加到x上
{
if (y < edgelist[i].YMax - 1 && y > edgelist[i].YMin) //选出与当前扫描线相交的边
{
edgelist[i].XMin += edgelist[i].K; //修改边结构中X域的数值
}
}
}
}(11)运行结果

2.图形的缩放算法
(1)先建立对话框。如图所示,右击项目名,在弹出的菜单中鼠标指向“添加(D)”-“新建项(W)”。

系统弹出添加窗口如图所示。在窗口中,依次选择“C#项”-“窗体(Windows窗体)”。

此时,“名称”栏目中有“Form2.CS”,它是新建窗口的后台程序文件,该文件名可以修改,我们这里不做修改。点击“添加”按键,一个新的窗体出现,同时Form2.CS出现在解决方案栏目中。系统实际上建立了一个类来管理该窗口。
(2)点击解决方案栏目中Form2.CS,打开“Form2.cs设计”页面,新建窗体出现。选择该窗体,在右下角窗体属性栏中,将Name属性值改为“MyForm",将Text属性值设置为“请输入缩放系效”。
 | 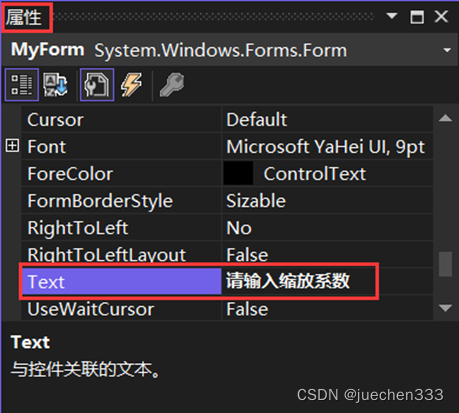 |
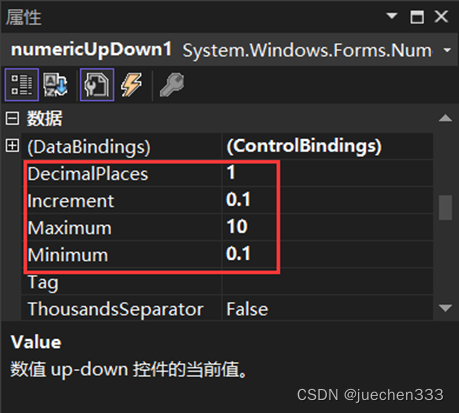
(3)从工具箱的公共控件类中向该窗体中拖入添加两个“Lable”控件,两个“NumericUpDown”控件,两个“Button”控件。两个“Lable”控件的Text属性值分别设置为“X方向缩放系数:”、“Y方向缩放系数:”。将两个“NumericUpDown”控件的属性值均做如下修改。DecimalPlaces:1,Increment:0.1,Maximum:10,Minimum:0.1,Value:1。将两个Button控件Text属性值设置为“确认”和“取消”,确认按键的“DialogResult”属性值设置为“OK”,将取消按键的“DialogResult”属性值设置为“Cancel"。
 |  |
 |  |
 |  |
调整各控件的位置,结果如图:

(4)分别双击窗体中的“确认”、“取消”按键,系统在Form2.cs文件中自动建立两个按键响应空函数 button1_Click 和 button2_Click。在“确认”按键的响应函数中添加如下内容,“取消”按键响应函数不添加:
private void button1_Click(object sender, EventArgs e)
{
xscale = (float)numericUpDown1.Value;
yscale = (float)numericUpDown2.Value;
}
private void button2_Click(object sender, EventArgs e)
{
}(5)xscale和 yscale是类内的两个内部变量,用来接收窗口输入系数,但目前还没定义。在类中加入如下语句定义它们,类中的私有变量要能为外部所用必须设置对应的公有变量,并对公有变量做如下安排:
private float xscale, yscale;
public float Xscale
{
get { return this.xscale; }
}
public float Yscale
{
get { return this.yscale; }
}(6)缩放系数必须设置初值,以避免其为0.他们的设置可以安排在类的构造函数中完成。
public MyForm()
{
xscale = (float)1.0;
yscale = (float)1.0;
InitializeComponent();
}(7)回到Form1.cs[设计]页面上,在菜单项“二维图形变换”下建立子菜单项“图形缩放”,将其属性项Name的属性值改为英文字符“TransScale”。

(8)双击菜单项建立菜单响应数TransScale_Click。由于本变换不需要鼠标操作,因此只需要加入菜单选择标示和必要的变量,在系统建立的空响应函数中加人语句如下:
private void TransSacle_Click(object sender, EventArgs e)
{
MenuID = 13;
float xs, ys;
MyForm myf = new MyForm(); //创建对话框对象
if (myf.ShowDialog() == DialogResult.Cancel) //打开建立的对话框,接受变换系数
{
myf.Close(); //如果选择的是“取消”,则关闭对话框,退出
return;
}
xs = myf.Xscale;
ys = myf.Yscale;
myf.Close();
Graphics g = CreateGraphics(); //创建图形设备
pointsgroup[0] = new Point(100, 100); //画原图形
pointsgroup[1] = new Point(200, 100);
pointsgroup[2] = new Point(200, 200);
pointsgroup[3] = new Point(100, 200);
g.DrawPolygon(Pens.Red, pointsgroup); //原图形存在与图形设备g中
Matrix myMatrix = new Matrix(); //建立矩阵变量,为计算复合矩阵做准备
myMatrix.Translate(-100, -100); //根据缩放中心,建立平移矩阵
myMatrix.Scale(xs, ys, MatrixOrder.Append); //右乘缩放矩阵
myMatrix.Translate(100, 100, MatrixOrder.Append); //右乘平移矩阵
g.Transform = myMatrix; //用得到的符合矩阵对图形进行变换
g.DrawPolygon(Pens.Blue, pointsgroup); //画变换后的图形
}(9)运行结果

3.对称变换算法
(1)在菜单项“二维图形变换”下建文子菜单项“对称变换”,将其属性项Name的属性值改为英文字符“TransSymmetry”。

(2)双击菜单项建立菜单响应函数TransSymmetry_Click,在该函数中加入语句如下:
private void TransSymmetry_Click(object sender, EventArgs e)
{
MenuID = 14;
PressNum = 0;
Graphics g = CreateGraphics(); //创建图形设备
pointsgroup[0] = new Point(100, 100);
pointsgroup[1] = new Point(200, 100);
pointsgroup[2] = new Point(200, 200);
pointsgroup[3] = new Point(100, 200);
g.DrawPolygon(Pens.Red, pointsgroup);
}(3)在Form1_MouseClick函数中加入语句如下:
if (MenuID == 14) //对称变换
{
if (PressNum == 0) //保留第一点
{
FirstX = e.X;
FirstY = e.Y;
}
else //第二点
{
g.DrawLine(Pens.CadetBlue, FirstX, FirstY, e.X, e.Y); //画对称变换基线
TransSymmetry1(FirstX, FirstY, e.X, e.Y);
}
PressNum++;
if (PressNum > 2)
{
PressNum = 0; //完毕,清零,为下一次做准备
(4)我们知道,这里涉及的二维矩阵都是仿射变换矩阵,最后一列都是![]() ,因此,创建矩阵只需要给出前面6个有效参数,在TransSymmetry_Click函数后面添加TransSymemetry1函数实现语句,如下所示:
,因此,创建矩阵只需要给出前面6个有效参数,在TransSymmetry_Click函数后面添加TransSymemetry1函数实现语句,如下所示:
private void TransSymmetry1(int x1, int y1, int x2, int y2)
{
if (x1 == x2 && y1 == y2) { return; } //排除两点重合的情况
double angle;
if (x1 == x2 && y1 < y2) //特殊角
{
angle = 3.1415926 / 2.0;
}
else if (x1 == x2 && y1 > y2) //特殊角
{
angle = 3.1415926 / 2.0 * 3.0;
}
else
{
angle = Math.Atan((double)(y2 - y1) / (double)(x2 - x1));
}
angle = angle * 180.0 / 3.1415926; //将弧度转化为角度
Matrix myMatrix = new Matrix(); //建立矩阵变量,为复合矩阵计算做准备
myMatrix.Translate(-x1, -y1); //根据缩放中心,建立平移矩阵
myMatrix.Rotate(-(float)angle, MatrixOrder.Append); //右乘旋转矩阵
Matrix MyM1 = new Matrix(1, 0, 0, -1, 0, 0); //创建对称变换矩阵
myMatrix.Multiply(MyM1, MatrixOrder.Append); //右乘对称变换矩阵
myMatrix.Rotate((float)angle, MatrixOrder.Append); //右乘变换矩阵
myMatrix.Translate(x1, y1, MatrixOrder.Append); //右乘平移矩阵
Graphics g = CreateGraphics(); //创建图形设备
g.Transform = myMatrix; //用得到的复合矩阵对图形进行变换
g.DrawPolygon(Pens.Blue, pointsgroup); //变换后的图形
}(5)运行结果

4.消隐算法
(1)打开工程项目,选择菜单项“消隐”,添加“地形显示1”子项,将其属性项Name的属性值改为英文字符“Terrain1”。

(2)双击菜单项建立菜单响应函数Terrain1_Click,在系统建立的空的响应函数中加入语句如下:
private void Terrain1_Click(object sender, EventArgs e)
{
MenuID = 51;
Terrain11();
}(3)为了简化编程,DEM数据规定为一个200×200的 ASCII码数据文件,文件名为DEM.dat,存放于桌面文件夹1下。
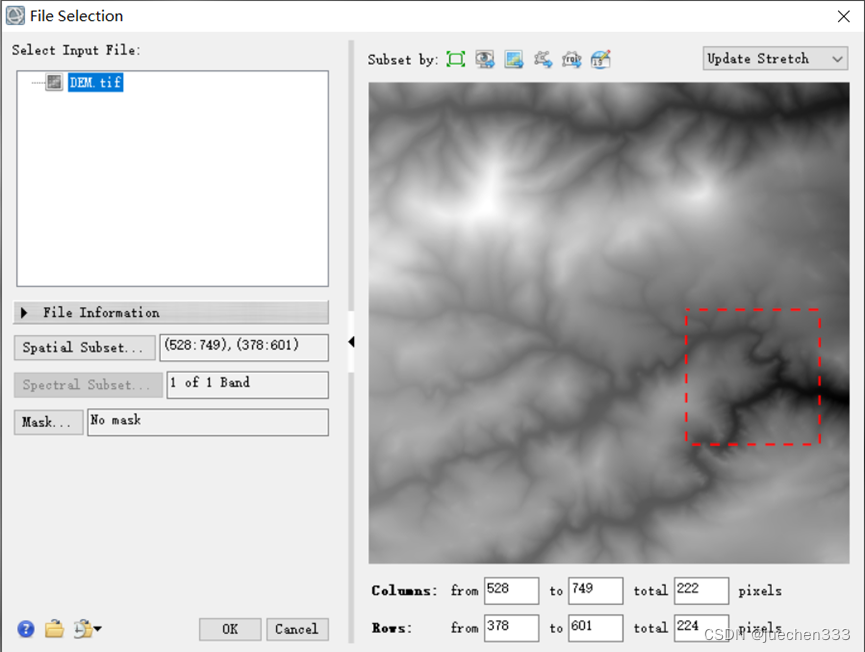
数据来源于(ENVI遥感图像处理方法(第二版) 第十一章 随书光盘数据),由于数据偏大,在ENVI中进行裁剪,如图所示,得到DEM.dat数据。

(4)建立函数Terrain11,如下所示:
private void Terrain11()
{
int[,] DEM = new int[200, 200]; //建立数组存放DEM数据
DEM = ReadDEM(); //读入高程数据
int size = 3; //柱状体的底面积设置为size*size
double ky = 0.4, kz = 0.3; //深度值对投影位置的影响比例系数
Graphics g = CreateGraphics(); //创建图形设备
g.Clear(Color.LightGray); //清空绘图区
int dy = (int)(ky * size + 0.5); //深度值对投影位置的影响值
int dz = (int)(kz * size + 0.5);
for (int i = 0; i < 200; i++)
{
for (int j = 0; j < 200; j++)
{
int y = (int)(j * size - i * size * ky); //Ky=0.4,Kz=0.3
int z = (int)(-i * size * kz); //柱状体基点为空间点(i,j,0)的投影点
DrawPixel(g, dy, dz, size, y, z, DEM[i, j]); //画高程值DEM[i,j]对应的柱状体
}
}
}(5)函数ReadDEM将硬盘中的DEM数据文件读入,其实现方法如下:
private int[,] ReadDEM()
{
int[,] D = new int[200, 200]; //建立数组存放DEM
FileStream fs = new FileStream("C:\\Users\\juechen\\Desktop\\1\\DEM.dat", FileMode.Open, FileAccess.Read);
BinaryReader r = new BinaryReader(fs);
for (int i = 0; i < 200; i++)
{
for (int j = 0; j < 200; j++)
{
D[i, j] = r.ReadByte();
}
}
return D;
}(6)该函数根据文件数据以二进制格式存取且大小为200×200等已知信息,直接运用流方式实现,是一种简化的方法。大多数的实际数据文件都有一个文件首部描述文件的组织信息,一般需要先读出首部信息,然后根据首部信息生成数据存放结构变量,确定读数据方法。该函数运用的流方式中的数据类型、方法等属于系统提供的System.IO命名空间,因此需要事先说明命名空间,方法是在程序的顶端加入以下语句:
using System.IO;(7)函数DrawPixel绘制高程值DEM[i , j]对应的柱状体。由于程序所使用的System. Drawing.Drawing2D命名空间没有提供直接绘制三维柱状体的方法,该函数用绘制3个填充四边形的方法来实现,方法如下:
private void DrawPixel(Graphics g, int dx, int dy, int size, int x, int y, int z)
{
x += 200; //X,Y方向适当偏移,以调整场景显示位置
y = -y + 300; //Y方向需要颠倒
Point[] pts = new Point[4];
pts[0].X = x - dx;
pts[0].Y = y + dy; //y方向增量也需要颠倒,即y-dy变成y+dy
pts[1].X = x - dx;
pts[1].Y = y + dy - z;
pts[2].X = x - dx + size;
pts[2].Y = y + dy - z;
pts[3].X = x - dx + size;
pts[3].Y = y + dy;
g.FillPolygon(Brushes.White, pts);
g.DrawPolygon(Pens.Black, pts);
pts[0].X = x;
pts[0].Y = y - z;
pts[1].X = x - dx;
pts[1].Y = y + dy - z;
pts[2].X = x - dx + size;
pts[2].Y = y + dy - z;
pts[3].X = x + size;
pts[3].Y = y - z;
g.FillPolygon(Brushes.White, pts);
g.DrawPolygon(Pens.Black, pts);
pts[0].X = x + size;
pts[0].Y = y;
pts[1].X = x;
pts[1].Y = y - z;
pts[2].X = x - dx + size;
pts[2].Y = y + dy - z;
pts[3].X = x - dx + size;
pts[3].Y = y + dy;
g.FillPolygon(Brushes.White, pts);
g.DrawPolygon(Pens.Black, pts);
}(8)运行结果

5.金刚石图形算法
(1)先建立对话框。如图所示,右击项目名,在弹出的菜单中鼠标指向“添加(D)”-“新建项(W)”。

系统弹出添加窗口如图所示。在窗口中,依次选择“C#项”-“窗体(Windows窗体)”。

此时,“名称”栏目中有“Form3.CS”,它是新建窗口的后台程序文件,该文件名可以修改,我们这里不做修改。点击“添加”按键,一个新的窗体出现,同时Form3.CS 出现在解决方案栏目中。系统实际上建立了一个类来管理该窗口。
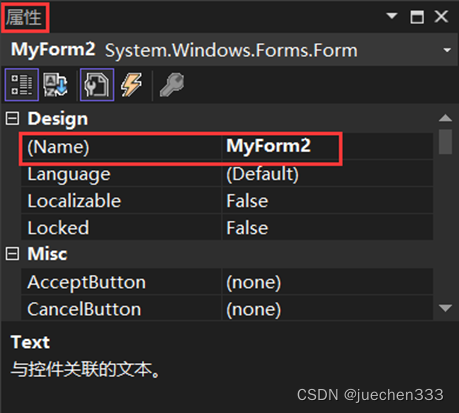
(2)点击解决方案栏目中Form3.CS,打开“Form3.cs设计”页面,新建窗体出现。选择该窗体,在右下角窗体属性栏中,将Name属性值改为“MyForm2",将Text属性值设置为“请输入参数”。
 |  |
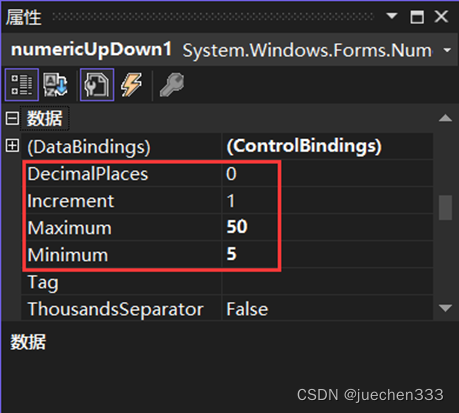
(3)从工具箱的公共控件类中向该窗体中拖入添加两个“Lable”控件,两个“NumericUpDown”控件,两个“Button”控件。两个“Lable”控件的Text属性值分别设置为“等分点个数n(5-50):”、“圆的半径r(100-400):”。将第一个“NumericUpDown”控件的属性值做如下修改。DecimalPlaces:0,Increment:1,Maximum:50,Minimum:5,Value:25,将第二个“NumericUpDown”控件的属性值做如下修改。DecimalPlaces:0,Increment:1,Maximum:400,Minimum:100,Value:200。将两个Button控件Text属性值设置为“确认”和“取消”,确认按键的“DialogResult”属性值设置为“OK”,将取消按键的“DialogResult”属性值设置为“Cancel"。
 |  |
 |  |
 |  |
调整各控件的位置,结果如图:

(4)分别双击窗体中的“确认”、“取消”按键,系统在Form2.cs文件中自动建立两个按键响应空函数 button1_Click 和 button2_Click。在“确认”按键的响应函数中添加如下内容,“取消”按键响应函数不添加:
private void button1_Click(object sender, EventArgs e)
{
n = (int)numericUpDown1.Value;
r = (int)numericUpDown2.Value;
}
private void button2_Click(object sender, EventArgs e)
{
}(5)n和r是类内的两个内部变量,用来接收窗口输入系数,但目前还没定义。在类中加入如下语句定义它们,类中的私有变量要能为外部所用必须设置对应的公有变量,并对公有变量做如下安排:
private int n, r;
public int N
{
get { return n; }
}
public int R
{
get { return r; }
}(6)缩放系数必须设置初值,以避免其为0.他们的设置可以安排在类的构造函数中完成。
public MyForm2()
{
n = 25;
r = 200;
InitializeComponent();
}(7)回到Form1.cs[设计]页面上,在菜单项“基本图形生成”下建立子菜单项“金刚石图案”,将其属性项Name的属性值改为英文字符“Diamond”。
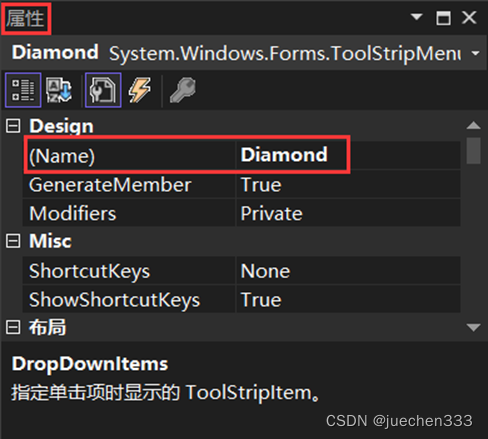
(8)双击菜单项建立菜单响应数Diamond_Click。由于本变换不需要鼠标操作,因此只需要加入菜单选择标示和必要的变量,在系统建立的空响应函数中加人语句如下:
private void Diamond_Click(object sender, EventArgs e)
{
MenuID = 55;
int n , r; //n为等分点的个数,r为圆的半径
MyForm2 myf2 = new MyForm2(); //创建对话框
if(myf2.ShowDialog() == DialogResult.Cancel) //打开建立的对话框,接受等分点个数和半径
{
myf2.Close(); //如果选择的是“取消”,关闭对话框,退出
return;
}
n = myf2.N;
r = myf2.R;
myf2.Close();
int maxX;
int maxY;
maxX = 800;
maxY = this.ClientRectangle.Bottom - SystemInformation.MenuHeight + 50;
Graphics g = CreateGraphics(); //创建图形设备
double Thta;//thta为圆的等分角
Thta = 2 * 3.1415926 / n;
for (int i = 0; i < n; i++)
{
group[i].X = (int)(r * Math.Cos(i * Thta) + maxX / 2);
group[i].Y = (int)(r * Math.Sin(i * Thta) + maxY / 2);
}
for (int i = 0; i <= n - 2; i++)
{
for (int j = i + 1; j <= n - 1; j++)
{
g.DrawLine(Pens.Blue, group[i].X, group[i].Y, group[j].X, group[j].Y);
}
}
}(9)运行结果
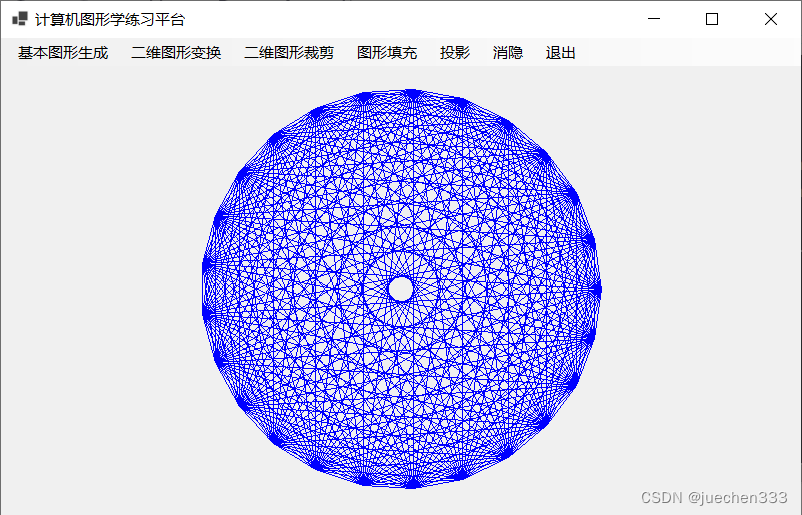





![[319]. 灯泡开关](https://img-blog.csdnimg.cn/9b03f63c842d410aad509338dd0b7394.png)