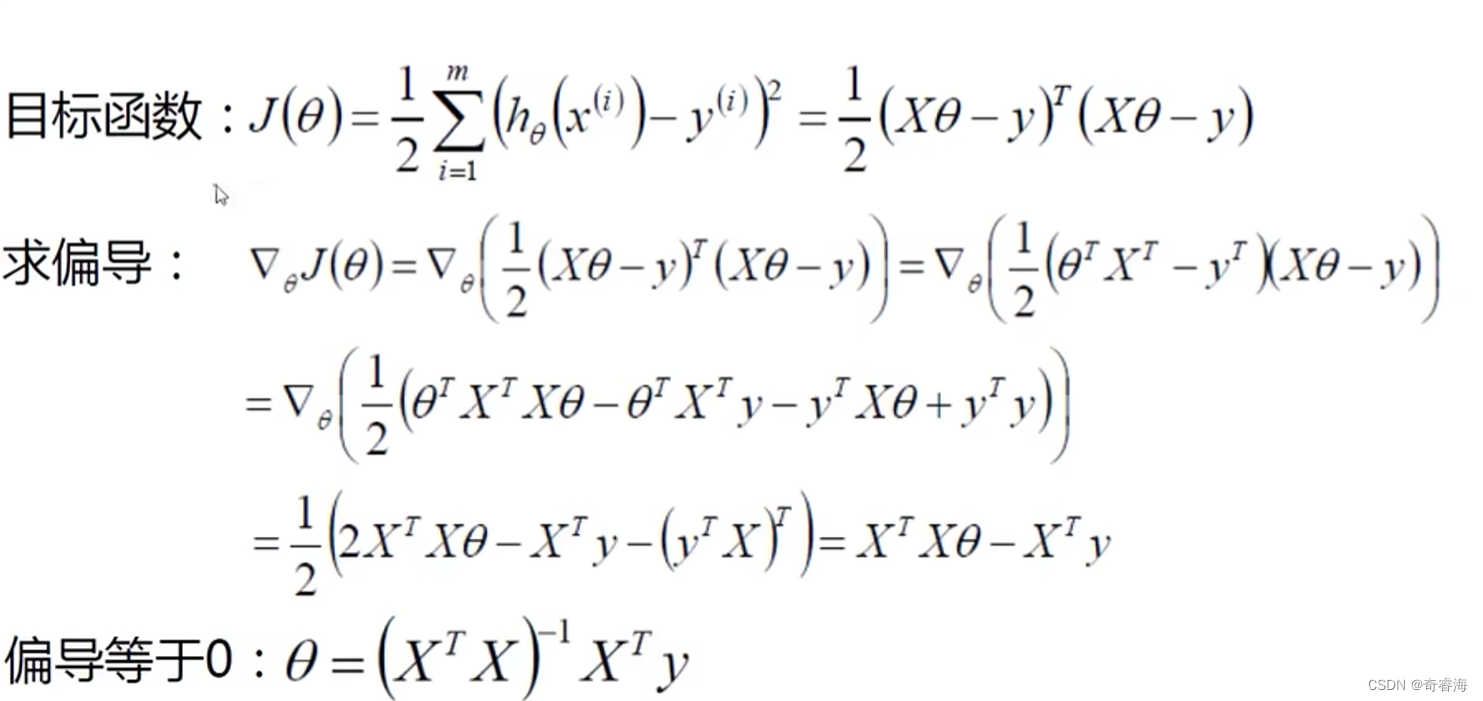线性回归是机器学习中监督学习中最基础也是最常用的一种算法。
背景:当我们拿到一堆数据。这堆数据里有参数,有标签。我们将这些数据在坐标系中标出。我们会考虑这些数据是否具有线性关系。简单来说 我们是否可以使用一条线或者一个平面去拟合这些数据的分布。
什么是线性回归
- 线性:因变量(通常是我们想要预测的变量)与自变量之间的关系可以用一个线性方程来描述。
- 回归:建立一个模型,该模型能够描述因变量与自变量之间的关系,并且可以用来预测因变量的数值
线性回归的步骤
1、列出自变量与因变量的关系式。如:
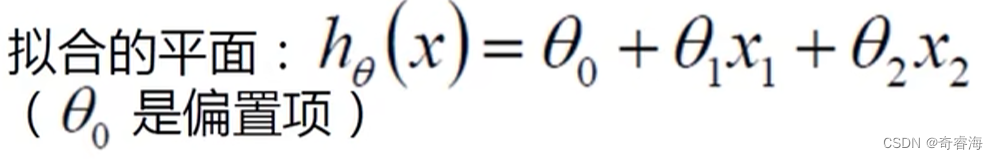
2、整合:θ0后添加一个常为1的X。上面的式子变为下面的式子
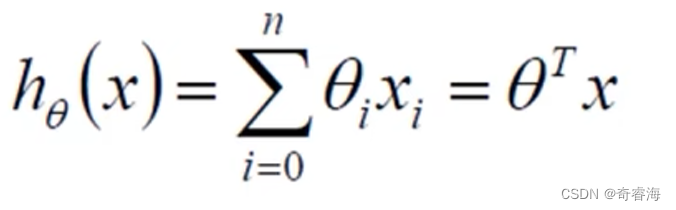
上式中,x是我们知道的,θ是各个权重,是我们要求解的。
3、目标:将真实值与预测值的差值变为最小
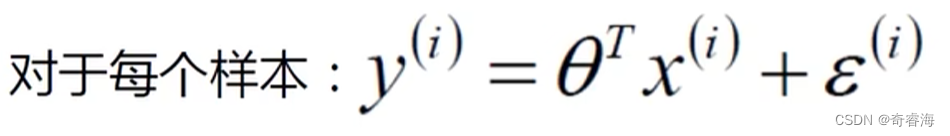
上式中,y是我们的真实值,θx是我们的预测值,ϵ是误差
4、关于误差的说明

我们根据上面误差的说明可以得到:
1、
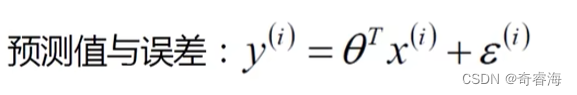
2、
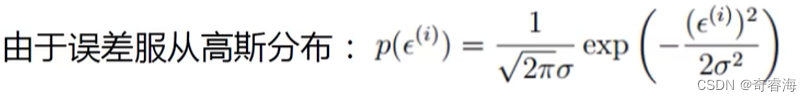
3、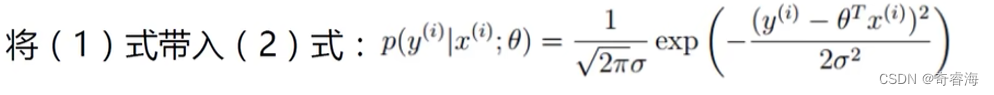
这里我们要先明确,我们的目的是算出θT 这个权重矩阵。且 独立同分布的联合概率密度函数等于各个维度的边缘概率密度函数的乘积
我们可以得到似然函数

我们看上面这个似然函数。当m很大时,我们要求解就不太实际了。又因为我们是想得到我们的预测值跟真实值最接近的参数。所以我们可以尝试将乘法转化为加法。
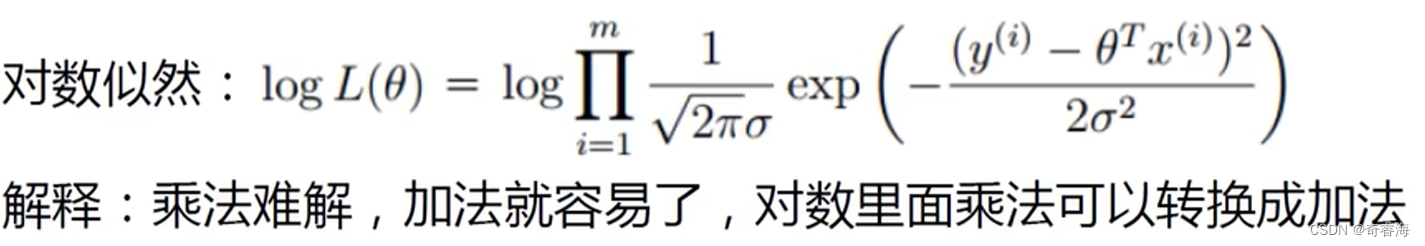
上面式子可以将累乘展开简化成累加
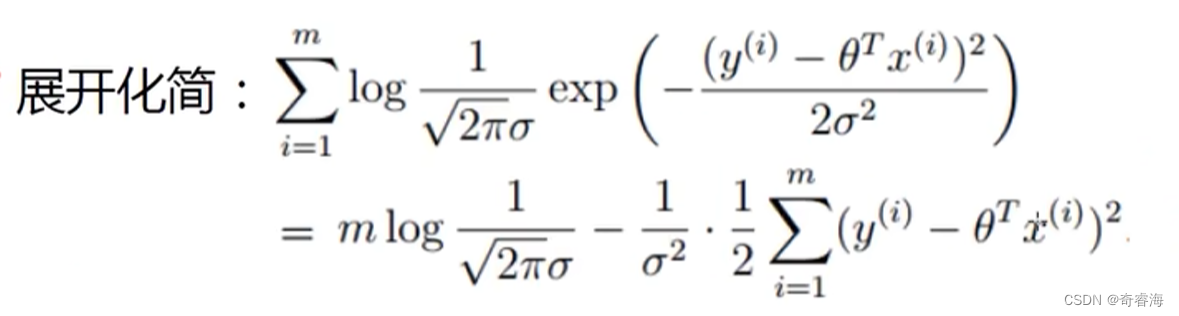
又因为上面式子中,只有y和θ是变化的,其他参数都可以看作是常量。且我们要得到这个式子的最大值。

想要这个式子的值最大。求 A - B 的最大值,且A是常量,也就是求B的最小值。
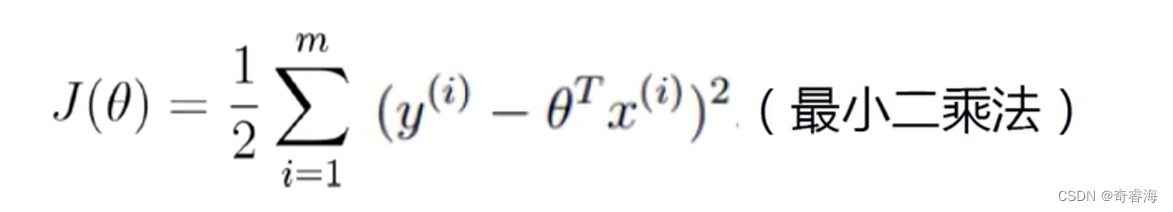
求解: