送给大家一句话：
生活坏到一定程度就会好起来，因为它无法更坏。努力过后，才知道许多事情，坚持坚持，就过来了。 – 宫崎骏 《龙猫》

┌(˘⌣˘)ʃ┌(˘⌣˘)ʃ┌(˘⌣˘)ʃ
┌(˘⌣˘)ʃ┌(˘⌣˘)ʃ┌(˘⌣˘)ʃ
┌(˘⌣˘)ʃ┌(˘⌣˘)ʃ┌(˘⌣˘)ʃ

---

1 前言

今天我们继续加强对前缀和算法。
前缀和算法是对数组进行预处理操作，进而避免大量重复的操作！使得算法性能增强！
适用于对数组有大量重复操作的问题，一维预处理较简单，二维比较复杂，画图分析可以顺利解决！

2 Leetcode 560. 和为 K 的子数组

上链接：560. 和为 K 的子数组

题目描述

题目是好理解的，我们要在nums数组中找到满足和为K的子数组。注意这里的子数组是连续的！！！不是数学上的子数组哦！！！
来看样例：

• 输入：nums = [1,1,1], k = 2
• 输出：2

很明显满足条件的是[1 ，1] 和[1 ， 1]。

算法思路

首先最好想的就是暴力枚举算法O(n^2)：

1. 从 0 开始依次枚举子数组的和
2. 满足条件计数+1

这样毋庸置疑是会超时的。并且会有大量的重复操作，求了许多重复的和。那么是不是就可以进行前缀和优化呢：
我们加入预处理：

int subarraySum(vector<int>& nums, int k) {
        //sort(nums.begin() , nums.end());
        int sum[20001] = {0};
        sum[0] = 0; 
        //0 1 2 3
        for(int i = 1 ; i <= nums.size() ; i++)
            sum[i] = sum[i - 1] + nums[i - 1];
        
        int count =  0;
        // 
        for(int i = 0 ; i <= nums.size() ; i++)
        {
            for(int j = 0 ; j < i ; j++)
            {
                if(sum[i] - sum[j] == k) count++;
            }
        }
        return count;
    }

定睛一看，这这这好像时间复杂度还不如暴力算法啊，这个的时间复杂度是O(n^2) + O( n )，也会超时。那这应该怎么处理呢？？？

双指针（滑动窗口）可以吗？不可以，因为题目并没有说是有序数组，那么就不能保证左右指针移动方向一致！！！

我们引入一个概念：以下标为 i 结尾的子数组 。我们来分析一下

1. 假如我们枚举到 第 i 个数字，得到了当前的前缀和 sum，
2. 那么如果想要得到满足和为 k 的子数组，就要寻找前缀和为 sum - k的数组
3. 那么前缀和为sum - k的数组怎么得到呢？？？使用哈希算法
4. 每次的枚举都要对当前的前缀和对应的个数进行 +1
5. 这样以后调用就方便了

    int subarraySum(vector<int>& nums, int k) {
        
        //哈希优化
        unordered_map<int , int> hash1;// 前缀和 -> 个数
        //特视情况处理
        hash1[0] = 1;
        int sum = 0; int count = 0;
        for(int i = 0; i < nums.size() ; i++)
        {
        	//记录当前前缀和
            sum += nums[i];
            //计数加上[sum - k]对应的个数
            count += hash1[sum - k];
            //把当前的前缀和统计上
            hash1[sum]++;
        }

        return count;
    }

提交看看：过啦！！！

3 Leetcode 974. 和可被 K 整除的子数组

上链接：974. 和可被 K 整除的子数组

题目描述

这个题目要求我们寻找 和 可以被 k 整除的子数组，很好理解。来看样例：

• 输入：nums = [4,5,0,-2,-3,1], k = 5
• 输出：7
• 解释：有 7 个子数组满足其元素之和可被 k = 5 整除：
  [4, 5, 0, -2, -3, 1], [5], [5, 0], [5, 0, -2, -3], [0], [0, -2, -3], [-2, -3]

算法思路

暴力算法就不说了奥，很好想。
这道题与上一道类似，我们可以 使用以下标为 i 结尾的子数组 的方法来解决。但是如何解决判断能否整除呢？？？
这里要使用数学方法辅助：同余定理:
（sum - x）% k == 0 -> sum % k == x % k
这里面sum是当前的前缀和，x 是前面部分数组的前缀和，那么sum - x就可以理解为子数组的和

既然我们要寻找可以被 k 整除的子数组，就只用找到 前面的前缀和 与 当前前缀和 余数一致 的数组，就可以统计数目了：
大体框架与上道题一致
但是有一个细节需要处理 ：C++余数修正
因为数据里有负数，而负数除以一个数的余数在c++中是负数，我们就要对其进行修正，并且还要保证正数的余数正确，所以就要进行一个修正：(sum % k + k) % k 这样就保证了正负数的余数都符合条件了！！！

    int subarraysDivByK(vector<int>& nums, int k) {
        //前缀和 + 哈希优化
        //unordered_map<int , int> hash;
        int hash[10001] = {0};
        hash[0] = 1;
        int count = 0;
        int sum = 0;
        //同余定理 + C++余数修正
        for(auto x : nums)
        {
            sum += x;
            //判断是否可以整除
            //（sum - x）% k == 0 -> sum % k == x % k
            count += hash[(sum % k + k) % k];
            hash[(sum % k + k) % k]++;
        }
        return count ;
    }

提交：过啦！！！

4 Leetcode 525. 连续数组

跟上节奏：525. 连续数组

题目描述

题目很简单，我们需要在给定的数组找到具有相同数量0和1的最长子数组！！！来看样例：

• 输入: nums = [0,1,0]
• 输出: 2
• 说明: [0, 1] (或 [1, 0]) 是具有相同数量0和1的最长连续子数组。

算法思路

暴力算法不在多说，暴力枚举即可。
那么如何使用前缀和来解决问题呢？？？
我们可以将问题转换一下，把数组中的0都变成-1,然后 具有相同数量0和1的最长数组的和就是 0 。这样就转换为和为k的最长子数组。

整体框架与Leetcode 560. 和为 K 的子数组类似，但是如何计算出最长的子数组。先前我们的哈希表储存的是前缀和 -> 个数，我们这道题使用个数肯定不行，而应该是下标位置，而且是距离最远的位置（也就是该前缀和第一次出现的位置）

    int findMaxLength(vector<int>& nums) {
        int ans = 0;
        //前缀和 + 哈希优化
        //细节处理 记录该位置的前缀和
        unordered_map<int ,int> hash1; // 前缀和 -> 最远的位置
        hash1[0] = -1;
        int sum = 0; 
        for(int i = 0 ; i < nums.size(); i++)
        {
        	//0 转换为 -1
            sum += nums[i] == 0 ? -1 : 1;
            //如果哈希表中有 sum 那么直接进行计算
            if(hash1.count(sum)) ans = max(ans , i - hash1[sum]);
            //记录的最远的位置
            else hash1[sum] = i;
            
        }
        return ans;
    }

提交：过啦！！！

5 Leetcode 1314. 矩阵区域和

家人们，上连接：1314. 矩阵区域和

题目描述

这道题乍一看：啥玩意儿，怎么没读懂？！
再一看：嗷嗷！原来如此！

区域和是该题的灵魂，来看样例：

• 输入：mat = [[1,2,3],[4,5,6],[7,8,9]], k = 1
• 输出：[[12,21,16],[27,45,33],[24,39,28]]

我们有一个3 * 3的mat矩阵，所得的ans矩阵也是 3 * 3。
ans矩阵的ans[ i ][ j ]映射到mat矩阵上是 以 mat[ i ][ j ]为中心 ，向四周扩展 k 个区域的矩阵的和。

当然必须保证在扩充后的区域在mat中。

那这样就简单了，就转换为二维前缀和了。我们只需要得到左上角的坐标（x1 ， y1）和右下角的坐标（x2 ， y2）就可以通过公式计算出区域和！！！

我们先来看二维前缀和的预处理如何来做：

这样需要注意一个小细节，我们进行预处理时，把dp矩阵多开一行一列可以极大的简便我们对边界情况的处理！！！

然后就是对ans矩阵进行计算，那么就要找到左上角的坐标（x1 ， y1）和右下角的坐标（x2 ， y2）。
为了保证不出界：

  x1 = max(0, i - k ) + 1;
  y1 = max(0, j - k ) + 1;
  x2 = min((int)ans.size() - 1, i + k ) + 1;
  y2 = min((int)ans[0].size() - 1, j + k ) + 1;

为什么要加 + 1呢？因为我们ans 矩阵没有多开一行一列，为了满足与dp满足映射关系，我们需要进行 + 1！！！

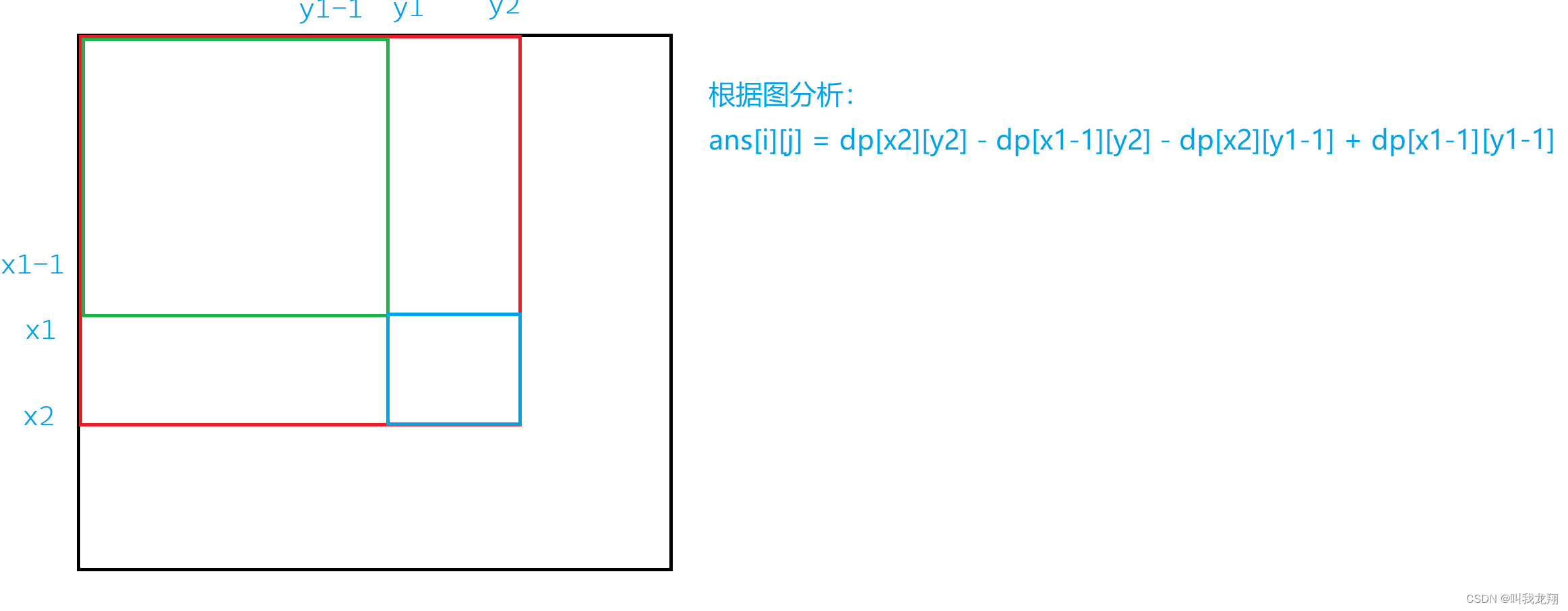
找到两个坐标后，就可以来分析计算区域和了

vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {
    //二维前缀和
    //预处理
    vector<vector<int>> dp(mat.size() + 1, vector<int>(mat[0].size() + 1));
    for (int i = 1; i < dp.size(); i++)
    {
        for (int j = 1; j < dp[0].size(); j++)
        {
            dp[i][j] = dp[i - 1][j] + dp[i][j - 1] + mat[i - 1][j - 1] - dp[i - 1][j - 1];
        }
    }

    vector<vector<int>> ans(mat.size(), vector<int>(mat[0].size()));

    for (int i = 0; i < ans.size(); i++)
    {
        for (int j = 0; j < ans[0].size(); j++)
        {
            //寻找左上角 与 右上角 确保未出界
            int x1, x2, y1, y2;
           x1 = max(0, i - k ) + 1;
           y1 = max(0, j - k ) + 1;
           x2 = min((int)ans.size() - 1, i + k ) + 1;
           y2 = min((int)ans[0].size() - 1, j + k ) + 1;

            ans[i][j] = dp[x2][y2] - dp[x2][y1 - 1] - dp[x1 - 1][y2] + dp[x1 - 1][y1 - 1];
        }
    }
    return ans;

}

提交：过啦!!!

Thanks♪(･ω･)ﾉ谢谢阅读！！！

下一篇文章见