力扣刷题第1天：消失的数字

news2024/12/23 14:14:24

大家好啊，从今天开始将会和大家一起刷题，从今天开始小生也会开辟新的专栏。😜😜😜

第一部分：题目描述

第二部分：题目分析

第三部分：解决方法

3.1 思路一：先排序再查找

3.2 思路二：公式运算

3.3 思路三：异或运算

第四部分：代码实现

第五部分：总结收获

第一部分：题目描述

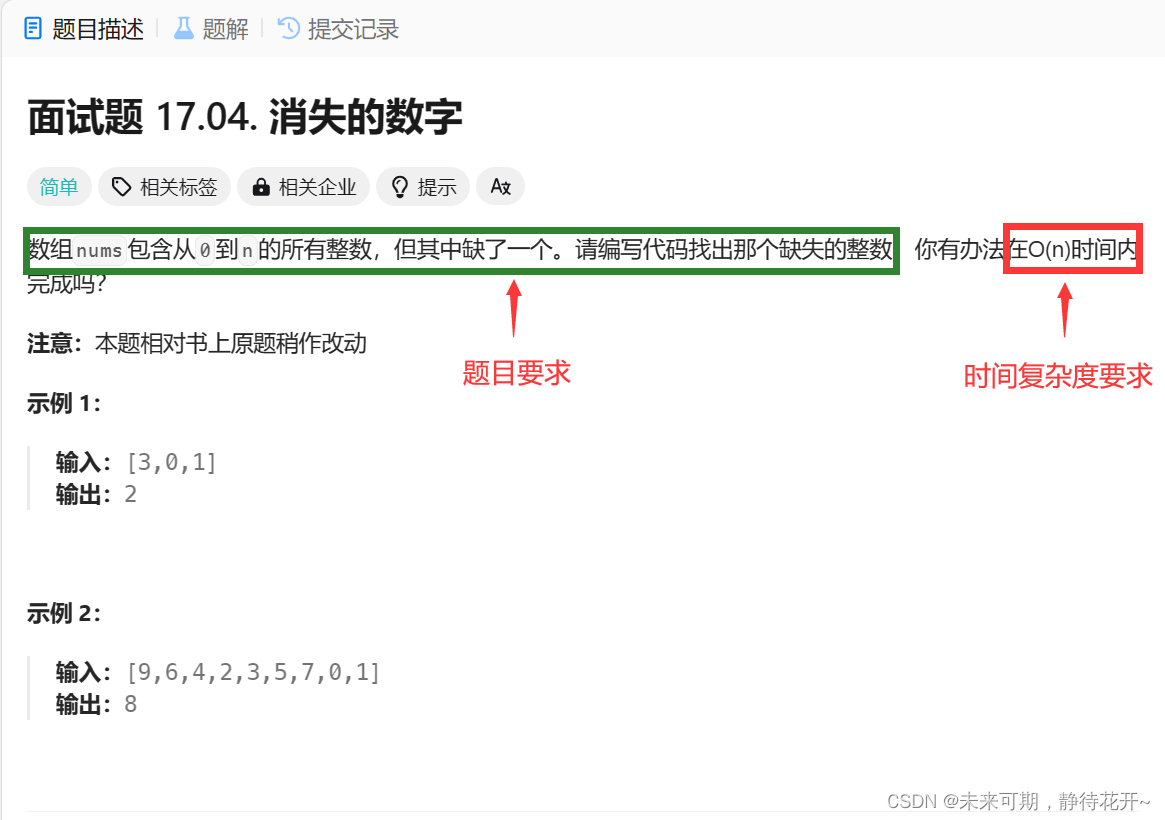
第二部分：题目分析

由图片分析可得，该题目对算法时间复杂度有一定的要求时间复杂度为O(N)，这是关键所在，也就是说只能遍历一遍数组，便可以找到缺失的那个数字。

第三部分：解决方法

3.1 思路一：先排序再查找

既然是0~n内的整数，且仅仅缺少了一个整数，那么我们就可以先对该数组进行排序，再检验相邻下标的元素是否相差为1，理论上便可以得出最后的结果。但是不得不提醒大家，排序的复杂度是相当高的，即便是最复杂度最小的快排，在这个程序内也不合适。我们可以通过图片来认识。

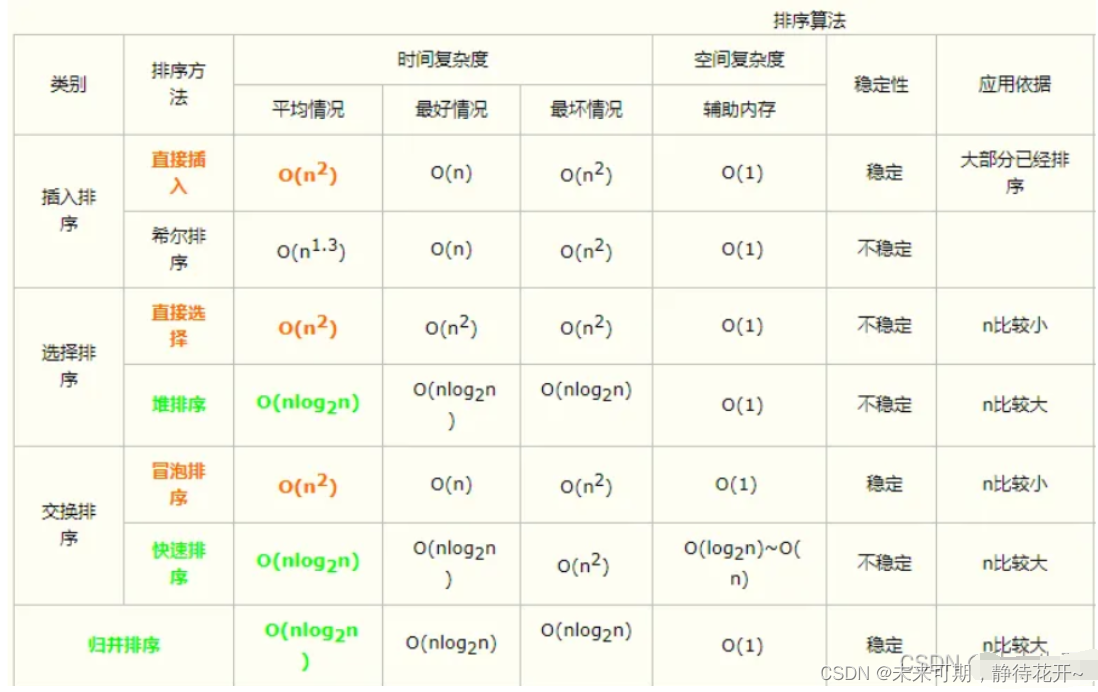
由该表可知，当我们使用效率最高的排序且考虑最坏的情况时，复杂度为N*log(N)，显然在这个题目中超出了复杂度的要求，因此，这种思路虽然是最直接的但是一定会超时。别慌，我们再想想其他办法。

3.2 思路二：公式运算

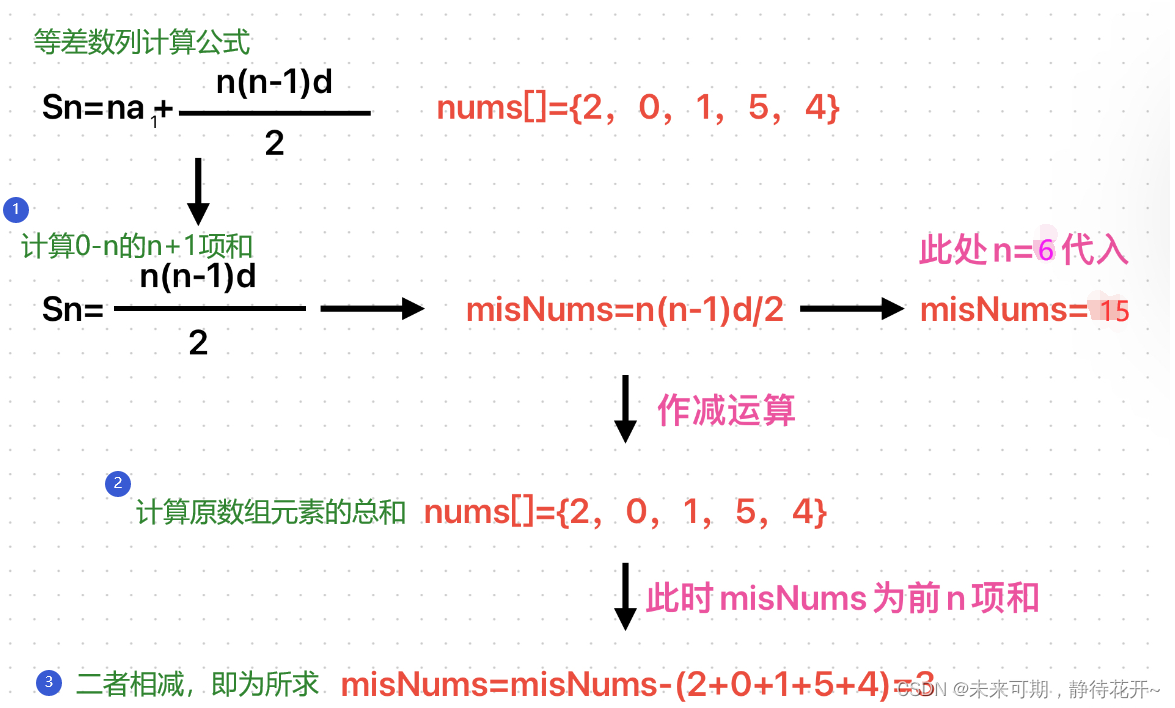
具体问题具体分析，0-n它是一个等差数列，既然我们该数组存储的是0~n里面的整数且只缺少了一个整数，那我们可以用将0 ~ n所有的整数相加，再把该数组中的整数元素相加，最后把这两个相加后的结果相减，便会得到消失的那个数字，直接返回即可。

但是我们可以举一反三，如果题目更改一下，缺失的并非一个数字而是多个数字呢？那这种方法是不是就不起作用啦?这种方法还是不错的，那有没有更加普适性的方法呢？大家可以思考一下。

3.3 思路三：异或运算

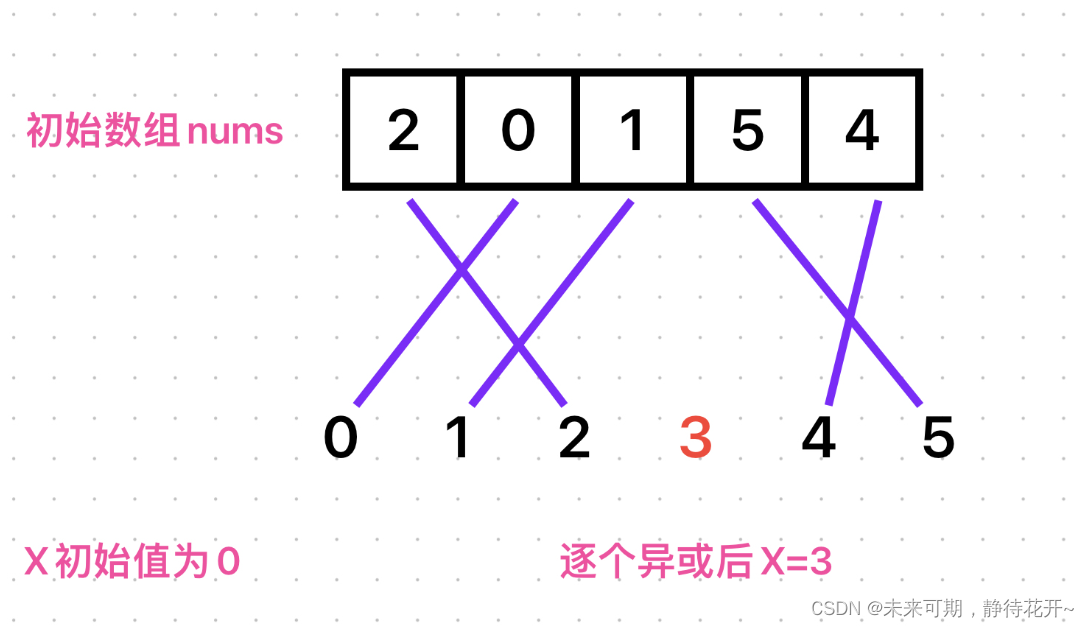
异或运算是属于位运算的一种，它是按照位置进行运算的，位与位异或，相同为0，不相同为1，同时，位运算(按位与、按位或、按位异或)是满足交换律和结合律的，因此，位运算它是没有顺序之分的，改变数的运算顺序，并不会改变最后的结果。

在这道题中，解题的思路在于：两个相同的数异或结果一定是0，0和任何数异或是它本身，因此，我们只需要定义一个初始化为0的变量，依次与该数组每个数字异或，然后和0~n的每一个数字再进行异或，最后留下来的便是所求的数字了。（双爆胎数字异或结果为0，再与其他数异或，并不会改变这个数，最后只剩下单独出现的那个数字，也就是缺失的数字。）

第四部分：代码实现

方法一代码详解：定义两个变量，一个通过循环存储0~n所有数字的和，一个通过循环存储数组所有元素的和，最后相减即可。

注意这里的numSize是数组中的整数的最大取值也就是n, 同时也是数组中的元素个数（数组长度），是通过参数传递的方式进来的。

时间复杂度：O(n)
空间复杂度：O(1)

int Missingnum(int* nums, int numsSize)
{
	int sum1 = 0;
	int sum2 = 0;

   //1.求出0~n所有元素之和
	for (int i = 0; i < numsSize + 1; i++)
	{
		sum1 =sum1+ i;
	}

	//2.求出数组所有元素之和
	for (int j = 0; j < numsSize; j++)
	{
		sum2 =sum2+ nums[j];
	}
	
    //3.直接返回相减的结果
	return sum1 - sum2;
}

方法二代码详解：定义一个初始化为0的变量，依次与该数组（n个元素）和0~n（n+1个元素）的每一个数字异或，最后留下来的便是所求的数字了。

时间复杂度：O(n)
空间复杂度：O(1)

int Missingnum(int* nums, int numsSize)
{
	int tmp = 0;

	//1.依次与数组的每一个元素异或
	for (int i = 0; i < numsSize; i++)
	{
		tmp = tmp ^ nums[i];
	}

	//2.依次与0~n数字异或
	for (int j = 0; j < numsSize +1; j++)
	{
		tmp = tmp ^j;
	}
    
    //3.返回异或的结果
	return tmp;
}