给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：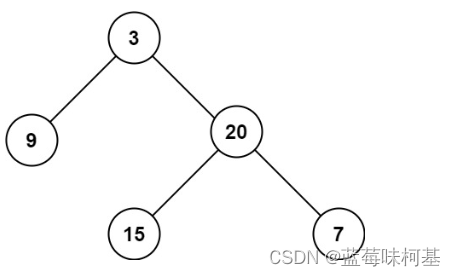
输入：root = [3,9,20,null,null,15,7]
输出：3
示例 2：

输入：root = [1,null,2]
输出：2

提示：

• 树中节点的数量在 [0, 104] 区间内。
• -100 <= Node.val <= 100

题解

• 标签：DFS
• 找出终止条件：当前节点为空
• 找出返回值：节点为空时说明高度为 000，所以返回 000，节点不为空时则分别求左右子树的高度的最大值，同时加 111 表示当前节点的高度，返回该数值
• 某层的执行过程：在返回值部分基本已经描述清楚
• 时间复杂度：O(n)。

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var maxDepth = function(root) {
    if(!root) {
        return 0;
    } else {
        const left = maxDepth(root.left);
        const right = maxDepth(root.right);
        return Math.max(left, right) + 1;
    }
};

以下是网友的图解

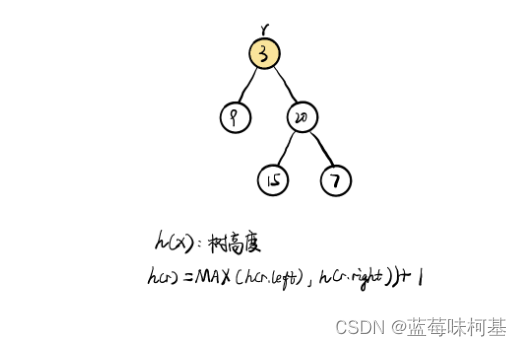
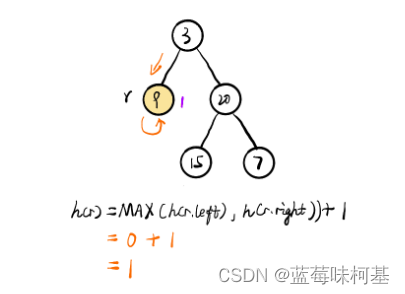
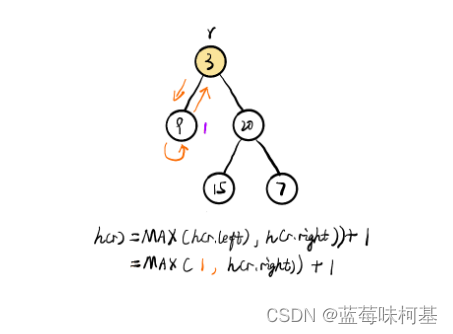
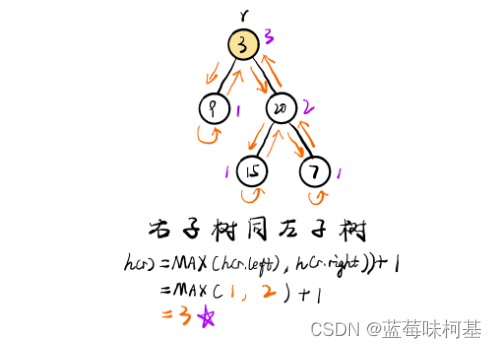
• 首先定义了一个二叉树节点的构造函数 TreeNode，它接受一个参数 val，表示节点的值，并且定义了左子节点 left 和右子节点 right，初始值为 null。
• 函数 maxDepth 接受一个参数 root，表示二叉树的根节点。
• 函数内部使用了递归的方式来计算二叉树的最大深度。
• 如果传入的根节点 root 为 null，即空树，则直接返回深度为 0。
• 如果根节点不为空，则分别递归计算左子树和右子树的最大深度，分别存储在变量 left 和 right 中。
• 最后返回左子树和右子树的最大深度中的较大值，加上 1（因为当前节点也算一层），即为整棵树的最大深度。

DFS

DFS是深度优先搜索（Depth-First Search）的缩写。它是一种用于遍历或搜索树或图的算法。在DFS中，从根节点开始，沿着树的深度尽可能远的路径遍历树，直到遇到叶子节点或者没有未访问过的相邻节点为止。然后回溯到上一个节点，继续探索其他的分支。这个过程一直持续到所有的节点都被访问过为止。
DFS的实现通常使用递归或者栈来维护遍历的顺序。该算法在解决许多图论问题时非常有用，比如查找路径、寻找连通分量等。