每日OJ题_记忆化搜索①_力扣509. 斐波那契数（四种解法）

news2025/1/13 3:11:08

记忆化搜索概念和使用场景

力扣509. 斐波那契数

解析代码1_循环

解析代码2_暴搜递归

解析代码3_记忆化搜索

解析代码4_动态规划

记忆化搜索概念和使用场景

记忆化搜索是一种典型的空间换时间的思想，可以看成带备忘录的爆搜递归。

搜索的低效在于没有能够很好地处理重叠子问题。在搜索过程中，会有很多重复计算，如果我们能记录一些状态的答案，就可以减少重复搜索量。动态规划虽然比较好地处理了重叠子问题，但是在有些拓扑关系比较复杂的题目面前，又显得无奈。记忆化搜索正是在这样的情况下产生的，它采用搜索的形式和动态规划中递推的思想将这两种方法有机地综合在一起，扬长避短，简单实用，在信息学中有着重要的作用。

根据记忆化搜索的思想，它是解决重复计算，而不是重复生成，也就是说，这些搜索必须是在搜索扩展路径的过程中分步计算的题目，也就是“搜索答案与路径相关″的题目，而不能是搜索一个路径之后才能进行计算的题目，必须要分步计算，并且搜索过程中，一个搜索结果必须可以建立在同类型问题的结果上，也就是类似于动态规划解决的那种。

记忆化搜索的典型应用场景是可能经过不同路径转移到相同状态的dfs问题。更明确地说，当我们需要在有层次结构的图（不是树，即当前层的不同节点可能转移到下一层的相同节点）中自上而下地进行dfs搜索时，大概率我们都可以通过记忆化搜索的技巧降低时间复杂度。

动态规划和记忆化搜索都是在爆搜的基础上优化。《算法导论》里也把记忆化搜索看成动态规划。

力扣509. 斐波那契数

509. 斐波那契数

难度简单

斐波那契数 （通常用 F(n) 表示）形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：

F(0) = 0，F(1) = 1
F(n) = F(n - 1) + F(n - 2)，其中 n > 1

给定 n ，请计算 F(n) 。

示例 1：

输入：n = 2
输出：1
解释：F(2) = F(1) + F(0) = 1 + 0 = 1

示例 2：

输入：n = 3
输出：2
解释：F(3) = F(2) + F(1) = 1 + 1 = 2

示例 3：

输入：n = 4
输出：3
解释：F(4) = F(3) + F(2) = 2 + 1 = 3

提示：

0 <= n <= 30

class Solution {
public:
    int fib(int n) {

    }
};

解析代码1_循环

求斐波那契数是很经典的一道题，有多种解法。

下面会从递归解法得出记忆化搜索解法，在得出动态规划解法，循环的解法也可以看作动态规划的状态压缩，完成闭环。

class Solution {
public:
    int fib(int n) {
        if (n < 2)
            return n;
        int fib1 = 0, fib2 = 0, ret = 1;
        for (int i = 2; i <= n; i++)
        {
            fib1 = fib2;
            fib2 = ret;
            ret = fib1 + fib2;
        }
        return ret;
    }
};

解析代码2_暴搜递归

暴搜递归：

递归含义：给 dfs 一个使命，给它一个数 n ，返回第 n 个斐波那契数的值。
函数体：斐波那契数的递推公式。
递归出口：当 n == 0 或者 n == 1 时，不用套公式。

class Solution {
public:
    int fib(int n) {
        return dfs(n);
    }

    int dfs(int n)
    {
        if(n <= 1)
            return n;
        return dfs(n - 1) + dfs(n - 2);
    }
};

解析代码3_记忆化搜索

记忆化搜索：

在递归的基础上加上一个备忘录（所以记忆化搜索也叫带备忘录的递归）。
每次进入递归的时候，去备忘录里面看看。
每次返回的时候，将结果加入到备忘录里面。

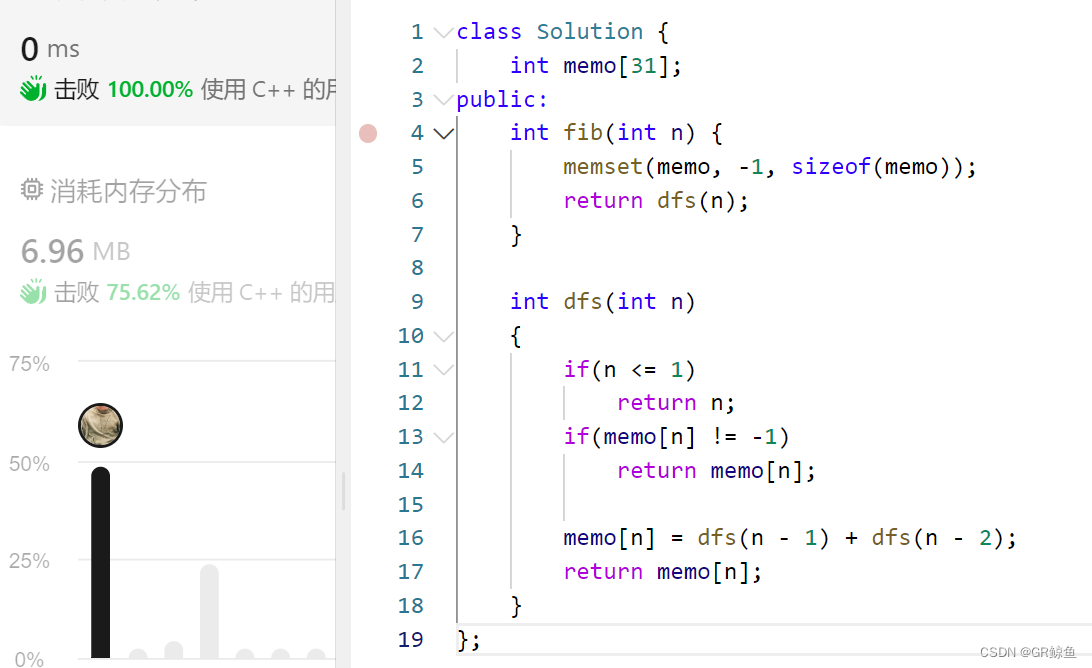
class Solution {
    int memo[31];
public:
    int fib(int n) {
        memset(memo, -1, sizeof(memo));
        return dfs(n);
    }

    int dfs(int n)
    {
        if(n <= 1)
            return n;
        if(memo[n] != -1)
            return memo[n];

        memo[n] = dfs(n - 1) + dfs(n - 2);
        return memo[n];
    }
};

解析代码4_动态规划

动态规划已经写过很多题了，这里根据记忆化搜索得出动态规划的解法：

递归含义：状态表示
函数体：状态转移方程
递归出口：初始化
填表顺序：填备忘录的顺序
返回值：备忘录的值

可以看出都是类似的，因为两者本质都是一样的，都是在爆搜的基础上优化。《算法导论》里也把记忆化搜索看成动态规划。

所以很多时候都可以把爆搜递归的代码改成记忆化搜索，再改成动态规划，不过爆搜改记忆化搜索已经完成时间的优化了，没太多必要改成动态规划了。

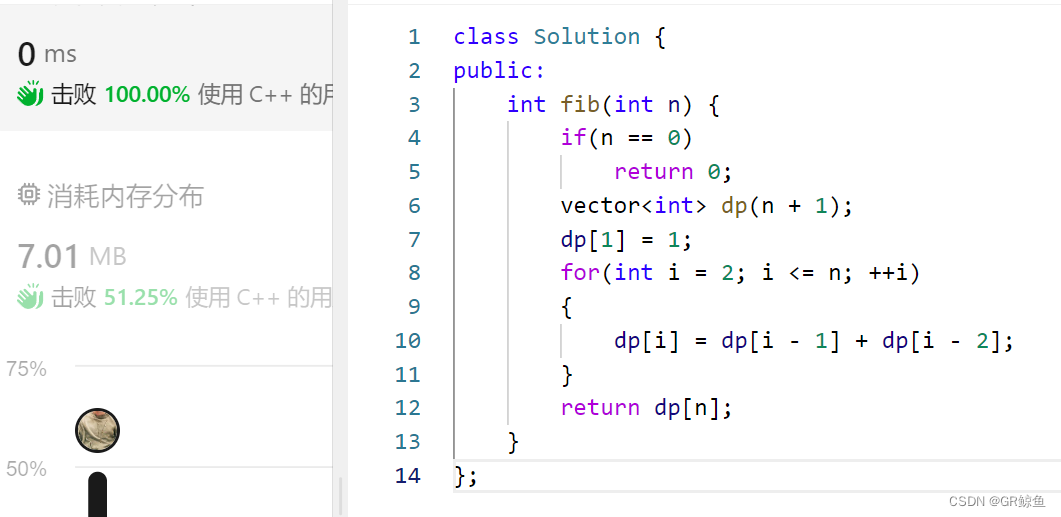
class Solution {
public:
    int fib(int n) {
        if(n == 0)
            return 0;
        vector<int> dp(n + 1);
        dp[1] = 1;
        for(int i = 2; i <= n; ++i)
        {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
};