真题及答案
第一部分数学基础课程
一、(共 5 分)用逻辑符号表达下列语句(论域为包含一切事物的合集)
- (2 分)确诊者并不都有症状(注:需给出两种形式表达, 一种用存在量词, 一种用全称量词)
答:
F(x): x 是确诊者, G(x): x 有症状
∃ x ( F ( x ) ¬ G ( x ) ) ¬ ∀ k ( F ( x ) → G ( x ) ) \begin{array}{l} \exists x(F(x) \neg G(x)) \\ \neg \forall k(F(x) \rightarrow G(x)) \end{array} ∃x(F(x)¬G(x))¬∀k(F(x)→G(x)) - (3 分) 有些老人不喜欢宠物
答:
F(x): x 是老人, G(x): 老人喜欢宠物
∃
x
(
F
(
x
)
¬
G
(
x
)
)
¬
∀
k
(
F
(
x
)
→
G
(
x
)
)
\begin{array}{l} \exists x(F(x) \neg G(x)) \\ \neg \forall k(F(x) \rightarrow G(x)) \end{array}
∃x(F(x)¬G(x))¬∀k(F(x)→G(x))
二、填空题(第 1 小题每空 1 分, 第 2 3 小题每空 2 分, 共 6 分)
- 设集合 A 有 50 个元素, 则由集合 A 可构成__ 2 50 2^{50} 250(2 的 50 次方). \qquad 个子集。其中有 2 49 \qquad 2^{49} 249 (2 的 49 次方) \qquad 个子集其元素个数为奇数。
- 让 5 位中国籍学生和 5 位英国籍学生排成一排, 要求中国籍学生和英国籍学生交叉出现,即同国籍的学生不能相邻, 则有__2*5!*5!___种不同的排法。
- 函数
f
(
x
)
=
(
1
−
3
x
)
−
2
f(x)=(1-3 x)^{-2}
f(x)=(1−3x)−2 中,
x
4
x^4
x4 的系数是_
5
∗
3
4
5 * 3^ 4 \qquad
5∗34
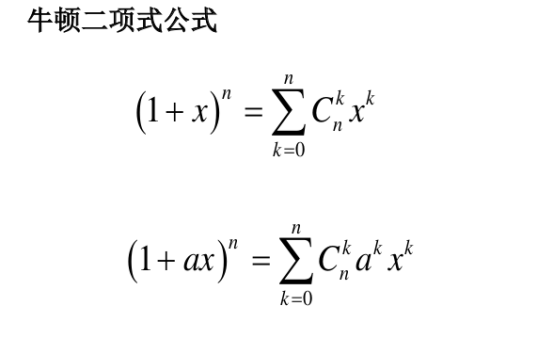

三、计算题 (共 9 分)
- (5 分) 由
P
↑
Q
=
¬
(
P
∧
Q
)
P \uparrow Q=\neg(P \wedge Q)
P↑Q=¬(P∧Q) , 试仅用与非联结词
↑
\uparrow
↑ 分别表示出:
(1) ¬ P \neg P ¬P
(2) P ∧ Q P \wedge Q P∧Q
(2) P → Q P \rightarrow Q P→Q
答:
(1)
¬
P
=
¬
(
P
∧
P
)
=
P
↑
P
\neg P=\neg(P \wedge P)=P \uparrow P
¬P=¬(P∧P)=P↑P
(2)
P
∧
Q
=
¬
(
¬
(
P
∧
Q
)
)
=
(
P
↑
Q
)
↑
(
P
↑
Q
)
P \wedge Q=\neg(\neg(P \wedge Q))=(P \uparrow Q) \uparrow(P \uparrow Q)
P∧Q=¬(¬(P∧Q))=(P↑Q)↑(P↑Q)
(3)
P
→
Q
=
¬
P
∨
Q
=
¬
(
P
∧
¬
Q
)
=
P
↑
(
Q
↑
Q
)
P \rightarrow Q=\neg P \vee Q=\neg(P \wedge \neg Q)=P \uparrow(Q \uparrow Q)
P→Q=¬P∨Q=¬(P∧¬Q)=P↑(Q↑Q)
- (4 分) 对任意正整数
n
⩾
2
n \geqslant 2
n⩾2 , 给出
C
(
n
,
1
)
+
C
(
n
,
2
)
+
…
+
(
C
n
,
n
)
C(n, 1)+C(n, 2)+\ldots+(C n, n)
C(n,1)+C(n,2)+…+(Cn,n) 的最简表达式(即计算其值),其中
C
(
n
,
i
)
C(n, i)
C(n,i) 表示从 n 个元素中取 i 个元素的组合数。
答:
( 1 + x ) n = C ( n , 0 ) + C ( n , 1 ) + C ( n , 2 ) + … + ( C n , n ) (1+x)^n=C(n, 0)+C(n, 1)+C(n, 2)+\ldots+(C n, n) (1+x)n=C(n,0)+C(n,1)+C(n,2)+…+(Cn,n)
令 x=1 得,
( 1 + 1 ) n = C ( n , 0 ) + C ( n , 1 ) + C ( n , 2 ) + … + ( C n , n ) = 2 n (1+1)^n=C(n, 0)+C(n, 1)+C(n, 2)+\ldots+(C n, n)=2^n (1+1)n=C(n,0)+C(n,1)+C(n,2)+…+(Cn,n)=2n
则 C ( n , 1 ) + C ( n , 2 ) + … + ( C n , n ) = 2 n − C ( n , 0 ) = 2 n − 1 C(n, 1)+C(n, 2)+\ldots+(C n, n)=2^n-C(n, 0)=2^n-1 C(n,1)+C(n,2)+…+(Cn,n)=2n−C(n,0)=2n−1
四、解答题(共 2 小题,每小题 5 分,共 10 分)
- 由 2,4,6,8 (数字可重复使用) 这四个数字组成的 n 位数中 ( n ⩾ 2 ) (n \geqslant 2) (n⩾2) 要求含偶数个 2 ,奇数个 4 且至少含 1 个 6 , 数字 8 出现的次数不加限制。设满足这些条件的 n \mathrm{n} n 位数的个数为 a n a^n an。
(1)求 a1, a2, a3…, an…对应的指数型母函数 g(x) 。
(2)求 an 的表达式。
答:
(1) 满足题目要求的指数型母函数为
g
(
x
)
=
(
x
+
x
3
3
!
+
⋯
)
(
1
+
x
2
2
!
+
x
4
4
!
+
⋯
)
(
x
+
x
2
2
!
+
x
3
3
!
+
⋯
)
(
1
+
x
+
x
2
2
!
+
x
3
3
!
+
⋯
)
=
(
e
x
−
e
−
x
2
)
(
e
x
+
e
−
x
2
)
(
e
x
−
1
)
e
x
=
1
4
(
e
4
x
−
e
3
x
+
e
−
x
−
1
)
=
1
4
∑
n
=
0
∞
(
4
n
−
3
n
+
(
−
1
)
n
)
x
n
n
!
−
1
4
\begin{aligned} & \mathrm{g}(\mathrm{x})=\left(x+\frac{x^{3}}{3!}+\cdots\right)\left(1+\frac{x^{2}}{2!}+\frac{x^{4}}{4!}+\cdots\right)\left(x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\cdots\right)\left(1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\cdots\right) \\ = & \left(\frac{e^{x}-e^{-x}}{2}\right)\left(\frac{e^{x}+e^{-x}}{2}\right)\left(e^{x}-1\right) e^{x}=\frac{1}{4}\left(e^{4 x}-e^{3 x}+e^{-x}-1\right) \\ = & \frac{1}{4} \sum_{n=0}^{\infty}\left(4^{n}-3^{n}+(-1)^{n}\right) \frac{x^{n}}{n!}-\frac{1}{4} \end{aligned}
==g(x)=(x+3!x3+⋯)(1+2!x2+4!x4+⋯)(x+2!x2+3!x3+⋯)(1+x+2!x2+3!x3+⋯)(2ex−e−x)(2ex+e−x)(ex−1)ex=41(e4x−e3x+e−x−1)41n=0∑∞(4n−3n+(−1)n)n!xn−41
(2) 由 (1) 知,
a n = 1 4 ( 4 n − 3 n + ( − 1 ) n ) a_{n}=\frac{1}{4}\left(4^{n}-3^{n}+(-1)^{n}\right) an=41(4n−3n+(−1)n)
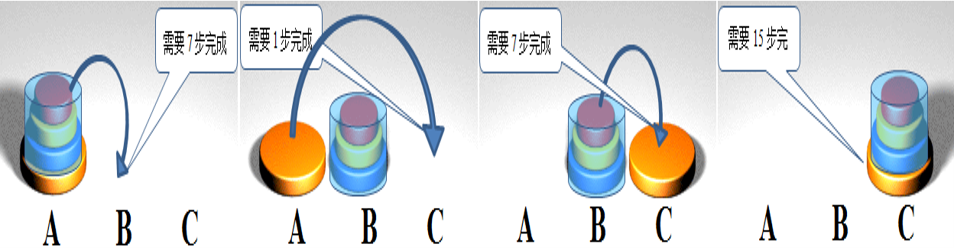
- 有 5 个人雨天带伞参加会议, 每人带一把伞, 进入会场时随意放伞, 结束时每人随意拿一把伞离开,问:
( 1 )每人拿到的都不是自己的伞的排列数。
(2)至少有一人拿到自己伞的概率是多少?
答:
(1)
设 1 个人拿回自己雨伞的排列数为 |A i| , 其中 i=1,2,3,4,5
则 |A i|=
4
!
∣
4!\mid
4!∣
设 2 个人拿回自己雨伞的排列数为 |A i j| , 其中 i, j=1,2,3,4,5
则 |A i j|=3 !
以此类推,
3 个人拿回自己雨伞的排列数为 |A i j k|=2!
4 个人拿回自己雨伞的排列数为 |A i j k h|=1 !
5 个人拿回自己雨伞的排列数为
∣
A
i
j
k
h
∣
∣
=
1
|A i j k h| \mid=1
∣Aijkh∣∣=1
根据容斥原理, 每个人拿回的都不是自己的伞的排列数
S
\mathrm{S}
S 为,
S
=
5
!
−
C
(
5
,
1
)
∗
4
!
+
C
(
5
,
2
)
∗
3
!
−
C
(
5
,
3
)
∗
2
!
+
C
(
5
,
4
)
∗
1
!
−
1
=
44
\begin{array}{l} S= \\ 5!-C(5,1) * 4!+C(5,2) * 3!-C(5,3) * 2!+C(5,4) * 1!-1 \\ =44 \end{array}
S=5!−C(5,1)∗4!+C(5,2)∗3!−C(5,3)∗2!+C(5,4)∗1!−1=44
即每个人拿回的都不是自己的伞的排列数为 44
(2)至少有一个人拿回自己雨伞的排列数 S 1 为,
S
1
=
5
!
−
S
=
120
−
44
=
76
S 1=5!-S=120-44=76
S1=5!−S=120−44=76
则至少一个人拿回自己雨伞的概率为 ( 76 / 120 ) ∗ 100 % ≈ 63.33 % (76/120)*100\% \approx 63.33 \% (76/120)∗100%≈63.33%
另一种解法
解:
(1) 5 人错位排序
D
5
=
∣
A
ˉ
1
∩
A
ˉ
2
∩
A
ˉ
3
∩
A
ˉ
4
∩
A
ˉ
5
∣
=
5
!
⋅
(
1
−
1
1
!
+
1
2
!
−
1
3
!
+
1
4
!
−
1
5
!
)
=
44
\begin{array}{l} D_{5} \\ \end{array}=\left|\bar{A}_{1} \cap \bar{A}_{2} \cap \bar{A}_{3} \cap \bar{A}_{4} \cap \bar{A}_{5}\right|=5!\cdot\left(1-\frac{1}{1!}+\frac{1}{2!}-\frac{1}{3!}+\frac{1}{4!}-\frac{1}{5!}\right)=44
D5=
Aˉ1∩Aˉ2∩Aˉ3∩Aˉ4∩Aˉ5
=5!⋅(1−1!1+2!1−3!1+4!1−5!1)=44
即 全排列数减去 5 人错排的概率,为:
1
−
D
5
5
!
≈
0.632
1-\frac{D_{5}}{5!} \approx 0.632
1−5!D5≈0.632
或从另一个角度考虑,即5人中最多有四人错排,
其概率为
11
−
1
2
!
+
1
3
!
−
1
4
!
+
1
5
!
≈
0.632
1 1 -\frac{1}{2!}+\frac{1}{3!}-\frac{1}{4!}+\frac{1}{5!} \approx 0.632
11−2!1+3!1−4!1+5!1≈0.632
拓展: 至少 2 人拿到自己原伞的概率
1
2
!
−
1
3
!
+
1
4
!
−
1
5
!
\frac{1}{2!}-\frac{1}{3!}+\frac{1}{4!}-\frac{1}{5!}
2!1−3!1+4!1−5!1

五、证明题
1、设
A
\mathrm{A}
A 是包含
n
\mathrm{n}
n 个元素的有限集,
R
\mathrm{R}
R 是
A
\mathrm{A}
A 上的关系,则必存在
s
\mathrm{s}
s 和
t
\mathrm{t}
t ,使得
R
s
=
R
t
R^{s}=R^{t}
Rs=Rt ,并且
0
≤
s
<
t
≤
2
n
2
0 \leq s<t \leq 2^{n^{2}}
0≤s<t≤2n2 。
解析:【定理】设 A \mathrm{A} A 为含有 n \mathrm{n} n 个元素的有穷集 R ⊆ A × A R \subseteq A \times A R⊆A×A ,则存在自然数s, t \mathrm{t} t , 且满足 0 ≤ s < t ≤ 2 n 2 0 \leq s<t \leq 2^{n^{2}} 0≤s<t≤2n2 , 使得 R s = R t R^{s}=R^{t} Rs=Rt 。
显然 P ( A × A ) P(A \times A) P(A×A) 中元素对幂运算是封闭的,即对任意的自然数 k \mathrm{k} k ,有 R k ∈ P ( A × A ) , k = 0 , 1 , 2 , … P ( A × A ) R^{k} \in P(A \times A), k=0,1,2, \ldots P(A \times A) Rk∈P(A×A),k=0,1,2,…P(A×A)
的二元关系,由鸽巢原理可知,存在s, , 满足
0
≤
s
<
t
≤
2
n
2
0 \leq s<t \leq 2^{n^{2}}
0≤s<t≤2n2 ,使得
R
s
=
R
t
R^{s}=R^{t}
Rs=Rt 。

- 设 k \mathrm{k} k 是简单图 G \mathrm{G} G 的顶点度数的最小值,证明G包含一条长度至少为 k 的路。
解析: 用反证法,假设最长路的长度 l ≤ k − 1 l \leq k-1 l≤k−1 ,即从 v 0 v_{0} v0 到 v l v_{l} vl 的长度为 l 。
由题干可知 d ( v 0 ) ≥ k d\left(v_{0}\right) \geq k d(v0)≥k , 则 G \mathrm{G} G 中至少有 k \mathrm{k} k 个点与 v 0 v_{0} v0 有边相连,而假设中 v 0 v_{0} v0 链接最长路的长度 l ≤ k − 1 l \leq k-1 l≤k−1 ,则一定有另一个点与 v 0 v_{0} v0 相连且在 l 外,则假设相矛盾,因此 l ≥ k l \geq k l≥k ,等证。
简单无向图(不存在顶点到自身的边,且任意两个不同的顶点之间没有平行的两条边),简单有向图(不存在顶点到自身的弧,且任意两个不同的顶点之间没有同方向 的两条弧)。简单无向图和简单有向图统称为简单图。
第二部分计算机网络
一、填空题
-
以太网采用 截断二进制指数退避 算法来确定碰撞后重传的时间, 当第 3 次发生碰撞后,节点随机从 { 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 } \{0,1,2,3,4,5,6,7\} \quad {0,1,2,3,4,5,6,7} 中间选择一个值。

-
某计算机的 IP 地址为 168.35.110.2, 子网掩码为 255.255.224.0, 则该计算机的子网地址为_168.35.96.0_; 与掩码对应的网络前缀有 19 位。
-
考虑在主机 A 和主机 B 之间建立一个 T C P 连接, 若主机 A 向主机 B 连续发送两个 TC P 报文段, 第一个报文段的序号为 90 , 第二个报文段的序号为 110 , 则第一个报文段中的数据为 20 字节。若第一个报文段丢失, 第二个报文段达到主机 B \mathrm{B} B , 主机 B \mathrm{B} B 发送的报文确认号为 90 .
二、选择题(共 5 分)
1 IP 地址为 10.23.10.0/10, 那么在该网络里的正确的 IP 地址是()
A. 10.23 .130 .2
B. 10.23 .200 .1
C. 10.23 .58 .8
D . 10.23 .128 .0
答: C
2 . 一台主机的 IP 地址为 130.68.80.12, 子网掩码为 255.255.192.0, 必须通过路由器才能和该主机通信的是()
A. 130.68 .67 .15
B. 130.68 .85 .220
C. 130.68 .62 .23
D. 130.68 .90 .30
答: C
3 . 用户甲发送消息给用户乙,如果既需要提供认证功能,又要保证被发送消息的保密性,可采用的方法是()。
A. 发送方用其私钥对消息进行数字签名和加密
B. 发送方用接收方的公钥进行数字签名和加密
C. 发送方先用其私钥对消息进行数字签名,然后再用接收方的公钥加密
D. 发送方先用接收方的公钥进行数字签名, 然后再用自己的私钥进行加密答: C
- TCP 的下列说法中, 错误的是()
A. TCP 以报文段为单位组织
B. TCP 以消息为单位向应用层传送数据
C. TCP 是面向字节流的
D. TCP…
答: B
5. 数据链路层的功能, 错误的是()
A. 差错控制
B. 帧同步
C. 数据分组和组装
D. 透明传输
答: A
数据链路层最基本的服务是将源计算机网络层来的数据可靠的传输到相邻节点的目标计算机的网络层。为达到这一目的,数据链路层必须具备一系列相应的功能,主要有:如何将数据组合成数据块(在数据链路层中将这种数据块称为帧,帧是数据链路层的传送单位);如何控制帧在物理信道上的传输,包括如何处理传输差错,如何调节发送速率以使之与接收方相匹配;在两个网路实体之间提供数据链路通路的建立、维持和释放管理。
https://yueliusu.blog.csdn.net/article/details/124768543?spm=1001.2101.3001.6661.1&utm_medium=distribute.pc_relevant_t0.none-task-blog-2%7Edefault%7EBlogCommendFromBaidu%7ERate-1-124768543-blog-105125423.235%5Ev43%5Epc_blog_bottom_relevance_base8&depth_1-utm_source=distribute.pc_relevant_t0.none-task-blog-2%7Edefault%7EBlogCommendFromBaidu%7ERate-1-124768543-blog-105125423.235%5Ev43%5Epc_blog_bottom_relevance_base8&utm_relevant_index=1
三、名词解释
1.CIDR
答:
CIDR全称无分类域间路由,是解决IP地址短缺的好方法,消除了传统ABCDE类的划分,用IP地址/前缀表示,前缀用来指明网络,后缀用来指明主机。CIDR把前缀都相同的连续的IP地址组成了一个CIDR地址块。IP的分配都以CIDR地址块为单位。
2. 网络地址转换NAT
答:
网络地址转换NAT(Network addresstranslation),专用网内部使用专用IP地址,仅在连接到因特网的路由器使用全球IP地址,大大节约了宝贵的IP地址
- 需要在路由器上安装NAT软件,装有NAT软件的路由器叫NAT路由器,它至少拥有一个全球IP地址
- 本地地址与全球IP地址进行转换
- 若NAT拥有n个全球IP地址,则专用网内最多可以同时有n个主机接入到因特网
- NAT路由器的通信必须由专用网内的主机发起,因此专用网内的主机不能当作服务器用
- 为了更有效的利用NAT路由器上的全球IP地址,常用的NAT转换表把运输层的端口号也利用上了,使用端口号的NAT也叫NAPT
- 普通路由器转发时,不改变源IP地址跟目的IP地址,NAT路由器转发时,一定要更换IP地址
四、问答与计算(1G≈10^9, 1M≈10^6, 1K≈10^3 )
1. 两台主机之间通过长距离网络通信,彼此之间通过一条传输速率为1Gbps 的信道相连。往返传播时延为30毫秒。分组(包括头部和数据字段)长度为1500字节。
(1)如果采用停等协议,信道的利用率是多少?
(2)若设计一个回退N(Go-back-n)滑动窗口协议,使信道的利用率达到70%,窗口大小应为多少?
答:
(1)每个分组的发送时延1500*8/10^9 = 0.012ms
信道的利用率0.012/(0.012+30) ≈0.04%
(2)设窗口大小为N,根据题意:
0.012
×
N
/
(
0.012
+
30
)
≥
70
0.012×N/(0.012+30)≥70%
0.012×N/(0.012+30)≥70,解得N≥1750.7,即N最小为1751

https://blog.csdn.net/zxz947462113/article/details/132814271
第四部分软件工程
一、单项选择题(每小题1分,共5分)
- 一个模块内部的各部分没什么联系,另一个模块通过传递基本参数向它传递一个控制,该模块属于什么()内聚
A.数据内聚
B.逻辑内聚
C.通信内聚
D.顺序内聚
答:B
逻辑内聚:指模块内执行若干个逻辑上相似的功能,通过参数确定该模块完成哪一个功能。例如:将功能上相似的模块 B 、 C 、 D ,放在一个模块中,模块 A 需要用不同的参数去调用具体的模块去完成相应的功能。相当于进行次判断。
2.DFD顶层流图用于指出系统的()
A.数据主体
B.数据存储
C.输入与输出
D.处理过程
答:C
3.黑盒测试主要考虑系统的()
A.程序流程
B.功能
C.判定分支结构
D.异常处理
答:B
4. RUP中的“谁做”,“怎么做”,“做什么”里的“谁做”有哪个概念/术语()完成
A.制品
B.角色
C.工作流
D.数据
答:B
RUP应用了角色、活动、制品和工作流4种重要的模型元素。其中角色表述“谁做”,制品
表述“做什么”,活动表述“怎么做”,工作流表述“什么时候做”。
角色:RUP预先定义了许多角色,角色描述了在项目开发中,一个人或者一个开发团队的工作职能与任务。 [1]
活动:它是一个有明确功能的独立模块,反映了系统的某个功能。
工件:是在活动进行过程中产生、创建或修改的一段信息,同时也是项目开发的文档资料。
- 面向对象设计模式,说法正确的是()
A.使程序员能够更快的完成
B.可以复用好的设计
C.使程序以最快的速度
D.…
答:B
二、判断题(每小题1分,共5分)
-
CMMI是过程改进模型,它支持阶段性过程改进不支持连续性过程改进()
答:错
CMMI全称是能力成熟度模型集成,CMMI认证一共有5个级别,CMMI1级,完成级;CMMI2级,管理级;CMMI3级,定义级;CMMI4级,量化管理级;CMMI5级,优化级。 -
某项目组织打算开发一个大型系统,且具备了相关领域知识以及开发经验,此时采用瀑布模型是最好的选择()
答:对 -
采用UML进行软件设计时,可用依赖关系表示两类事物的“整体/部分”关系()
采用UML进行软件设计时,可用____泛化__关系表示两类事物之间存在的特殊/一般关系,用聚集关系表示事物之间存在的整体/部分关系。 答:错
4.质量控制不是软件配置管理活动()
答:对
软件配置管理的活动主要有编制配置管理计划、配置标识、配置控制、配置状态报告、配置评价、发行管理和交付。
5. 风险预测从两个方面,即风险发生的可能性跟风险消除方法()
答:错
①风险发生的可能性或概率,即 评估风险概率 ;②风险发生所产生的后果,即 评估风险影响 。
三、简答题(共12分)
1. 什么是开源软件?试举一简单说明。
答:
开源软件(open-source)是一个新名词,它被定义为描述其源码可以被公众使用的软件,并且此软件的使用,修改和分发也不受许可证的限制。开放源码软件通常是有copyright的,它的许可证可能包含这样一些限制:蓄意的保护它的开放源码状态,著者身份的公告,或者开发的控制。“开放源码”正在被公众利益软件组织注册为认证标记,这也是创立正式的开放源码定义的一种手段。
如GitHub
2.RUP的每一个迭代周期中设计6个核心工程工作流,3个核心支持工作流。试简述每个核心工程工作流的名称和主要目的。
答:
1)商业建模(BusinessModeling)
商业建模工作流描述了如何为新的目标组织开发一个构想,并基于这个构想在商业用例模型和商业对象模型中定义组织的过程,角色和责任。
2)需求(Requirements)
需求工作流的目标是描述系统应该做什么,并使开发人员和用户就这一描述达成共识。为了达到该目标,要对需要的功能和约束进行提取、组织、文档化;最重要的是理解系统所解决问题的定义和范围。
3)分析和设计(Analysis& Design)
分析和设计工作流将需求转化成未来系统的设计,为系统开发一个健壮的结构并调整设计使其与实现环境相匹配,优化其性能。分析设计的结果是一个设计模型和一个可选的分析模型。设计模型是源代码的抽象,由设计类和一些描述组成。设计类被组织成具有良好接口的设计包(Package)和设计子系统(Subsystem),而描述则体现了类的对象如何协同工作实现用例的功能。设计活动以体系结构设计为中心,体系结构由若干结构视图来表达,结构视图是整个设计的抽象和简化,该视图中省略了一些细节,使重要的特点体现得更加清晰。体系结构不仅仅是良好设计模型的承载媒介,而且在系统的开发中能提高被创建模型的质量。
4)实现(Implementation)
实现工作流的目的包括以层次化的子系统形式定义代码的组织结构;以组件的形式(源文件、二进制文件、可执行文件)实现类和对象;将开发出的组件作为单元进行测试以及集成由单个开发者(或小组)所产生的结果,使其成为可执行的系统。
5)测试(Test)
测试工作流要验证对象间的交互作用,验证软件中所有组件的正确集成,检验所有的需求已被正确的实现,识别并确 认缺陷在软件部署之前被提出并处理。RUP提出了迭代的方法,意味着在整个项目中进行测试,从而尽可能早地发现缺陷,从根本上降低了修改缺陷的成本。测试类似于三维模型,分别从可靠性、功能性和系统性能来进行。
6)部署(Deployment)
部署工作流的目的是成功的生成版本并将软件分发给最终用户。部署工作流描述了那些与确保软件产品对最终用户具有可用性相关的活动,包括:软件打包、生成软件本身以外的产品、安装软件、为用户提供帮助。在有些情况下,还可能包括计划和进行beta测试版、移植现有的软件和数据以及正式验收。
3. 结构化程序设计方法要求再复杂的程序结构也应使用基本控制结构组合嵌套来实现。试问这些基本控制结构有哪些?并试用类C语言或程序流程图简单描述。
答:
结构化程序设计的基本控制结构有选择结构,顺序结构,循环结构,每一个结构只有一个入口和出口。
四、建模题(共8分)
在学校的教学管理系统中,学生查询成绩就是系统中的一次交互行为。问题陈述如下:
开始时终端上显示首页,用户选择“查询”请求后,显示“请输入学号”。
在用户输入学号后,系统查询学生文件,和对学生学号:若输入的学号不正确,则显示“输入学号不正确”,此次查询取消,回到首页;若输入正确,出现“请输入课程名”。
一旦输入课程名,则开始查找课程文件:若输入的课程名不正确,则显示“输入的课程名不正确”,此次查询取消,回到首页;若输入正确,则根据“学号”和“课程名”查询选课文件。
若在选课文件中查询成功,显示查询到的成绩,当用户选择“继续查询”后回到“请输入学号”,当用户选择“结束查询”后回到首页。若查询失败,则显示“查询失败”后回到首页。
1. (5分)下图时该系统的状态图,其中有5个状态的名字缺失,请补充完整。
2. (3分)计算途中的McCabe环路复杂度,并依据基本路径覆盖原则确定可能的测试路径。
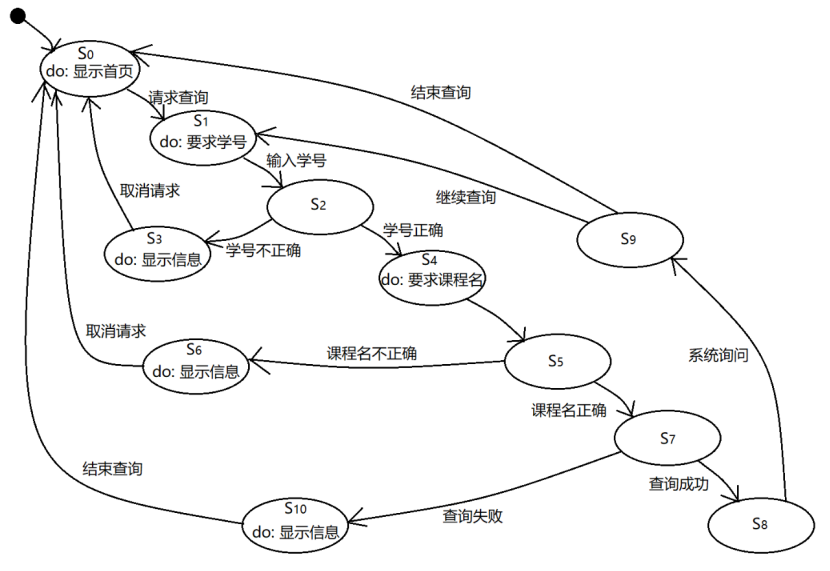
答:
(1)S2: do:核对学号
S5: do: 核对课程名
S7: do: 查询选课文件
S8: do: 显示成绩
S9: do: 要求用户输入
(2)
环路复杂度为5
基本路径覆盖原则包括路径覆盖、条件组合覆盖、条件覆盖、分支覆盖、语句覆盖等。根据分支覆盖原则,可能的测试路径包括:
a.S0→S1→S2→S→S0
b.S0→S1→S2→S4→S5→S6→S0
c.S0→S1→S2→S4→S5→S7→S10→S0
d.S0→S1→S2→S4→S5→S7→S8→S9→S0
e.S0→S1→S2→S4→S5→S7→S8→S9→S1