A题多个火箭残骸的准确定位：

A题已经更新完22页完整版论文＋高清无水印照片＋Python（MATLAB）代码
简单麦麦https://www.jdmm.cc/file/2710544/

问题1：单个残骸的音爆位置确定

建模思路：

1. 声波传播模型：首先，需要了解声波在空气中的传播速度固定（340 m/s），通过测量声波到达不同设备的时间差，可以估计声源的位置。

2. 几何定位：最少需要三个监测设备来在三维空间中定位一个点。这可以通过解三维空间中的多个球面方程来实现，每个球的中心是一个监测设备，半径是声波传播距离。

3. 最小二乘法：由于可能存在测量误差，可以用最小二乘法来优化估计的音爆位置。

计算步骤：

1. 将经度和纬度转换为笛卡尔坐标系下的x，y坐标。

2. 对于每个设备，计算其与声源的距离

3. 利用多个数据组成的方程组通过数值方法求解位置 （x，y，z）

问题2：多个残骸的音爆位置确定

建模思路：

1. 数据关联：首先需要确定每个设备接收到的震动波分别来自哪一个残骸。这可以通过比较不同设备收到的音爆时间差进行初步关联。

2. 多目标跟踪：使用如多假设跟踪（MHT）或联合概率数据关联（JPDA）等算法来处理多个目标的跟踪问题。

3. 设备数量决定：理论上，每个残骸的定位至少需要三个设备，因此四个残骸至少需要十二个设备（每个残骸三个独立设备），但实际中可以共享设备。

问题3：具体数据的应用与模型验证

1. 利用问题2中的模型，对表中数据进行处理，关联每个时间戳对应的残骸。

2. 通过解相应的几何定位方程，确定每个残骸的具体位置和时间。

问题4：误差分析和修正模型

建模思路：

1. 随机误差模型：引入高斯噪声来模拟设备记录时间的误差。

2. 误差传播分析：分析时间记录误差如何影响最终的空间定位误差。

3. 优化方案：考虑使用滤波器，如卡尔曼滤波器，来减少误差影响。

实施步骤

1. 在问题3的数据基础上添加随机误差。

2. 重复问题3的定位过程，记录位置误差。

3. 分析误差结果，并探讨如何通过算法优化减少误差。

B题已经更新完42页完整版论文＋高清无水印照片＋Python（MATLAB）双代码

简单麦麦https://www.jdmm.cc/file/2710617/

B题：批量工件并行切割下料问题

板材利用率、设备时间管理以及成本控制的复杂工程优化

问题一：板材切割排版方案

建模思路

1. 几何排布优化：将工件切割下料问题视为一个二维装箱问题（2D bin packing），目标是最大化板材面积利用率。

2. 启发式算法：使用启发式算法，如最佳适应算法（Best Fit），先进优先搜索（Best First Search）或遗传算法等，进行工件的排列组合。

3. 约束条件：保证每块板材至少包含5种型号的工件，同时考虑工件间和板边的最小间距。

操作步骤

· 将工件按大小、形状分类并优先排列较大的工件，以减少空间碎片。

· 考虑旋转工件以适应板材形状，以提高利用率。

问题二：并行切割下料时间优化

建模思路

1. 调度优化：此问题为多机调度问题，需优化刀具和轨道的运动以最小化总切割时间。

2. 冲突避免：确保刀具间不会发生冲突，并考虑刀具的最小间隔约束。

3. 动态规划或搜索算法：应用动态规划或启发式搜索算法，比如A*搜索，优化刀具和轨道的运行路径。

操作步骤

· 设计一个轨道和刀具的协同运行方案，包括刀具的升起和恢复切割操作。

· 模拟刀具的切割路径，以及轨道的移动，优化整体操作时间。

问题三：板材组合切割下料

建模思路

1. 多目标优化：在保证高板材利用率的前提下，选择合适数量和类型的板材进行组合切割。

2. 整数规划：使用整数线性规划模型来确定每种板材的最优数量。

C题-编译器版本的识别问题保姆级思路＋代码

简单麦麦https://www.jdmm.cc/file/2710546/

问题1：使用GCC中不同版本的C++编译器编译程序源代码，并对比编译结果

1. 编译实验：选择几个不同版本的GCC C++编译器，使用默认编译选项对给定的程序源代码进行编译。
2. 结果对比：对编译后的机器代码或汇编代码进行对比，寻找差异。
3. 特征提取：识别出编译结果中的差异点，这些差异点可能包括但不限于：
   1. 优化级别不同导致的差异
   2. 新版本引入的新特性或指令集
   3. 错误修正或安全性改进
4. 文档记录：详细记录每个版本编译器的编译选项、编译时间和编译结果的差异。

问题2：构造判别函数

1. 特征选择：从问题1中提取的特征里选择最有区分力的特征。
2. 函数设计：设计一个函数或算法，该函数能根据编译结果的特征来预测编译器的版本。
3. 模型训练：使用问题1中的编译结果数据来“训练”判别函数，调整参数以提高准确性。
4. 验证测试：使用一部分未参与训练的数据来测试判别函数的性能。

问题3：使用判别函数区分编译器版本

1. 编译新代码：使用附件2中的源程序代码，用不同版本的GCC C++编译器进行编译。
2. 应用判别函数：将问题2中得到的判别函数应用于新编译的代码结果。
3. 结果分析：分析判别函数的输出，确定其准确性和可靠性。
4. 泛化能力研究：探讨判别函数对不同类型源代码的适用性。

问题3:为了评估问题2训练得到的分类器模型,需要在新的测试集上进行泛化性

能分析。附件2的源代码可以作为一个测试用例。首先,用不同编译器版本编译

该代码,得到一批测试样本;然后,提取每个样本的特征向量,输入到分类器中,得到

预测的编译器版本;最后,将预测值与真实值进行比对,计算准确率、精确率、召回

率、F1值等评价指标。如果测试集上的性能比训练集差很多,说明当前使用的特

征可能过于依赖训练样本的细节,而缺乏一般性。解决方案包括:增加训练样本的

数量和多样性,用更通用的基准测试代码,如SPEC、EEMBC等,覆盖不同应用场

景;人工分析测试集中预测错误的样本,找出其特殊性,对症优化特征工程方法;尝

试其他机器学习模型,特别是更复杂的神经网络结构,用其强大的表征学习能力自

动提取高阶特征;在模型训练中使用正则化技术,如L1/L2范数惩罚、Dropout、

EarlyStopping等,控制模型复杂度,降低过拟合风险。总之,要遵循"用训练样本学

习,用验证样本调参,用测试样本评估"的机器学习流程,做到训练、验证、测试集

的分布一致,循环迭代优化特征和模型,不断增强分类器的泛化性能。

问题4：提高判别函数性能的建议

1. 特征工程：进一步分析编译结果，寻找更多有用的特征。
2. 算法优化：考虑使用更先进的机器学习算法来提高判别函数的性能。
3. 数据集扩充：增加更多的编译结果数据，以提高模型的泛化能力。
4. 参数调优：细致调整模型参数，进行交叉验证以避免过拟合。
5. 代码分析工具：使用或开发更精细的代码分析工具来提高特征提取的准确性。

D题-音板的振动模态分析与参数识别47页高质量论文＋代码＋无水印照片！！

简单麦麦https://www.jdmm.cc/file/2710615/

 

本文针对音板振动建模与参数识别的一系列问题,采用了多种数学建模方法和求解算法,对相关问题进行了深入分析和求解。问题1的 Kirchhoff-Love 均质薄板振动模型：我们首先建立了基于Kirchhoff-Love薄板理论的均质薄板振动模型,该模型采用了垂直于中面的直线保持直线、厚度保持不变、法向应力可忽略不计等假设。在此基础上,我们得到了描述薄板自由振动的偏微分方程组。对于具有自由边界条件的方形薄板,我们还建立了相应的边界条件方程。为了求解该振动模型,我们采用了Ritz方法。

问题2的非均质薄板振动模型： 针对问题2,我们在Kirchhoff-Love理论的基础上,进一步建立了考虑几何非均匀性的非均质薄板振动模型。该模型引入了位置相关的材料参数(密度、弹性模量、泊松比)和几何参数(厚度、弯曲角),以更准确地描述薄板的振动行为。为了求解非均质薄板振动模型,我们提出了基于分片多项式插值的算法。具体来说,我们将整个平面区域划分为若干单元,在每个单元内采用多项式函数对厚度和弯曲角分布进行拟合。最后采用Ritz法或Galerkin法求解。

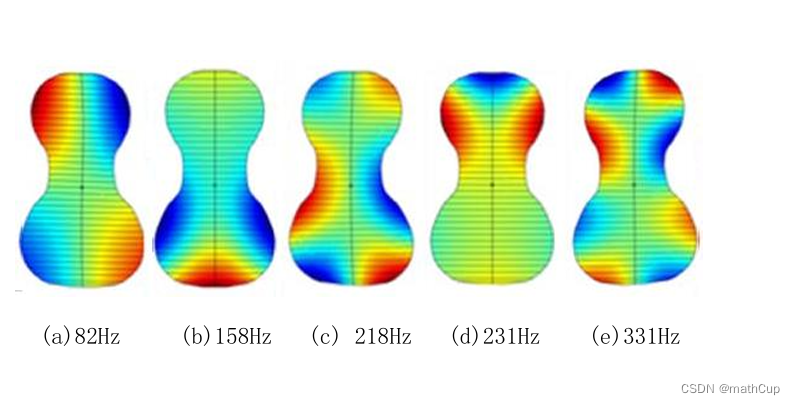
问题3的分离变量法振动模型：针对问题3给出的非均质音板振动信息,我们建立了基于分离变量法的振动模型。该模型将音板的振动位移表示为时间函数和空间振型函数的乘积形式,大大简化了问题的复杂性。为了描述附件提供的5个振型函数$\varphi_j(x,y)$,我们采用了傅里叶级数展开的方法。

问题4的参数识别模型：针对问题4,我们建立了基于非均质音板振动理论的参数识别模型。该模型将密度、杨氏模量、泊松比和厚度等位置相关参数作为待识别对象,目标是确定满足给定振型信息的参数分布。

通过合理选择和扩展这些模型,我们不仅能够有效地求解音板振动问题,还可以深入理解影响振动行为的关键因素,为实际音乐乐器的设计和制造提供重要参考。

关键词：Kirchhoff-Love理论； 振动模型；Ritz 法求解算法； 频率； 音板问题一的分析

对于问题1，我们需要先①建立物理模型和边界条件，确定音板的几何形状（方形均质板）和边界条件（自由边界）。②根据物理模型，建立描述音板振动的偏微分方程，并将边界条件应用于方程中。然后，通过数值方法（如有限元分析）求解该方程，得到不同材质音板的振动模态频率和振型。③搜集各种材料（云杉木材、金属、高新复合材料、新型材料）的振动力学参数，如密度、弹性模量、泊松比等。@b站珞珈山水1 q群476179473④使用收集到的材料参数，计算每种材质音板的振动模态，并对比它们在2000赫兹频率范围内的频率和振型差异。分析这些差异对乐器音色的潜在影响。

问题二的分析

问题2在问题1的基础上,增加了薄板几何非均匀性这一新的关键因素。我们需要建立考虑厚度非均匀和弯曲度分布的非均质薄板振动模型,并采用分片多项式插值算法进行求解。这使得原有的数学模型更加复杂,需要我们具备扎实的建模功底和数值分析技能。首先需要明确任务：选择一种特定的云杉木材来制作一块具有非均匀厚度和一定弯曲度的薄音板，并建立相应的振动数学模型，计算小提琴形状的音板在2000赫兹频率范围内相应振动模态的频率和振型。

该问题与问题1的区别在于，考虑了非均匀厚度、弯曲度、具体的乐器形状。可以在第一问的基础上进行细化和改动。