入门内容
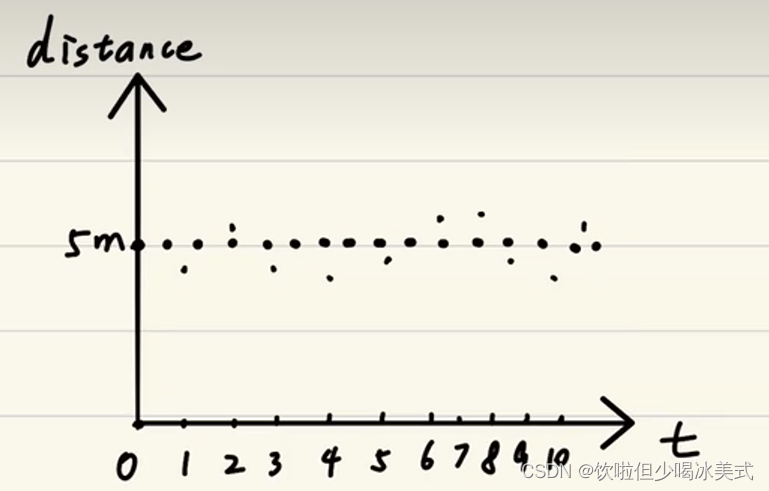
假如有个超声波,它传回的数据是这样的,这样的数据是用不了的
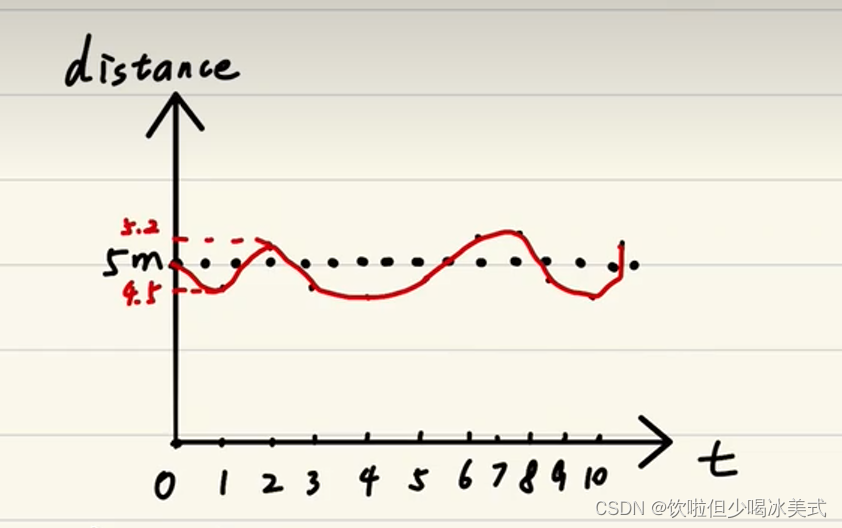
我们想要的是稳定的数据
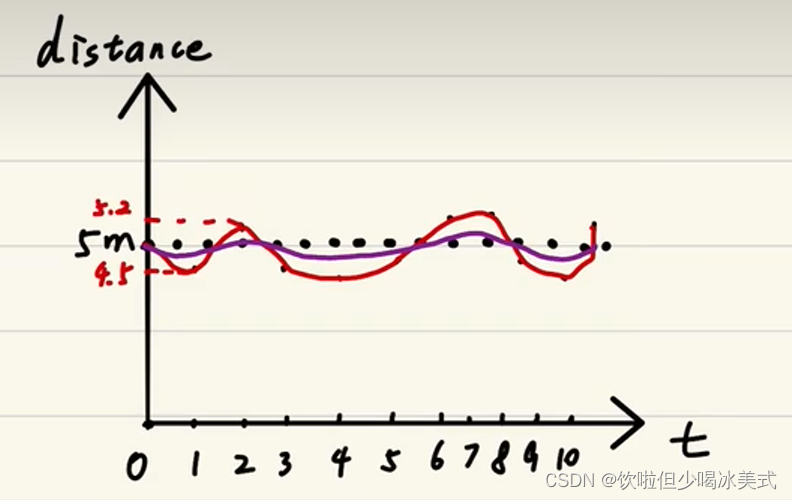
此时我们引入滤波,把里面的噪声去掉,使得数据更平滑
适用系统:
符合两个特质:线性和高斯。 也叫线性高斯系统
什么是线性?
满足两个特性:叠加性和齐次性
叠加型:
假如有两个输入,最后得到一个输出

等价于,总输出是y,由另外两个输出合起来,两个输出对应的输入是x1和x2
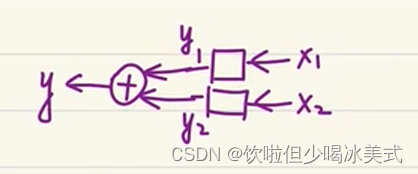
那么从方程理解

齐次性:
x增大k倍,y也增大k倍

高斯:
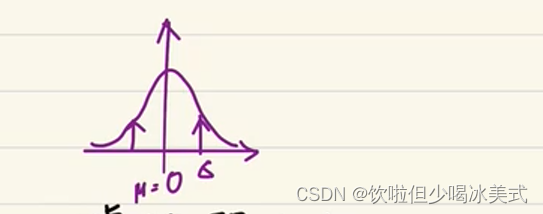
噪声满足正态分布
正态分布就是假如均值为零,它的方差对应着sigma
从宏观来看,卡尔曼滤波就是加权
理想状态: 信号 x 1 + 噪声 x 0
从信号处理的角度来看,类比于低通滤波,低频信号权值为1,高频噪声取值为0
卡尔曼滤波就是有一个估计值和观测值,让你选择它们的权重,融合在一起就是最佳的修正值

进阶内容
状态空间表达式
状态方程
x是状态值,k是当前,k-1是上一个时刻状态,u为输入,w是过程造成(也叫误差)

观测方程
y是观察量,v是观测噪声(传感器自身的误差)

高斯分布
均值和方差
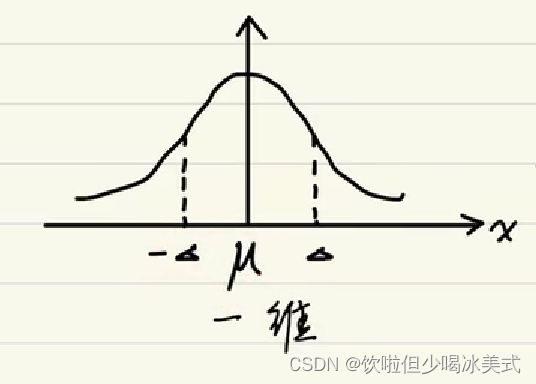
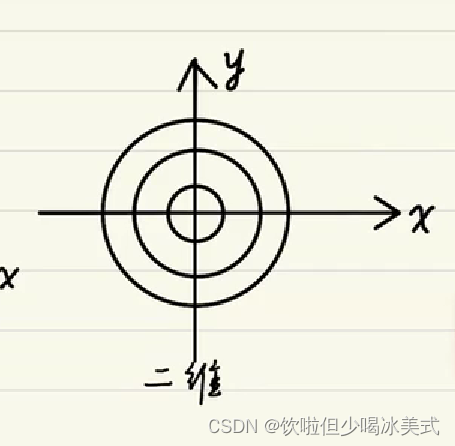

参数分析
主要就是调Q和R
卡尔曼直观图解
最优估计值也叫修正值或者后验估计值
这个是上一时刻的最优估计值,就是卡尔曼滤波最终输出的值
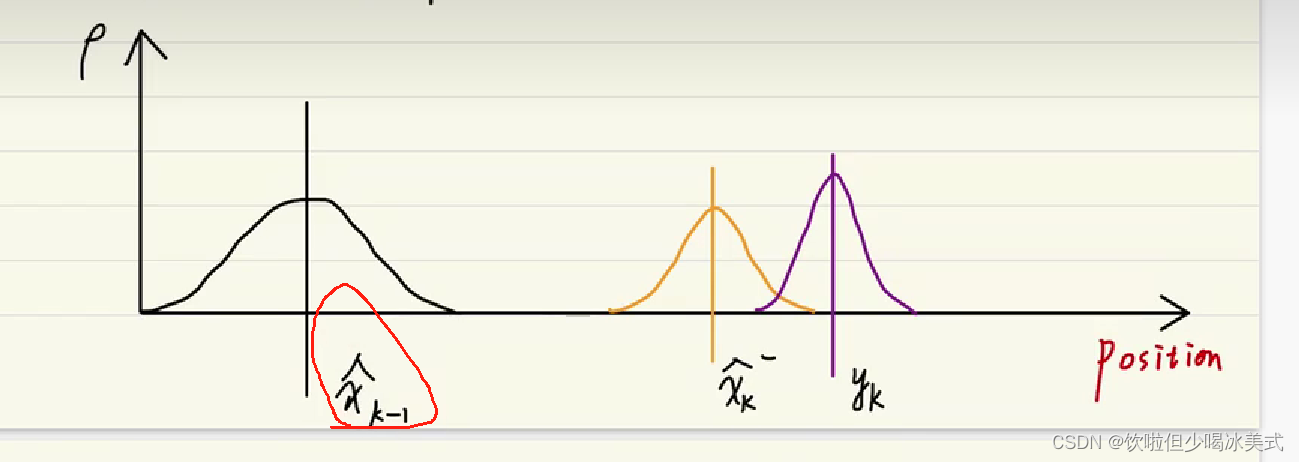
先验估计值
这个值是基于上一时刻的最优估计值估计出来的一个当前估计值
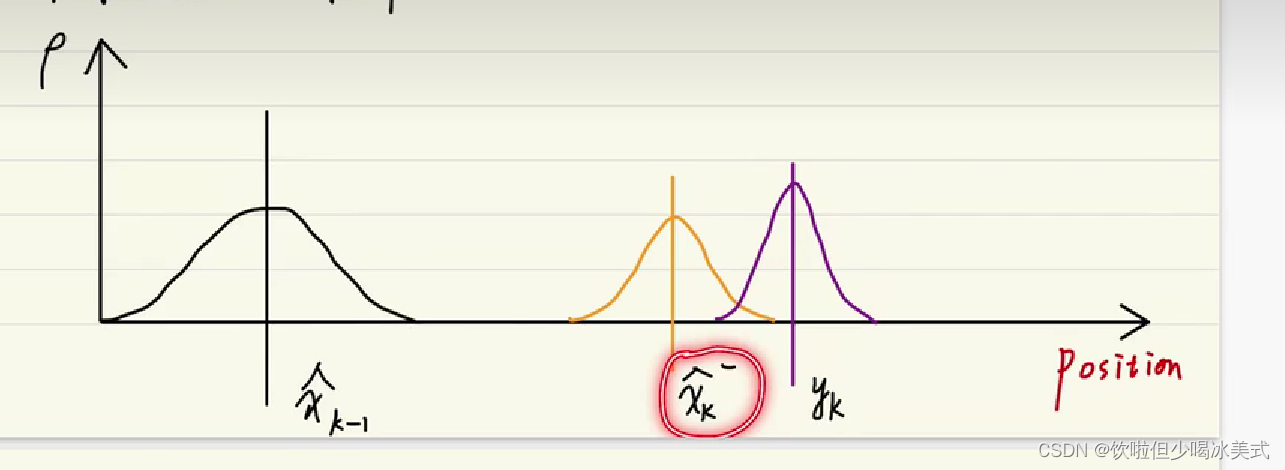
当前时刻的观测值,也就是传感器直接测量出来的值
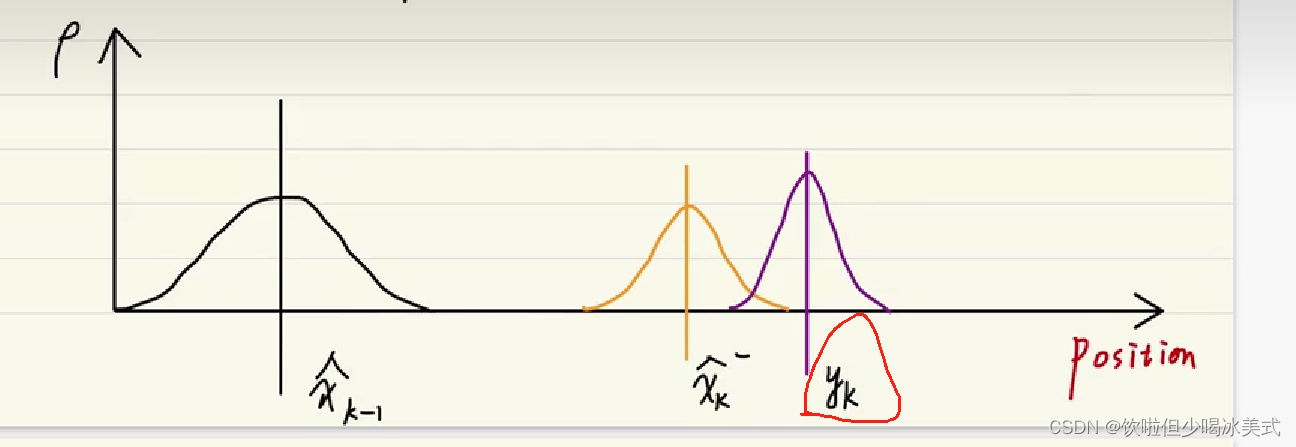
缺一个值,就是当前时刻的最优估计值。大概在这里
滤波次数过多的时候就会趋于一个稳定状态,它的方差自然会越来越小好
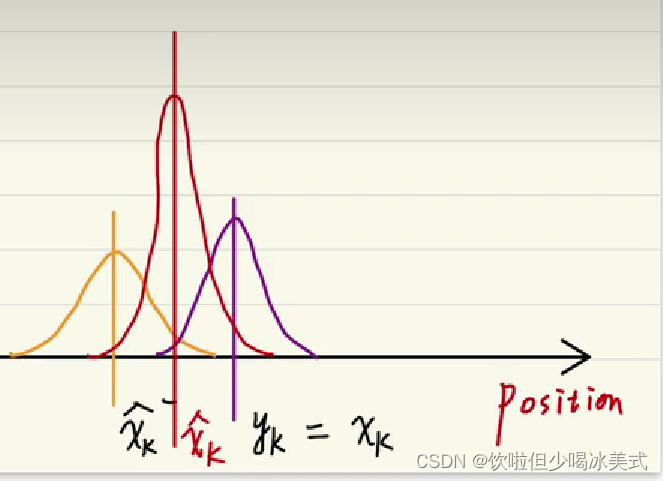
当前估计值与当前观测值的交集

卡尔曼公式理解:
实现过程:用上一次的最优结果预测当前的值
同时使用观测值修正当前值,得到最优结果

import numpy as np
def kalman_filter(observed_data, initial_state_estimate, initial_covariance_estimate, transition_matrix, observation_matrix, process_noise_covariance, observation_noise_covariance):
# 初始化变量
state_estimate = initial_state_estimate # 状态估计
covariance_estimate = initial_covariance_estimate # 协方差估计
# 遍历观测数据
for observation in observed_data:
# 预测步骤
predicted_state_estimate = np.dot(transition_matrix, state_estimate) # 预测状态估计
predicted_covariance_estimate = np.dot(np.dot(transition_matrix, covariance_estimate), transition_matrix.T) + process_noise_covariance # 预测协方差估计
# 更新步骤
innovation = observation - np.dot(observation_matrix, predicted_state_estimate) # 创新
innovation_covariance = np.dot(np.dot(observation_matrix, predicted_covariance_estimate), observation_matrix.T) + observation_noise_covariance # 创新协方差
kalman_gain = np.dot(np.dot(predicted_covariance_estimate, observation_matrix.T), np.linalg.inv(innovation_covariance)) # 卡尔曼增益
state_estimate = predicted_state_estimate + np.dot(kalman_gain, innovation) # 更新状态估计
covariance_estimate = np.dot((np.eye(len(state_estimate)) - np.dot(kalman_gain, observation_matrix)), predicted_covariance_estimate) # 更新协方差估计
return state_estimate, covariance_estimate
# 示例用法
observed_data = np.array([1.2, 1.3, 1.4, 1.5]) # 观测测量
initial_state_estimate = np.array([1.0, 0.0]) # 初始状态猜测
initial_covariance_estimate = np.eye(2) # 初始协方差猜测
transition_matrix = np.array([[1.0, 1.0], [0.0, 1.0]]) # 状态转移矩阵
observation_matrix = np.array([[1.0, 0.0]]) # 观测矩阵
process_noise_covariance = np.eye(2) * 0.01 # 过程噪声协方差
observation_noise_covariance = np.array([[0.1]]) # 观测噪声协方差
state_estimate, covariance_estimate = kalman_filter(observed_data, initial_state_estimate, initial_covariance_estimate, transition_matrix, observation_matrix, process_noise_covariance, observation_noise_covariance)
print("最终状态估计:", state_estimate)
print("最终协方差估计:", covariance_estimate)